
Wetenschap
Wat is een foutenmarge? Deze statistische tool kan u helpen inzicht te krijgen in vaccinproeven en politieke opiniepeilingen
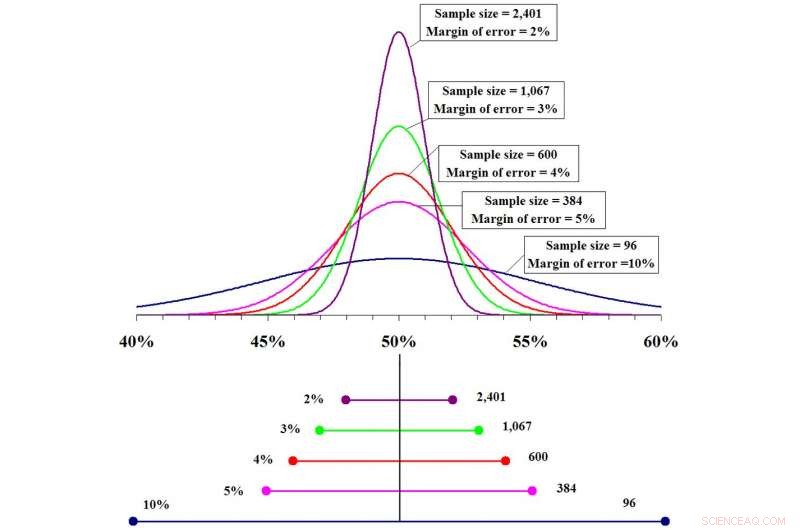
Hoe groter de steekproefomvang, hoe nauwkeuriger de voorspelling en hoe kleiner de foutmarge. Krediet:Fadethree via Wikimedia Commons
In het laatste jaar, statistieken zijn ongewoon belangrijk in het nieuws. Hoe nauwkeurig is de COVID-19-test die u of anderen gebruiken? Hoe weten onderzoekers de effectiviteit van nieuwe therapieën voor COVID-19-patiënten? Hoe kunnen televisiezenders de verkiezingsuitslag voorspellen lang voordat alle stemmen zijn geteld?
Elk van deze vragen brengt enige onzekerheid met zich mee, maar het is nog steeds mogelijk om nauwkeurige voorspellingen te doen zolang die onzekerheid wordt begrepen. Een hulpmiddel dat statistici gebruiken om onzekerheid te kwantificeren, wordt de foutenmarge genoemd.
Beperkte gegevens
Ik ben een statisticus, en een deel van mijn werk is om gevolgtrekkingen en voorspellingen te doen. Met onbeperkte tijd en geld, Ik zou eenvoudig de hele groep mensen waarin ik geïnteresseerd ben kunnen testen of onderzoeken om de vraag in gedachten te evalueren en het exacte antwoord te vinden. Bijvoorbeeld, om het COVID-19-infectiepercentage in de VS te achterhalen, Ik zou gewoon de hele Amerikaanse bevolking kunnen testen. Echter, in de echte wereld, je hebt nooit toegang tot 100% van een populatie.
In plaats daarvan, statistici bemonsteren een klein deel van de bevolking en bouwen een model om een voorspelling te doen. Met behulp van statistische theorie, dat resultaat van de steekproef wordt geëxtrapoleerd om de hele populatie weer te geven.
Ideaal, een goede steekproef moet representatief zijn voor de totale populatie, inclusief geslacht, raciale diversiteit, sociaaleconomische diversiteit, levensstijlpatronen en andere demografische maatstaven. Hoe groter de steekproef, hoe meer het lijkt op de echte populatie, en met een grotere steekproef, hoe zelfverzekerder statistici worden in hun voorspellingen. Maar er zal altijd enige onzekerheid zijn.
Onzekerheid kwantificeren
Neem de ontwikkeling van medicijnen, bijvoorbeeld. Het is altijd waar om te voorspellen dat een nieuw medicijn ergens tussen de 0% en 100% effectief zal zijn voor iedereen op aarde. Maar dat is geen erg bruikbare voorspelling. Het is de taak van een statisticus om dat bereik te verkleinen tot iets nuttigers. Statistici noemen dit bereik meestal een betrouwbaarheidsinterval, en het is het bereik van voorspellingen waarbinnen statistici er zeer zeker van zijn dat het werkelijke aantal zal worden gevonden.
Als een medicijn werd getest op 10 personen en zeven van hen vonden het effectief, de geschatte werkzaamheid van het geneesmiddel is 70%. Maar aangezien het doel is om de werkzaamheid in de hele populatie te voorspellen, statistici moeten rekening houden met de onzekerheid van het testen van slechts 10 mensen.
Betrouwbaarheidsintervallen worden berekend met behulp van een wiskundige formule die de steekproefomvang omvat, het bereik van de antwoorden en de wetten van waarschijnlijkheid. In dit voorbeeld, het betrouwbaarheidsinterval zou tussen 42% en 98% liggen - een bereik van 56 procentpunten. Na het testen van slechts 10 mensen, je zou met veel vertrouwen kunnen zeggen dat het medicijn effectief is voor tussen de 42% en 98% van de mensen in de hele bevolking.
Als je het betrouwbaarheidsinterval door de helft deelt, je krijgt de foutenmarge - in dit geval, 28%. Hoe groter de foutmarge, hoe minder nauwkeurig de voorspelling. Hoe kleiner de foutmarge, hoe nauwkeuriger de voorspelling. Een foutenmarge van bijna 30% is nog steeds een behoorlijk breed bereik.
Echter, stel je voor dat de onderzoekers dit nieuwe medicijn hebben getest op 1, 000 mensen in plaats van 10 en het was effectief bij 700 van hen. De geschatte werkzaamheid van het geneesmiddel zal nog steeds rond de 70% zijn, toch is deze voorspelling veel nauwkeuriger. Het betrouwbaarheidsinterval voor de grotere steekproef zal tussen 67% en 73% liggen met een foutenmarge van 3%. Je zou kunnen zeggen dat dit medicijn naar verwachting 70% effectief zal zijn, plus of min 3%, voor de hele bevolking.
Statistici zouden graag met 100% nauwkeurigheid het succes of falen van een nieuw medicijn of de exacte resultaten van een verkiezing kunnen voorspellen. Echter, dit is niet mogelijk. Er is altijd wat onzekerheid, en de foutenmarge is wat die onzekerheid kwantificeert; het moet worden overwogen bij het bekijken van resultaten. Vooral, de foutenmarge definieert het bereik van voorspellingen waarbinnen statistici er zeker van zijn dat het werkelijke aantal zal worden gevonden. Een aanvaardbare foutenmarge is een kwestie van oordeel op basis van de mate van nauwkeurigheid die vereist is in de te trekken conclusies.
Dit artikel is opnieuw gepubliceerd vanuit The Conversation onder een Creative Commons-licentie. Lees het originele artikel. 
 Onderzoekers onthullen de aard van het bodemwater en de faseovergang ervan
Onderzoekers onthullen de aard van het bodemwater en de faseovergang ervan Oplossen van molecuulinformatie in dynamisch lipidemembraan met meta-oppervlakken
Oplossen van molecuulinformatie in dynamisch lipidemembraan met meta-oppervlakken Copycat-cellen beschikken over nieuwe communicatiekrachten
Copycat-cellen beschikken over nieuwe communicatiekrachten De puzzel voor het ontwerpen van medicijnen voltooien
De puzzel voor het ontwerpen van medicijnen voltooien Hoe werken infrarood-thermometers?
Hoe werken infrarood-thermometers?
Hoofdlijnen
- Is er verteld dat je te gevoelig bent? Je zou een empaat kunnen zijn
- Hoe de bacteriegroei in petrischalen te meten
- Hoe een diercelmodel te maken
- Onderzoekers ontdekken wat er bij libellen op het menu staat
- De ecologische kosten van oorlog:conflict een consequente moordenaar van Afrikaanse megafauna
- De gemiddelde levensduur van skeletspiercellen
- Pareidolie:waarom we in bijna alles gezichten zien
- De hectische 24-uurs inspanning om een bedreigde, verweesde vleermuis
- Lignine-afval aangepast voor industrieel gebruik van bio-olie
- Wat als we geen fossiele brandstoffen meer zouden hebben?

- Wat is de militaire (slimme) brandstofcel?

- Langzaam fietsen is niet alleen voor de lol - het is essentieel voor veel stadswerkers

- De impact van klimaatverandering op taalverlies

- Racisme in het voetbal:nieuw onderzoek toont aan dat de media zwarte mannen anders behandelen dan blanke mannen

 Wat veroorzaakte de scheiding van de aarde in lagen?
Wat veroorzaakte de scheiding van de aarde in lagen?  Sidewinder Snake Facts
Sidewinder Snake Facts Een enkelbladige grafeen pn-overgang met twee bovenste poorten
Een enkelbladige grafeen pn-overgang met twee bovenste poorten Vijf olifanten gedood door trein in India
Vijf olifanten gedood door trein in India Wetenschappelijke methode voor vulkaanwetenschappelijke projecten
Wetenschappelijke methode voor vulkaanwetenschappelijke projecten Waterdiefstal een groeiend probleem in het steeds droger wordende Spanje
Waterdiefstal een groeiend probleem in het steeds droger wordende Spanje HD-video van de maan in bijna realtime
HD-video van de maan in bijna realtime Fossiele vondsten geven aanwijzingen over vliegende reptielen in de Sahara 100 miljoen jaar geleden
Fossiele vondsten geven aanwijzingen over vliegende reptielen in de Sahara 100 miljoen jaar geleden
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | German | Dutch | Danish | Norway | Swedish |

-
Wetenschap © https://nl.scienceaq.com

