
Wetenschap
De simpele reden waarom een virale wiskundige vergelijking het internet overrompelde

Waren verschillende manieren om de volgorde van bewerkingen aan te leren verantwoordelijk voor verwarring? Tegoed:Shutterstock
Al zo'n tien jaar houden wiskundigen en wiskundedocenten zich bezig met een bepaald debat dat geworteld is in schoolwiskunde en dat geen tekenen van afname vertoont.
Het debat, behandeld door Slate, Popular Mechanics , The New York Times en vele andere verkooppunten, is gericht op een vergelijking die zo 'viraal' ging dat het uiteindelijk op één hoop werd gegooid met andere verschijnselen die het internet hebben 'gebroken' of 'verdeeld'.
Als u zich nog moet wegen, zou dit een goed moment zijn om te zien waar u staat. Beantwoord alstublieft het volgende:
8÷2(2+2)=?
Als je zoals de meesten bent, was je antwoord 16 en je bent verbijsterd dat iemand anders een ander antwoord kan vinden. Tenzij, dat wil zeggen, je bent zoals de meeste anderen en je antwoord was 1 en je bent net zo in de war over het op een andere manier zien. Vrees niet, in wat volgt, zullen we het definitieve antwoord op deze vraag uitleggen - en waarom de manier waarop de vergelijking is geschreven, moet worden verboden.
Onze interesse was gewekt omdat we onderzoek hebben gedaan naar conventies over het volgen van de volgorde van bewerkingen - een opeenvolging van stappen die worden genomen wanneer we worden geconfronteerd met een wiskundige vergelijking - en we waren een beetje in de war met waar alle ophef over ging.
Het antwoord is duidelijk…
Twee haalbare antwoorden op één wiskundeprobleem? Nou, als er één ding is dat we ons allemaal herinneren van de wiskundeles:dat kan niet kloppen!
Veel thema's kwamen naar voren uit de overvloed aan artikelen waarin werd uitgelegd hoe en waarom deze "vergelijking" het internet brak. Het invoeren van de uitdrukking op rekenmachines, waarvan sommige zijn geprogrammeerd om een bepaalde volgorde van bewerkingen te respecteren, werd veel besproken.
Anderen, die zich een beetje indekken, suggereren dat beide antwoorden correct zijn (wat belachelijk is).
Het meest dominante thema was eenvoudigweg gericht op de uitvoering van de volgorde van bewerkingen volgens verschillende acroniemen. Sommige commentatoren zeiden dat de misverstanden van mensen werden toegeschreven aan een onjuiste interpretatie van het uit het hoofd geleerde acroniem dat in verschillende landen werd geleerd om de volgorde van bewerkingen te onthouden, zoals PEMDAS, soms gebruikt in de Verenigde Staten:PEMDAS verwijst naar het toepassen van haakjes, exponenten, vermenigvuldigen, delen, optellen en aftrekken.
Een persoon die deze volgorde volgt, zou 8÷2(2+2) 8÷2(4) hebben, dankzij het beginnen met haakjes. Dan wordt 8÷2(4) 8÷8 omdat er geen exponenten zijn, en "M" staat voor vermenigvuldiging, dus vermenigvuldigen ze 2 met 4. Ten slotte, volgens de "D" voor deling, krijgen ze 8÷8=1.
Daarentegen kunnen Canadezen worden geleerd BEDMAS te onthouden, wat staat voor het toepassen van haakjes, exponenten, delen, vermenigvuldigen, optellen en aftrekken. Iemand die deze volgorde volgt, zou 8÷2(2+2) 8÷2(4) laten worden door te beginnen met haakjes (hetzelfde als haakjes). Dan wordt 8÷2(4) 4(4) omdat (er zijn geen exponenten) en "D" staat voor delen. Ten slotte, volgens de "M" voor vermenigvuldiging, 4 (4) =16.
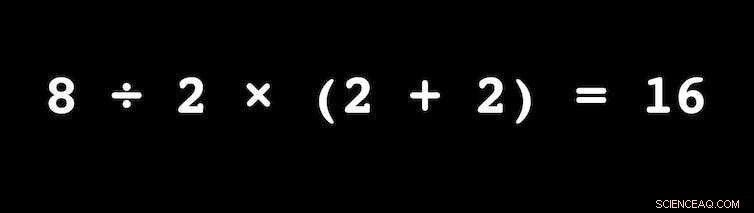
Als het probleem correct was gepresenteerd als 8 ÷ 2 × (2 + 2) =?, zou er geen verhitte discussie zijn. Krediet:Egan J. Chernoff, auteur verstrekt
Sla het vermenigvuldigingssymbool niet weg
Voor ons is de uitdrukking 8÷2(2+2) syntactisch onjuist.
De sleutel tot het debat, zo stellen we, is dat het vermenigvuldigingssymbool vóór de haakjes is weggelaten.
Een dergelijke omissie is een conventie in de algebra. In de algebra schrijven we bijvoorbeeld 2x of 3a, wat 2 × x of 3 × a betekent. Wanneer letters worden gebruikt voor variabelen of constanten, wordt het vermenigvuldigingsteken weggelaten. Beschouw de beroemde vergelijking e=mc 2, wat de berekening van energie suggereert als e=m×c 2.
De echte reden dat 8 ÷ 2 (2 + 2) het internet brak, komt voort uit de praktijk om het vermenigvuldigingssymbool weg te laten, wat ongepast naar de rekenkunde van de algebra werd gebracht.
Ongepaste prioriteit
Met andere woorden, als de uitdrukking correct was "gespeld", dat wil zeggen, gepresenteerd als "8 ÷ 2 × (2 + 2) =? ", zou er geen viral gaan, geen dualiteit, geen kapot internet, geen verhitte debatten. Niet leuk!
Uiteindelijk leidt het weglaten van het vermenigvuldigingssymbool tot ongepaste prioriteit voor vermenigvuldiging. Alle commentatoren waren het erover eens dat het toevoegen van de termen tussen haakjes of haakjes de juiste eerste stap was. Maar er ontstond verwarring gezien de nabijheid van 2 tot (4) ten opzichte van 8 in 8÷2(4).
We willen dat het bekend is dat het schrijven van 2(4) om te verwijzen naar vermenigvuldiging ongepast is, maar we begrijpen dat het altijd en overal wordt gedaan.
Mooi symbool voor vermenigvuldiging
Er is een heel mooi symbool voor vermenigvuldigen, dus laten we het gebruiken:2 × 4. Mocht je geen fan zijn, dan zijn er andere symbolen, zoals 2•4. Gebruik een van beide, naar eigen goeddunken, maar laat het niet weg.
Als zodanig, voor de goede orde, het debat over één tegen 16 is nu voorbij! Het antwoord is 16. Zaak gesloten. Bovendien had er in de eerste plaats nooit echt een debat mogen plaatsvinden. + Verder verkennen
Studie legt uit hoe sommige oudere hersenen achteruitgaan voordat mensen het beseffen
Dit artikel is opnieuw gepubliceerd vanuit The Conversation onder een Creative Commons-licentie. Lees het originele artikel. 
 Hoe groot is een fragment?
Hoe groot is een fragment? Nieuwe sensor detecteert waardevol terbium van zeldzame aardelementen uit niet-traditionele bronnen
Nieuwe sensor detecteert waardevol terbium van zeldzame aardelementen uit niet-traditionele bronnen Nieuwe eiwitstructuren om rationeel medicijnontwerp te ondersteunen
Nieuwe eiwitstructuren om rationeel medicijnontwerp te ondersteunen Een ongebruikelijk molecuul beschermt zenuwcellen tegen degeneratie
Een ongebruikelijk molecuul beschermt zenuwcellen tegen degeneratie Nieuwe beeldvormingstechniek onthult hoe mechanische schade begint op moleculaire schaal
Nieuwe beeldvormingstechniek onthult hoe mechanische schade begint op moleculaire schaal
 Watermeters helpen wetenschappers rivierafvoer te kwantificeren
Watermeters helpen wetenschappers rivierafvoer te kwantificeren NASA vindt kommavorm van tropische storm Wukong
NASA vindt kommavorm van tropische storm Wukong Welk klimaat en weer is te vinden in een zoetwatermoeras?
Welk klimaat en weer is te vinden in een zoetwatermoeras?  Grootste massale uitsterving veroorzaakt door de opwarming van de aarde waardoor oceaandieren naar adem snakken
Grootste massale uitsterving veroorzaakt door de opwarming van de aarde waardoor oceaandieren naar adem snakken Explainer:Waarom het maanden duurt om enkele bosbranden te bedwingen
Explainer:Waarom het maanden duurt om enkele bosbranden te bedwingen
Hoofdlijnen
- Studie vindt nieuwe manier om radioactieve sites op te ruimen, bescherming van radiotherapiepatiënten, astronauten
- Bioom: definitie, types, kenmerken en voorbeelden
- Onderzoekers ontdekken nieuwe overspraak tussen fytohormonen ethyleen en auxine
- Wat zijn de functies van mRNA & tRNA?
- Saharastof:het goede,
- Chinese fossiele eieren tonen achteruitgang van dinosauriërs voordat ze uitstierven
- Vitamine E-ontdekking in maïs kan leiden tot meer voedzame gewassen
- Grootte is belangrijk - hoe trips hun partners kiezen
- Slimme technologie helpt bij onderzoek naar een nationaal belangrijke zeevogelkolonie
- Evolutie:hoe de theorie inspireert tot een nieuwe manier om taal te begrijpen

- Betaald worden om de planeet te redden: uw gids voor groene banen

- Dramatische verandering in oude nomadische diëten valt samen met uitbreiding van netwerken in Eurazië

- Onderzoek biedt een nieuwe manier om de public relations van een organisatie te beoordelen

- De 10 zwaarste gebouwen ooit verplaatst

 Kleine ster werpt licht op jonge planeten
Kleine ster werpt licht op jonge planeten We kunnen het milieu duurzaam beheren, maar we moeten eraan werken
We kunnen het milieu duurzaam beheren, maar we moeten eraan werken Lars Bildsten wint 2017 Dannie Heineman Prize for Astrophysics
Lars Bildsten wint 2017 Dannie Heineman Prize for Astrophysics Quota krijgen meer vrouwen in besturen en zorgen voor verandering van binnenuit
Quota krijgen meer vrouwen in besturen en zorgen voor verandering van binnenuit Afbeelding:NASA ziet nog steeds branden in het zuidoosten van de VS
Afbeelding:NASA ziet nog steeds branden in het zuidoosten van de VS Trucs om de polyatomic Ions
Trucs om de polyatomic Ions Noem drie soorten aseksuele reproductie
Noem drie soorten aseksuele reproductie  Na de lekkage van Deepwater Horizon:welke dieren hebben de ramp doorstaan?
Na de lekkage van Deepwater Horizon:welke dieren hebben de ramp doorstaan?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

