
Wetenschap
Wiskundigen creëren een methode om de eigenschappen van poreuze materialen te bestuderen
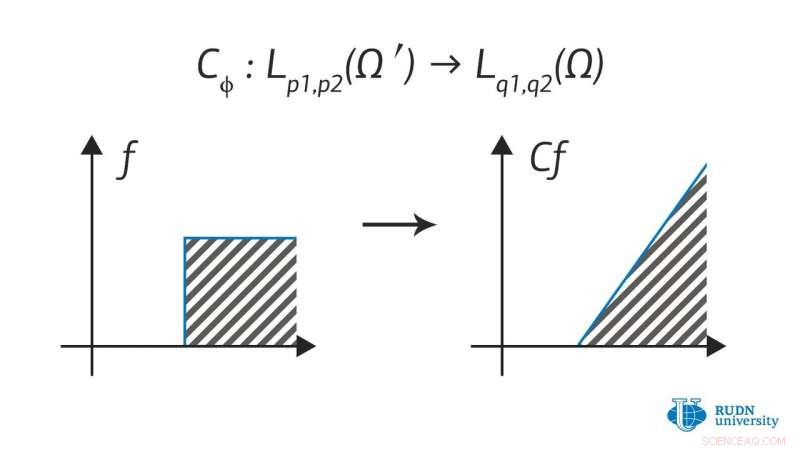
Krediet:RUDN University
Wiskundigen van de RUDN University hebben de eigenschappen van compositorische operatoren bestudeerd in ruimten met gemengde Lebesgue-normen. Hun werk zal helpen bij het beschrijven van de diffusie van vloeistoffen in materialen met scheuren en in poreuze materialen. Dergelijke ruimten zijn ook nuttig voor het verkrijgen van schattingen voor oplossingen voor de Navier-Stokes-vergelijking. Het artikel is gepubliceerd in Wiskundige notities .
De moderne wetenschap van partiële differentiaalvergelijkingen heeft haar eigen theorie:de taal van de functionele analyse. Studies van functieruimten waarin oplossingen voor vergelijkingen worden gezocht, begonnen in de 19e eeuw en zijn tot op heden voortgezet. Aanvankelijk, wiskundigen leerden de Fourier-theorie toe te passen op oplossingen voor de eenvoudigste lineaire partiële differentiaalvergelijkingen, bestudeerde vervolgens Banach- en Hilbertruimten, evenals ruimten van gegeneraliseerde functies, wat in wezen de taal van de kwantummechanica is.
Rond het midden van de 20e eeuw, Sobolev-ruimten werden ontdekt; deze bezetten nu een van de centrale posities in de theorie van partiële differentiaalvergelijkingen. In de komende 50 jaar zal ze hielpen wiskundigen bij het vinden van veel oplossingen voor toegepaste problemen die niet in gewone functionele ruimtes te vinden zijn.
Dichter bij het begin van de 21e eeuw, het werd noodzakelijk om nieuwe methoden te vinden om niet-lineaire partiële differentiaalvergelijkingen te bestuderen, dus computationele wiskunde en de theorie van integreerbare systemen werden ontwikkeld. Echter, methoden uit deze velden bleken te eng gericht te zijn, en de noodzaak om de taal te ontwikkelen is er nog steeds.
Lebesgue-ruimten met gemengde normen zijn soms meer universele en flexibele objecten. Deze ruimten worden als volgt bepaald:In de ruimte van functies in verschillende variabelen, de norm definiëren door de Lebesgue-norm te herhalen. Ze ontstonden aanvankelijk als een van de generalisaties van Sobolev-ruimten en hebben al veel belangstelling getrokken van theoretici uit verschillende landen van Europa, evenals China, Canada en Rusland.
Nikita Evseev en Alexander Menovshchikov van het Mathematisch Instituut van de RUDN University werken aan een theorie van operatoren voor dergelijke ruimtes, waarmee ze kunnen worden gebruikt in toegepaste problemen die zijn geformuleerd in de taal van partiële differentiaalvergelijkingen. Ze produceerden een flink aantal nieuwe resultaten die de eigenschappen van operatoren op dergelijke ruimtes beschrijven:criteria voor begrensdheid van operatoren, eigenschappen van integrale operatoren, vermenigvuldigingsoperators, compositie-operators, en vele anderen. Ze behaalden ook enkele hulpresultaten die nuttig zijn voor de verdere ontwikkeling van dit vakgebied.
"Onze methoden en resultaten, we geloven, kan worden toegepast op evolutionaire problemen en differentiële problemen op niet-cilindrische regio's. Bijvoorbeeld, in (wiskundige) biologie, waar het oppervlak of het bestudeerde gebied met de tijd verandert, of in de hydrodynamica, voor problemen met een variabele grens, ’ zegt Evseev.
Onderzoek op dit gebied is nuttig voor het bestuderen van de Navier-Stokes-vergelijkingen, een systeem van vergelijkingen die aero- en hydrodynamica beschrijven. Lebesgue-ruimten met gemengde normen maken het mogelijk om oplossingen te evalueren, die, beurtelings, maakt het mogelijk om de afwezigheid van turbulentie te voorspellen, bijvoorbeeld.
De resultaten zullen ook helpen bij het bestuderen van de toegepaste problemen van wiskundige fysica die zich voordoen bij de studie van poreuze materialen en materialen met scheuren. Bijvoorbeeld, het zal mogelijk zijn om het patroon van diffusie en warmteoverdracht in silicagels theoretisch te voorspellen, poreuze bril, verschillende sponzen, en schuim, evenals in sommige bouwmaterialen.
 Een hart-gezond eiwit uit zemelen van graangewassen
Een hart-gezond eiwit uit zemelen van graangewassen Onderzoek haalt de kou weg van ijzige opbouw op vliegtuigen en windturbines
Onderzoek haalt de kou weg van ijzige opbouw op vliegtuigen en windturbines Toekomstige anticonceptiepil voor mannen heeft zijn oorsprong in een pijlgif
Toekomstige anticonceptiepil voor mannen heeft zijn oorsprong in een pijlgif Things Made uit Tungsten
Things Made uit Tungsten  Waarom is het belangrijk om een pH-meter en zijn elektroden tegen een buffer te kalibreren?
Waarom is het belangrijk om een pH-meter en zijn elektroden tegen een buffer te kalibreren?
 NASA vindt windschering bij tropische depressie 16W
NASA vindt windschering bij tropische depressie 16W Puerto Rico onderzoekt uitbraak van ziekte na orkaan
Puerto Rico onderzoekt uitbraak van ziekte na orkaan Nieuw onderzoek suggereert dat wereldwijde herbebossingsinspanningen een langetermijnvisie moeten hebben
Nieuw onderzoek suggereert dat wereldwijde herbebossingsinspanningen een langetermijnvisie moeten hebben Bosbranden verschroeien huizen van de rijken en beroemdheden in Los Angeles
Bosbranden verschroeien huizen van de rijken en beroemdheden in Los Angeles Onverwachte boosdoener:wetlands als bron van methaan
Onverwachte boosdoener:wetlands als bron van methaan
Hoofdlijnen
- Hoe antidepressiva werken
- Diabetesmedicijn helpt bij het repareren van UV-beschadigd DNA in cellen van maankinderen
- Zoogdieren schakelden over op dagactiviteit na uitsterven van dinosauriërs
- Plasmamembraan: definitie, structuur en functie (met diagram)
- Welke organel moet aanwezig zijn in grote aantallen in spiercellen?
- Facilitated Diffusion: Definition, Example & Factors
- Vleermuizen en insecten vechten in de tropen
- Door wetenschap ondersteunde manieren om een nieuwe studie te starten
- Waarom is UV-licht schadelijk?
- Metaal als een hernieuwbare of niet-hernieuwbare bron

- Begrijpen hoe Afrikaans-Australiërs over COVID denken, kan helpen om de berichtgeving over de volksgezondheid op maat te maken

- Robots zijn zeldzaam in de bouwsector,

- Hier is hoe fruit vliegt ooit zou kunnen genezen chronische pijn

- Oefening in een eerstejaars schrijfcursus verhoogt de retentie op breed toegankelijke universiteiten

 Wat is er aan de hand met het mysterieuze Zug-eiland van Detroit?
Wat is er aan de hand met het mysterieuze Zug-eiland van Detroit?  NASA-satellietbeelden vinden Rebekah nu post-tropisch
NASA-satellietbeelden vinden Rebekah nu post-tropisch Hoe een man te onderscheiden van een vrouwelijke blauwe Jay
Hoe een man te onderscheiden van een vrouwelijke blauwe Jay Astronomen onderzoeken pulsar windnevel DA 495
Astronomen onderzoeken pulsar windnevel DA 495 Onderzoekers gebruiken golfgeleiders voor gevoelige proteasemonitoring
Onderzoekers gebruiken golfgeleiders voor gevoelige proteasemonitoring Ontcelde spinazie dient als eetbaar platform voor in het laboratorium gekweekt vlees
Ontcelde spinazie dient als eetbaar platform voor in het laboratorium gekweekt vlees Periodiek systeem:nieuwe versie waarschuwt voor elementen die in gevaar zijn
Periodiek systeem:nieuwe versie waarschuwt voor elementen die in gevaar zijn Wetenschappers bewijzen dat dubbelsterren licht van elkaar reflecteren
Wetenschappers bewijzen dat dubbelsterren licht van elkaar reflecteren
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

