
Wetenschap
De universele schoonheid van de bergen is te zien in grafieken

De bergketens van de aarde hebben dezelfde universele kenmerken. Ze worden zichtbaar wanneer de topografische kaart (hier:de Ligurische Alpen) wordt omgezet in een bergkamkaart. (Bron:IFJ PAN) Krediet:Bron:IFJ PAN
Bergen hebben karakter. De continue zachte, golvende heuvels en brede valleien van de Karpaten, Appalachen of lagere delen van de Alpen contrasteren sterk met de stijgende toppen, rafelige bergkammen en diepe ravijnen van het hoge Tatra-gebergte en de Pyreneeën, welke zijn, beurtelings, anders dan het ontoegankelijke, met sneeuw bedekte reuzen uit de Himalaya of de Andes, langs wiens hellingen lange tongen van gletsjers stromen in plaats van water. Onder deze grote diversiteit, echter, ligt een verrassend vergelijkbare structuur.
Met behulp van grafieken en fractals, wetenschappers van het Instituut voor Kernfysica van de Poolse Academie van Wetenschappen (IFJ PAN) in Krakau keken naar de structuur van de massieven van onze planeet. Zulke uiteenlopende gebieden als de Alpen, de Pyreneeën, de Scandinavische bergen, het Baetische gebergte, de Himalaya, het Andesgebergte, de Appalachen, het Atlasgebergte en de Zuidelijke Alpen gingen allemaal onder het statistische vergrootglas. De analyse, gepresenteerd in de Tijdschrift voor complexe netwerken , resulteerde in een onverwachte observatie. Het blijkt dat er een universele overeenkomst is in de structuur van de massieven van de aarde. Het is te zien in bergketens op alle continenten, ongeacht de grootte van de pieken, hun leeftijd, of zelfs of ze van tektonische of vulkanische oorsprong zijn.
"Het lijkt erop dat het enige dat de verschillende bergketens gemeen hebben, is dat als je ernaar kijkt, je moet echt je hoofd naar achteren buigen. De echte overeenkomst wordt pas zichtbaar als we een eenvoudige topografische kaart van de bergen omzetten in een bergkamkaart, d.w.z. een die de assen van alle richels laat zien, " zegt Dr. Jaroslaw Kwapien (IFJ PAN), en voegt er dan aan toe:"De as van de bergkam is een lijn die langs de top van de bergkam loopt, zodanig dat het terrein aan beide zijden naar beneden valt. Het is dus het tegenovergestelde van de as van een vallei."
Bergruggen zijn geen discrete creaties. Ze smelten samen tot een grote, vertakte structuur, lijkt op een boom:vanaf de hoofdkam ("de stam") zijn er langere of kortere zijruggen van de eerste orde ("takken"), daaruit ontstaan zijruggen van de tweede orde, en van deze volgende keer op keer. Het geheel heeft een duidelijk hiërarchische structuur en het aantal graden van complexiteit hangt af van de grootte van het met bergen bedekte gebied en kan zelfs enkele tientallen bereiken. Structuren van dit type worden gepresenteerd in de vorm van verschillende grafieken. Bijvoorbeeld, elke nok van een gegeven massief kan worden behandeld als een knoop. Twee knopen zijn verbonden door lijnen (randen van de grafiek) wanneer de corresponderende ruggen ook verbonden zijn. In dit soort grafieken sommige knooppunten zijn verbonden met veel knooppunten, terwijl anderen slechts met enkelen verbonden zijn.
Grafieken die voor verschillende massieven zijn gemaakt, hebben verschillende structuren (topologie). Een manier om deze te bestuderen is de knooppuntgraadverdeling, met informatie over het aantal knopen van een bepaalde graad. In typische distributies, grote waarden verschijnen op knooppunten van een lage graad, omdat ze het talrijkst zijn. Er zijn meestal niet veel knooppunten van hoge graad - hubs. In het geval van bergen, de belangrijkste hub, meestal overeenkomend met de langste bergkam van de bestudeerde bergketen, heeft een graad van enkele duizenden. Naven van de tweede orde, d.w.z. zijruggen van de hoofdkam, hebben graden van enkele honderden. De meest talrijke zijn knooppunten met een graad van één. Dit kunnen er zelfs enkele honderdduizenden zijn.
"De knooppuntgraadverdeling van de ruggen blijkt van een machtswet-karakter te zijn. Dit betekent dat het aantal knooppunten van een bepaalde graad en, bijvoorbeeld, het aantal knopen met een graad die half zo groot is, staat in een constante relatie, ongeacht de gekozen graad. Elk fragment van de verdeling verhoogd met een bepaalde constante factor ziet eruit als een geheel, wat betekent dat er geen schaal wordt onderscheiden, " zegt dr. Kwapien.
Machtswetverdelingen worden gevonden in grafieken die systemen voorstellen die in de natuur voorkomen (bijvoorbeeld bij het bestuderen van de verbanden tussen eiwitten en enzymen in een levende cel), evenals in onze eigen activiteiten (zoals citaten van wetenschappelijke artikelen, de medewerking van acteurs in films, de buurt van woorden in teksten, koppelingen tussen websites). Ze beschrijven vaak zelf-gelijken, fractale structuren. Een van de modelvoorbeelden van natuurlijke fractals zijn bergen. Hun computermodellen worden zelfs gegenereerd door algoritmen die gebruik maken van fractale geometrie, dus de machtswet-topologie van nokgrafieken zou niemand moeten verbazen. Echter, de waarde van de machtsexponent bleek wel een verrassing.
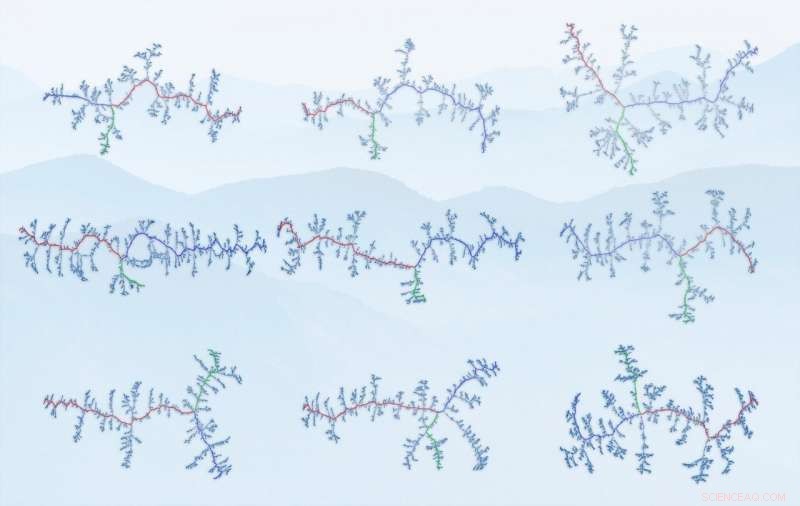
Ridge grafieken van de bestudeerde bergketens. De knooppunten hier zijn de snijpunten van richels, de randen - de ribbels zelf. Van linksboven:Alpen, Baetische bergen, Pyreneeën, Scandinavische bergen, Himalaya (deel), Zuidelijke Alpen, Appalachen, Andes (deel), Atlasgebergte. (Bron:IFJ PAN) Krediet:Bron:IFJ PAN
"Ongeacht het soort bergen, de exponent van de machtswetverdeling nam waarden aan over een zeer smal bereik rond het getal 5/3. Als we rekening houden met de nauwkeurigheid van onze methodologie, dit smalle bereik van waarden kan zelfs betekenen dat de exponenten in elk onderzocht geval hetzelfde waren, " merkt dr. Kwapien op.
De waargenomen homogeniteit komt voort uit het feit dat in elk deel van onze planeet de belangrijkste mechanismen die verantwoordelijk zijn voor bergsculptuur in wezen hetzelfde zijn. Tektonische of vulkanische bewegingen zijn nodig om het terrein te verhogen, maar de belangrijkste vormgevende factor is water en glaciale erosie. Water en ijs leiden tot het kraken en verpletteren van rotsen en transporteren het gefragmenteerde materiaal naar de laaglanden. Hierdoor ontstaan geulen, canyons en bergdalen, en dus ook ribbels. Aangezien de waterlopen die het drainagesysteem van een bepaald gebied vormen van nature een dendritische structuur hebben (buiten woestijngebieden, natuurlijk), een soortgelijke opbouw komt ook voor bij de noksystemen. Maar waarom zijn de onderlinge relaties tussen het aantal ruggen met een verschillend aantal takken zo gelijk voor verschillende soorten bergen?
"De situatie wordt duidelijker als we naast water ook zwaartekracht beschouwen, " legt Dr. Kwapien uit. "Wanneer steenmateriaal wordt verpletterd, het wordt onderworpen aan de dynamiek van losse lichamen, ongeacht de chemische samenstelling. Losse lichamen op hellingen kunnen daar alleen blijven als de hellingshoeken niet te groot zijn. De hellingen mogen niet te steil zijn. Daarom wordt de diepte van dalen in de natuur beperkt door hun eigen breedte. Smalle rivierkloven met bijna verticale wanden bestaan pas in een vroeg stadium van beeldvorming. Ze zijn zeldzaam in volwassen bergformaties omdat hun muren al schuin zijn gelopen."
Het bestaan van riviersystemen die water uit een bepaald gebied afvoeren, erosie verpletterende rotsen en snijdende valleien, evenals zwaartekracht aardverschuivingen van rotspuin betekenen dat de ruggen niet willekeurig dicht bij of ver van elkaar kunnen zijn. Er is een optimale regeling, onafhankelijk van de eigenschappen van de bergketen en geven de bergen een aantal universele kenmerken.
De bovenstaande waarnemingen worden aangevuld met een andere waarneming van de IFJ PAN-fysici, met betrekking tot de afmetingen van de fractale nokstructuren. De fractale dimensie beschrijft hoe ruw de structuur van het object is. De lijn van een enkele richel heeft een afmeting van 1. Als de lijnen (ribbels) extreem dicht zijn geplaatst, hun fractale dimensie zou overeenkomen met de dimensie van het oppervlak, en zou daarom gelijk zijn aan 2. De onderzoekers toonden aan dat als de nokstructuren worden weergegeven als grafieken waarvan de knooppunten de snijpunten van de richels zijn (het is in deze snijpunten dat pieken het meest voorkomen), en de randen van de grafieken zijn de richels die de pieken verbinden, dan zouden de fractale afmetingen van zulke grafieken met een goede benadering gelijk zijn aan het getal... 5/3.
"In sommige grafieken zien we de hiërarchie van bergstructuren, in andere hun fractaliteit. In beide gevallen, voor alle soorten bergen komen we dezelfde waarden van de juiste getallen tegen. Dit universalisme geeft stof tot nadenken, " stelt prof. Stanislaw Drozdz (IFJ PAN, Technische Universiteit van Krakau).
Als verschillende bergketens qua grootte zo op elkaar lijken, waar zijn de bronnen van diversiteit in de bergen? Zal het mogelijk zijn om ze te bestuderen met behulp van grafentheorie en fractale meetkunde? Zal het mogelijk zijn om een model te maken waarin een evoluerende grafiek de opeenvolgende stadia van de vorming van een bergsculptuur nabootst? Eindelijk, zal het mogelijk zijn om de transformatie van nokkaarten in grafieken in de praktijk toe te passen, bijvoorbeeld in cartografie? Deze vragen - en vele andere - zullen alleen worden beantwoord door toekomstig onderzoek.
 Twee bacteriële co-culturen verbeteren de microbe-co-afbraak van dicarboximide-fungiciden
Twee bacteriële co-culturen verbeteren de microbe-co-afbraak van dicarboximide-fungiciden Nieuwe inzichten in de vorming van metalen bulkglazen
Nieuwe inzichten in de vorming van metalen bulkglazen Zwitsers zakmeskatalysator kan aardgas schoner maken
Zwitsers zakmeskatalysator kan aardgas schoner maken Welke plaats in de wereld krijgt de meeste zure regen?
Welke plaats in de wereld krijgt de meeste zure regen?  Wetenschappers zorgen voor doorbraak vitamine B12
Wetenschappers zorgen voor doorbraak vitamine B12
 Nieuwe stofbronnen van een krimpende Salton Sea hebben negatieve ecologische en gezondheidseffecten
Nieuwe stofbronnen van een krimpende Salton Sea hebben negatieve ecologische en gezondheidseffecten Dubbele aanpak nodig om zinkende steden en verblekende koralen te redden
Dubbele aanpak nodig om zinkende steden en verblekende koralen te redden Zwervende bandieten en geplunderde kustlijnen:hoe de wereldwijde honger naar zand een crisis aanwakkert
Zwervende bandieten en geplunderde kustlijnen:hoe de wereldwijde honger naar zand een crisis aanwakkert Oceaan circulatie, in combinatie met veranderingen in de passaatwind, beperkt efficiënt de verschuiving van tropische regenvalpatronen
Oceaan circulatie, in combinatie met veranderingen in de passaatwind, beperkt efficiënt de verschuiving van tropische regenvalpatronen Nieuwe studie analyseert vulkanische dodelijke slachtoffers in meer detail dan ooit tevoren
Nieuwe studie analyseert vulkanische dodelijke slachtoffers in meer detail dan ooit tevoren
Hoofdlijnen
- De ongelooflijke reis van de eerste Afrikaanse schildpad die in Europa aankwam
- Hebben alle mensen een uniek genotype en fenotype?
- De reden voor incubatie bij verschillende temperaturen in de microbiologie
- Tumorsuppressorgenen: wat is het?
- Nieuwe online database brengt het genoom in beeld met behulp van moleculaire structuur
- Fun Biology Presentatie Onderwerpen
- Hoe maak je een celmodel van een Amoeba
- Het voordeel testen van linkshandig zijn in de sport
- Een botanisch mysterie opgelost door fylogenetische tests
- Thuiswerken maakt ons productiever en innovatiever, zegt enquête

- Hybride werken:hoe maak je er een succes van

- Vrouwen met een verstandelijke of cognitieve beperking lopen extra online risico's

- Grote oude loopvogels uit Australië, Europa en Noord-Amerika bleken verwant te zijn

- STEM:Pogingen om meer kinderen te inspireren, zouden onderwijsongelijkheden kunnen verankeren

 Juno-ruimtevaartuig vliegt 10 juli over Jupiters Grote Rode Vlek
Juno-ruimtevaartuig vliegt 10 juli over Jupiters Grote Rode Vlek Spin-golfcircuits op nanoschaal gebaseerd op geconstrueerde herconfigureerbare spin-texturen
Spin-golfcircuits op nanoschaal gebaseerd op geconstrueerde herconfigureerbare spin-texturen Rent-a-captain:Zuid-Afrika vult wereldwijd tekort aan piloten aan
Rent-a-captain:Zuid-Afrika vult wereldwijd tekort aan piloten aan Foo Fighters
Foo Fighters  Zijn oorlogen de drijvende kracht achter technologische vooruitgang?
Zijn oorlogen de drijvende kracht achter technologische vooruitgang?  Het richten op een enkel eiwit kan een breed scala aan virussen behandelen
Het richten op een enkel eiwit kan een breed scala aan virussen behandelen Wat zijn de oorzaken van waterstress?
Wat zijn de oorzaken van waterstress?  winden, regent het westen van India terwijl de cycloon wegdraait
winden, regent het westen van India terwijl de cycloon wegdraait
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

