
Wetenschap
Wiskundigen stellen eerste continu zelfgeorganiseerd kriticiteitsmodel voor
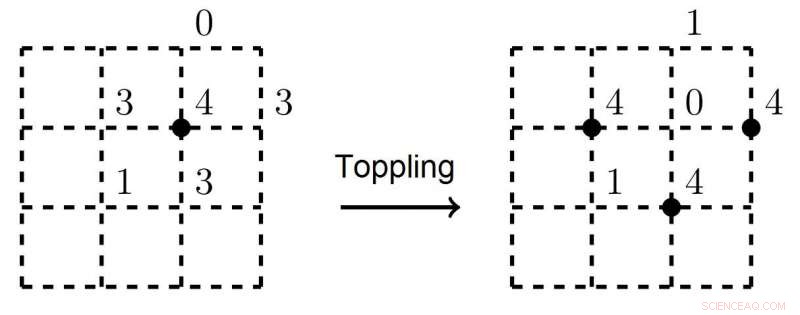
De zwarte stip op de linker figuur markeert een onstabiel hoekpunt. Na een lawine, drie aangrenzende hoekpunten worden onstabiel en zullen instorten Krediet:Nikita Kalinin, Hogere School of Economics - Sint-Petersburg
Een internationale groep onderzoekers (de eerste auteur is Nikita Kalinin, Hogere Economische School — Sint-Petersburg, de laatste auteur is Ernesto Lupercio, CINVESTAV, Mexico) heeft het eerste continue model gepresenteerd dat zelfgeorganiseerde kriticiteit beschrijft. De voorgestelde oplossing is eenvoudiger en universeler dan het klassieke zandstapelmodel. Het integreert gebieden die zo ver van elkaar verwijderd zijn als economie, ontwikkelingsbiologie, en zwaartekracht in de context van tropische geometrie. De krant is gepubliceerd in Proceedings van de National Academy of Sciences .
Een systeem is in een kritieke toestand als een externe kracht, hoe klein ook, kan een lawine-effect veroorzaken, waardoor het gedrag van het systeem verandert. Deze omvatten faseovergangen:zodra een enkel ijskristal tevoorschijn komt in water dat is afgekoeld tot nul graden Celsius, een ijscluster zal zich onmiddellijk beginnen te vormen.
Er zijn bepaalde dynamische systemen die neigen naar een kritieke toestand - aardbevingen zijn een illustratief voorbeeld. Hoewel een bepaalde temperatuur en druk nodig zijn om water te laten bevriezen, er hoeven geen precieze parameters te worden vervuld om een aardbeving te laten plaatsvinden. De belangrijkste oorzaak van aardbevingen is de continue beweging van tektonische platen, en het voorspellen van het exacte moment waarop het systeem een kritieke toestand bereikt en een lawine veroorzaakt, is vrijwel onmogelijk.
Veel onderzoekers hebben geprobeerd het mysterie van aardbevingen op te lossen. In het midden van de 20e eeuw, Amerikaanse seismologen Gutenberg en Richter toonden een verband aan tussen de omvang en het totale aantal aardbevingen in een bepaalde regio. Deze relatie wordt beschreven door de machtswet uitgedrukt als een rechte lijn op een dubbele logaritmische schaal.
Fenomenen die deze eigenschap delen, zijn sindsdien gevonden in de geofysica, kosmologie, economie, risicobeheertheorie en andere gebieden. Ze kunnen allemaal worden beschreven door de theorie van zelfgeorganiseerde kriticiteit (SOC).
Het concept van SOC is geïntroduceerd door Per Bak, Chao Tang en Kurt Wiesenfeld in 1987. In hun baanbrekende artikel, ze brachten het archetypische voorbeeld van een SOC-systeem naar voren:het Sandpile-model. Stel je een vierkant raster voor met zandkorrels in elk van zijn hoekpunten, waarin met een bepaalde frequentie nieuwe korrels op het rooster vallen. Er wordt aangenomen dat als er niet meer dan drie zandkorrels in elk hoekpunt zijn, het systeem blijft stabiel. Maar zodra een vierde zandkorrel bovenop een hoekpunt valt, het valt om, en het zand glijdt langs deze piek naar beneden en wordt herverdeeld naar aangrenzende hoekpunten. Het omvallen zal in een lawine doorgaan totdat het systeem weer in evenwicht is. De belangrijkste ontdekking van de natuurkundigen was dat het aantal hoekpunten dat omvalt (d.w.z. de grootte van het ingestorte gebied) voldoet aan een machtswetverdeling.
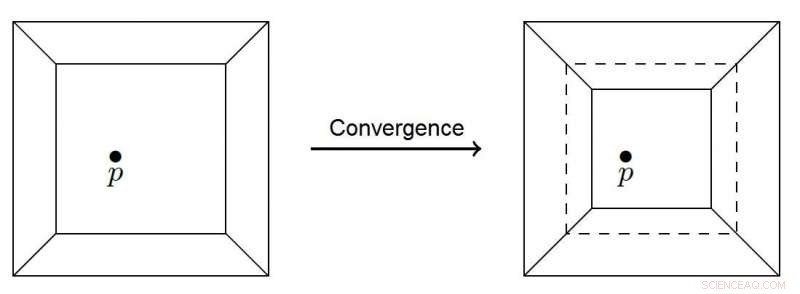
Veelhoek convergerend naar een punt. Krediet:Nikita Kalinin, Hogere School of Economics - Sint-Petersburg
Het zandstapelmodel is lange tijd het klassieke model geweest dat SOC beschrijft. Echter, het beschrijft de dynamiek van kritieke systemen alleen op fenomenologisch niveau en kan niet worden gebruikt om een aardbeving te simuleren of het gedrag van een echte zandhoop te voorspellen.
"Het oude zandstapelmodel, puur combinatorisch zijn, staat enigszins los van de grote wereld van de wiskunde. Ons model is een stap vooruit, omdat het alle voordelen van het zandstapelmodel heeft, maar het is ook geometrisch en continu, waardoor het veel gemakkelijker te gebruiken is, " legt auteur Nikita Kalinin uit, senior research fellow van het HSE International Laboratory of Game Theory and Decision Making. "We hebben aangetoond dat correlaties van machtswetten kunnen worden verkregen in een continu systeem dat geen cellulaire automaat is met behulp van tropische geometrie, die tegenwoordig veel toepassingen heeft."
"Tropische meetkunde is een eenentwintigste-eeuwse tak van meetkunde, geïnspireerd op de klassieke algebraïsche meetkunde die tot bloei is gekomen vanwege zijn connecties met vele wetenschapsgebieden, voornamelijk snaartheorie, " zegt Dr. Ernesto Lupercio van de CINVESTAV.
In plaats van het raster dat wordt gebruikt in het klassieke zandstapelmodel, het nieuwe tropische zandstapelmodel beschouwt een tropische curve - een vlakke grafiek met rechtlijnige randen - ingesloten in een vierkant. De curve verdeelt het vierkant in veelhoekige gebieden, elk met een willekeurig gekozen reeks punten. Wanneer een nieuw punt wordt toegevoegd, de tropische curve probeert er doorheen te gaan, en het veelhoekige gebied dat het punt bevat, wordt samengetrokken via een parallelle overdracht van zijn randen. Zodra een van de randen de punt raakt, het proces stopt. Er wordt dan een nieuw punt toegevoegd, en het begint weer helemaal opnieuw. Het vorige punt kan weer afwijken van de curve, en het systeem zal ernaartoe gaan bewegen.
Dit convergentieproces is een eindige variant van het toevoegen van zandkorrels aan een zandhoop. Bij het nieuwe model de lawinegrootte komt overeen met het gebied dat door de convergerende regio's wordt geveegd in het proces dat wordt gestart door een willekeurig punt toe te voegen. De wetenschappers hopen dat hun model de relaties tussen verschillende fenomenen die SOC-eigenschappen vertonen, zal helpen verduidelijken.
"We kunnen overeenkomsten in verschillende fenomenen waarnemen door de lens van de wiskunde. Tropische meetkunde heeft toepassingen in de snaartheorie, economie en ontwikkelingsbiologie. De waarde van ons werk ligt in het vinden van verbanden op onverwachte plekken. Het betekent dat de methoden die op het ene gebied worden toegepast, op een ander gebied kunnen worden toegepast. Je hoeft alleen maar de volgende stap te zetten, ' zegt Kalinin.
 Satellieten helpen bij het onderzoeken van orkanen
Satellieten helpen bij het onderzoeken van orkanen Fotosynthese is een miljard jaar eerder ontstaan dan we dachten, studie toont
Fotosynthese is een miljard jaar eerder ontstaan dan we dachten, studie toont Waren dinosaurussen de meest succesvolle dieren op aarde?
Waren dinosaurussen de meest succesvolle dieren op aarde?  Verbeterd model schat impact van ozon op sojagewassen
Verbeterd model schat impact van ozon op sojagewassen Kleine stroompjes in agrarische ecosystemen zijn zwaar vervuild met pesticiden
Kleine stroompjes in agrarische ecosystemen zijn zwaar vervuild met pesticiden
Hoofdlijnen
- Hoe zangvogels een nieuw lied leren
- Onverwachte regulatie van transcriptiefactoren die cruciaal zijn voor ontwikkeling
- Kan boos worden goed voor je zijn?
- Losse huid en slap volume beschermen Hagfish tegen haaienbeten
- De voordelen van Stained Bacteria
- Wat doet de temporale kwab?
- Hoe maak je een Bacterial Flowchart
- Welke landen hebben de kleinste persoonlijke ruimte?
- De voor- en nadelen van het Bacillus-expressiesysteem
- Pandemie duwt sterke daling van buitenlandse studenten

- Een goede baan voor gevonden robots - omgaan met onze gênante problemen

- Wetenschappers beschrijven het meest complete fossiel uit de vroege stadia van de evolutie van de uil
- Nomaden bepaalden voedseltrends langs de zijderoutes

- De kracht van empathie bij productontwikkeling

 E-bike gemopper echo in de Beierse Alpen
E-bike gemopper echo in de Beierse Alpen Van ontziltingsafval een nuttige hulpbron maken
Van ontziltingsafval een nuttige hulpbron maken In het laboratorium gekweekt vlees zou over 3 jaar in restaurants kunnen liggen (update)
In het laboratorium gekweekt vlees zou over 3 jaar in restaurants kunnen liggen (update) Valse verhalen beweren dat NASA bekende lithium te hebben verspreid
Valse verhalen beweren dat NASA bekende lithium te hebben verspreid Klimaateffecten op gezondheid en stedelijke gebieden:hittegolven en sterftecijfer
Klimaateffecten op gezondheid en stedelijke gebieden:hittegolven en sterftecijfer Onthulling van technologieën voor toekomstige draagraketten
Onthulling van technologieën voor toekomstige draagraketten Hoe inzichten in intergenerationele overdracht de sociale mobiliteit kunnen vergroten
Hoe inzichten in intergenerationele overdracht de sociale mobiliteit kunnen vergroten Hoe een hoekfrequentie berekenen
Hoe een hoekfrequentie berekenen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

