Op 5 januari, Rosa Winter promoveert in rekenkundige meetkunde. Ze deed onderzoek naar oplossingen van vergelijkingen die zogenaamde 'del Pezzo-oppervlakken' definiëren." "Ik hou van geometrie omdat ik me de vormen en objecten kan voorstellen en tekenen, ", zegt Winter. "Dat maakt abstracte wiskunde tastbaarder."

In wiskunde, het is soms handig om abstracte vergelijkingen te bestuderen met behulp van geometrische objecten, zoals cirkels, bollen, octaëders, of zelfs hoger-dimensionale objecten. Het veld dat meetkunde verbindt met abstracte vergelijkingen wordt rekenkundige meetkunde genoemd. doctoraat kandidaat Rosa Winter paste dit specifieke type geometrie toe in haar proefschrift.

Oppervlakken tekenen

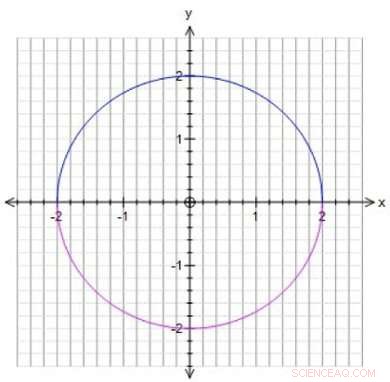
Wiskundige vergelijkingen kunnen geometrische objecten definiëren, wat betekent dat het mogelijk is om oplossingen voor die vergelijkingen te bestuderen met behulp van geometrie. Bijvoorbeeld, als je wilt weten welke getallen je kunt invoeren om x^2+y^2 gelijk te maken aan 4, je kunt alle punten (oplossingen) tekenen waarvoor x^2+y^2=4. Dit resulteert in een cirkel met straal 2, welke shows, bijvoorbeeld, dat het punt x=2, y=0 is een oplossing. U kunt ook zoeken naar specifieke oplossingen, zoals punten op de cirkel waar x en y breuken zijn (1/3e, 1/5e, maar ook, 0, 2, enzovoort.). Die fractionele oplossingen worden rationale punten genoemd. Winter bestudeerde rationale punten op oppervlakken. "Oppervlakken zijn altijd tweedimensionaal, zelfs als ze in acht dimensies leven, " zegt Winter. "Wat betekent dat ik vlakken kan tekenen, het maken van de abstracte wiskunde meer intuïtief voor mij."

Vraag van een miljoen dollar

Het vinden van rationele punten op geometrische objecten is zelden eenvoudig. Dit wordt getoond, bijvoorbeeld, door het zogenaamde "Birch en Swinnerton-Dyer vermoeden." Dit nog onbewezen wiskundige vermoeden maakt deel uit van de Millennium Prize Problems. Het Clay Mathematics Institute kent een miljoen dollar toe aan een correcte oplossing voor elk van deze problemen. Het vermoeden gaat over rationale punten op elliptische krommen. Zoals cirkels, elliptische krommen zijn geometrische objecten gedefinieerd door bepaalde vergelijkingen. Als je ze tekent, ze zien eruit als gebogen lijnen. Winter:"Zelfs op elliptische bochten, waar we redelijk wat van weten, het is niet gemakkelijk om de reeks rationale punten te bepalen."

Del Pezzo-oppervlakken

Helaas, Winter heeft het miljoen dollar niet opgehaald tijdens haar Ph.D. Onderzoek. Ze werkte niet aan rationale punten op elliptische krommen, maar op zogenaamde 'del Pezzo-oppervlakken van graad 1'." Winter:"Vanuit geometrisch oogpunt dit zijn niet de moeilijkste, meest gecompliceerde oppervlakken, maar ze bevatten nog steeds onbeantwoorde wiskundige vragen." Ze toonde voor een deel van deze familie van oppervlakken dat het een oneindig aantal rationale punten bevat die niet clusteren; ze kunnen verspreid over de oppervlakken worden gevonden. Als rationale punten zichtbaar waren als rode stippen en je zou over zo'n del-Pezzo-oppervlak kunnen lopen, je zou overal rode rationele punten zien.

Sinds september, Winter heeft als postdoc gewerkt bij het Max Planck Institute for Mathematics in the Sciences in Leipzig. Hier leert ze onder andere, hoe meetkunde en abstracte wiskunde toe te passen in andere wetenschappen, zoals biologie en natuurkunde.