
Wetenschap
Wiskundigen ontrafelen draad van snaartheorie

Voorbeeld van een doorsnede van K3-oppervlak in 3-ruimte, vergelijkbaar met een model Utah State University en University of Missouri-St. Louis-wiskundigen onderzochten snaardualiteiten tussen F-theorie en heterotische theorie in acht dimensies. Krediet:USU
Simpel gezegd, snaartheorie is een voorgestelde methode om alles uit te leggen. Werkelijk, er is niets simpels aan. Snaartheorie is een theoretisch raamwerk uit de natuurkunde dat eendimensionale, trillende vezelachtige objecten genaamd "snaren, " die zich door de ruimte voortplanten en met elkaar interageren. Stuk voor stuk, energetische geesten ontdekken en ontcijferen fundamentele snaren van het fysieke universum met behulp van wiskundige modellen. Onder deze onverschrokken ontdekkingsreizigers bevinden zich de wiskundigen van de Utah State University, Thomas Hill en zijn faculteitsmentor, Andreas Malmendier.
Met collega Adrian Clingher van de Universiteit van Missouri-St. Lodewijk, het team publiceerde bevindingen over twee takken van de snaartheorie in de krant, "De dualiteit tussen F-theorie en de heterotische snaar in D =8 met twee Wilson-lijnen, " op 7 augustus 2020 online editie van Letters in Mathematical Physics. Het werk van de USU-onderzoekers wordt ondersteund door een subsidie van de Simons Foundation.
"We hebben een speciale familie van K3-oppervlakken bestudeerd:compacte, verbonden complexe oppervlakken van dimensie 2 - die belangrijke geometrische hulpmiddelen zijn voor het begrijpen van symmetrieën van fysieke theorieën, " zegt Heuvel, die in 2018 afstudeerde aan het honoursprogramma van de USU met een bachelor wiskunde en afgelopen voorjaar een master wiskunde heeft afgerond. "In dit geval, we onderzochten een snaardualiteit tussen F-theorie en heterotische snaartheorie in acht dimensies."
Hill zegt dat het team heeft bewezen dat de K3-oppervlakken die ze hebben onderzocht, vier unieke manieren toelaten om de oppervlakken te snijden als Jacobiaanse elliptische vezels, vorming van torusvormige vezels. De onderzoekers construeerden expliciete vergelijkingen voor elk van deze vezels.
"Een belangrijk onderdeel van dit onderzoek is het identificeren van bepaalde geometrische bouwstenen, genaamd 'delers, " binnen elk K3-oppervlak, "zegt hij. "Met behulp van deze delers, cruciale geometrische informatie wordt vervolgens gecodeerd in een abstracte grafiek."
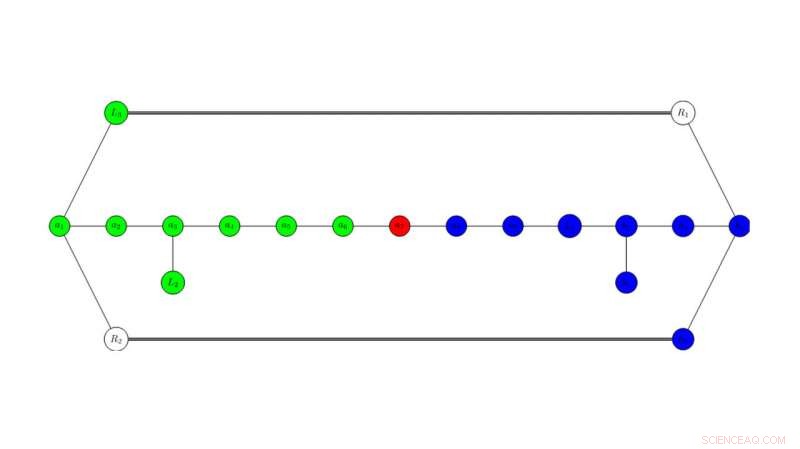
Met behulp van een abstracte grafiek, Onderzoekers van de Utah State University identificeren delers binnen elk K3-oppervlak om verschillende symmetrieën te onderzoeken. De verschillende Jacobiaanse elliptische fibraties komen overeen met specifieke kleuren van een verbonden subset van de knooppunten van de grafiek. De symmetrieën van de grafiek en de mogelijke kleuringen van de knopen zijn cruciaal voor het begrijpen van de symmetrieën van de onderliggende fysische theorieën. Krediet:Malmendier/Hill, USU
Dit proces, heuvel zegt, stelt onderzoekers in staat om symmetrieën van onderliggende fysieke theorieën te onderzoeken die door de grafiek worden aangetoond.
"Je kunt deze familie van oppervlakken zien als een brood en elke vezel als een 'plakje' van dat brood, " zegt Malmendier, universitair hoofddocent bij de afdeling Wiskunde en Statistiek van de USU. "Door de opeenvolging van plakjes te onderzoeken, we kunnen visualiseren, en beter begrijpen, het hele brood."
De onderneming die in de krant wordt beschreven, hij zegt, staat voor uren van nauwgezet "papier en potlood" werk om de stellingen van elk van de vier vezels te bewijzen, gevolgd door elke stelling door moeilijke algebraïsche formules te duwen.
"Voor het laatste deel van dit proces, we gebruikten Maple Software en het gespecialiseerde Differential Geometry Package ontwikkeld bij USU, die onze computationele inspanningen stroomlijnden, ' zegt Malmendier.
 Hoe groot is een fragment?
Hoe groot is een fragment? Scanner voor schilderijen blijkt veelbelovende nieuwe CSI-tool
Scanner voor schilderijen blijkt veelbelovende nieuwe CSI-tool Op pijnboomsap gebaseerd plastic:een potentiële gamechanger voor de toekomst van duurzame materialen
Op pijnboomsap gebaseerd plastic:een potentiële gamechanger voor de toekomst van duurzame materialen Mogelijke nieuwe antivirale middelen tegen COVID-19, herpes
Mogelijke nieuwe antivirale middelen tegen COVID-19, herpes Nieuwe technologie om bittere amandelen in realtime te detecteren
Nieuwe technologie om bittere amandelen in realtime te detecteren
 Europese wetenschappers, Ambtenaren waarschuwen tegen Amerikaans klimaatplan
Europese wetenschappers, Ambtenaren waarschuwen tegen Amerikaans klimaatplan Uit onderzoek blijkt dat biologisch afbreekbare alternatieven niet beter zijn voor het milieu
Uit onderzoek blijkt dat biologisch afbreekbare alternatieven niet beter zijn voor het milieu Welk deel van de plant maakt zaden?
Welk deel van de plant maakt zaden?  Hoe beter ondergedoken vegetatie zich ontwikkelt, de grotere stikstofverwijdering vindt plaats in meersedimenten
Hoe beter ondergedoken vegetatie zich ontwikkelt, de grotere stikstofverwijdering vindt plaats in meersedimenten Extreem gevaarlijke orkaan Eta treft Nicaragua
Extreem gevaarlijke orkaan Eta treft Nicaragua
Hoofdlijnen
- Kevers felle kleuren gebruikt voor camouflage in plaats van roofdieren te waarschuwen
- Waarom zijn mensen hun staart kwijtgeraakt?
- Genetische barcodes worden gebruikt om cruciale populaties in een ecosysteem van koraalriffen te kwantificeren
- Deze dans wordt uitgevoerd:honderden mannelijke kikkersoorten veranderen van kleur rond de paringstijd
- Gebruik van microscopen in de wetenschap
- mensen, in tegenstelling tot apen, verander de concurrentiesituatie in een coöperatieve
- Voeding die de productiviteit in de intensieve veehouderij verhoogt
- Cambodja neemt lading ivoor in beslag, verborgen in holle boomstammen
- Hoe virussen de manier veranderen waarop we naar evolutie kijken
 Hoe microgrammen om te zetten in micromoles
Hoe microgrammen om te zetten in micromoles Nieuwe detectiemethode verandert siliciumcamera's in midden-infrarooddetectoren
Nieuwe detectiemethode verandert siliciumcamera's in midden-infrarooddetectoren Onderzoekers vinden lekkende apps die de privacy in gevaar brengen
Onderzoekers vinden lekkende apps die de privacy in gevaar brengen Wat als er geen Google was?
Wat als er geen Google was?  Wat geven de kleuren aan op een pH-teststrookpapier?
Wat geven de kleuren aan op een pH-teststrookpapier?  Nieuwe microfluïdische benadering voor de gerichte assemblage van functionele materialen
Nieuwe microfluïdische benadering voor de gerichte assemblage van functionele materialen De impact van massatoerisme van walvishaaien op de koraalriffen in de Filippijnen
De impact van massatoerisme van walvishaaien op de koraalriffen in de Filippijnen Nieuwe manier om staal te maken dat zowel sterker als taaier is
Nieuwe manier om staal te maken dat zowel sterker als taaier is
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com






