
Wetenschap
Onderzoekers vinden verband tussen snaartheorie in een klasse van complexe getallen
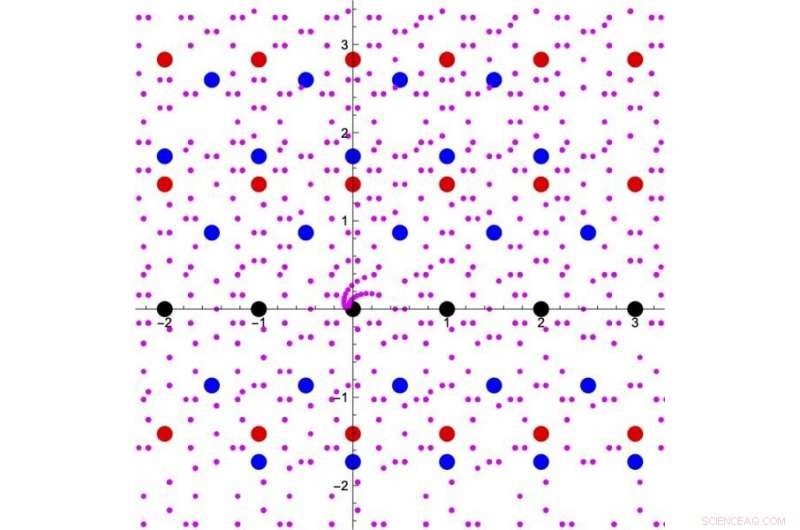
Figuur 1. Uitbreiding van het begrip integrale "getallen". Zwarte punten zijn de gewone gehele getallen die in een complex vlak worden weergegeven. Optellen of vermenigvuldigen van een paar zwarte punten resulteert in een ander zwart punt. Alle rode punten en blauwe punten in deze figuur zijn oplossingen van enkele kwadratische vergelijkingen met gehele coëfficiënten. De paarse punten zijn oplossingen van een aantal quartic vergelijkingen met gehele coëfficiënten. Dus, we kunnen die punten ook zien als een onderdeel van "getallen". Optellen en vermenigvuldigen tussen zwart-of-rode punten blijven binnen de "getallen" weergegeven in zwart-of-rode punten, en evenzo, die bewerkingen van zwart-rood-blauw-of-paarse punten blijven binnen de "getallen" in zwart-rood-blauw-of-paarse punten. Op deze manier, het is mogelijk om de verzameling integrale "getallen" geleidelijk uit te breiden. Krediet:Kavli IPMU
Een samenwerking van een wiskundige en een natuurkundige heeft aangetoond dat de modulaire vormen die worden geassocieerd met elliptische krommen met complexe vermenigvuldigingen worden uitgedrukt in termen van waarneembare objecten in de supersnaartheorie.
Het concept van getallen kan worden uitgebreid van gehele getallen en rationale getallen tot alle reële getallen en complexe getallen, alles in een keer. Maar het is ook mogelijk om het concept geleidelijk uit te breiden, door de wortels van veeltermen met rationale getalcoëfficiënten (zoals de vierkantswortel van 2 en de vierkantswortel van 3) beetje bij beetje op te tellen (Figuur 1). Deze speciale klasse van complexe getallen wordt 'getallen' genoemd. De precieze details van hoe het begrip getallen kan worden uitgebreid, wordt beschouwd als een van de belangrijke thema's in de getaltheorie.
Sinds enkele decennia is onderzoekers hebben geprobeerd dit probleem aan te pakken en te begrijpen. Men zou een geometrisch object kunnen specificeren door vergelijkingen met eerst de "getallen", en beschouw dan de verzameling punten in het geometrische object waarvan de waarden de 'getallen' zijn. Naarmate het begrip getallen geleidelijk wordt uitgebreid, en de reeks "getallen" uitgebreid, steeds meer punten in het geometrische object worden geteld (Figuur 2). Het idee is dat de manier waarop het aantal punten in het geometrische object toeneemt, licht zal werpen op hoe de reeks "getallen" uitbreidt. Verder, deze informatie over de groeisnelheid van het aantal punten in het geometrische object is verpakt in een functie die de inverse Mellin-transformatie van de L-functie wordt genoemd, dat is een functie die de informatie bevat over hoe snel het aantal punten in een meetkundig object groeit naarmate het concept van getallen wordt uitgebreid. Deze functie is naar verwachting een modulaire vorm, een functie die onder bepaalde bewerkingen invariant blijft. Dit vermoeden staat bekend als het vermoeden van Langlands.
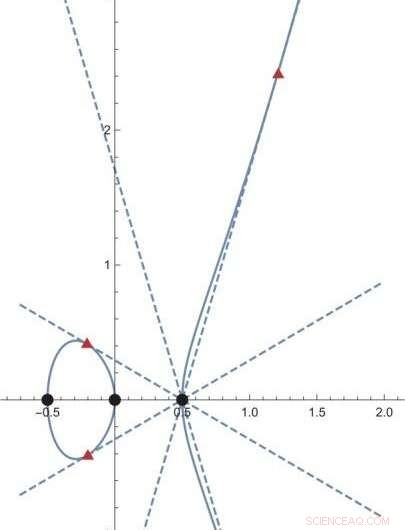
Figuur 2. Een geometrisch object gegeven door y^2 =4 x^3 - x wordt weergegeven door een dunne blauwe curve. In dit voorwerp, de drie zwarte punten hebben hun waarden in de gewone gehele getallen. Anderzijds, de drie punten in rode driehoeken hebben hun waarden in een meer uitgebreide reeks "getallen" (de x-coördinaten hebben de vorm (p+q sqrt{2}) met rationale getallen p en q; de y-coördinaten zijn ingewikkelder) . Naarmate het begrip "getallen" wordt uitgebreid, het aantal punten met hun waarden in de "getallen" neemt toe, zelfs voor een bepaald geometrisch object. Krediet:Kavli IPMU
Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU) Universitair hoofddocent en deeltjestheoreticus Taizan Watari en onderzoeker rekenkundige meetkunde aan de Middle East Technical University Northern Cyprus Campus en Kavli IPMU Visiting Scientist Satoshi Kondo durfde zich af te vragen waarom dergelijke functies onder bepaalde omstandigheden onveranderlijk zijn activiteiten.
In de snaartheorie het is bekend dat een klasse van waarneembare waarden (a) invariant zijn onder de operaties (x) waarnaar al is verwezen. De invariantie onder de operaties is een onmisbare eigenschap in de theoretische constructie van de supersnaartheorie. Dus, de onderzoekers toonden aan dat de inverse Mellin-transformaties van de L-functies van geometrische objecten (b) worden uitgedrukt in termen van de bovenstaande klasse van waarneembare objecten (a) in superstringtheorie met die geometrische objecten ingesteld als de doelruimten. Als resultaat, hieruit volgt dat de functies die de informatie bevatten over hoe het concept van getallen wordt uitgebreid, de inverse Mellin transformeert, (b) onder bepaalde operaties invariant moet zijn, die modulaire vormen moeten zijn, (x) om redenen vanuit het perspectief van de supersnaartheorie.
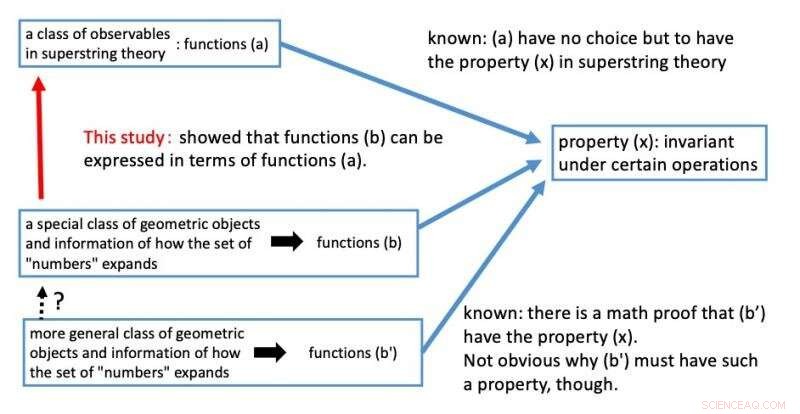
Figuur 3. Samenvatting van dit onderzoek. Krediet:Kavli IPMU
Opgemerkt moet worden dat het bovenstaande resultaat alleen wordt verkregen voor de klasse van geometrische objecten die elliptische krommen met complexe vermenigvuldigingen worden genoemd. De vraag blijft open of de functies voor een meer algemene klasse van meetkundige objecten (b) worden uitgedrukt in termen van waarneembare objecten in de supersnaartheorie (a).
Details van deze studie werden gepubliceerd op 22 februari, 2019, in Communicatie in wiskundige natuurkunde .
 Coin Corrosion Science Experiments voor kinderen
Coin Corrosion Science Experiments voor kinderen  Wat zijn de componenten van de atoomstructuur?
Wat zijn de componenten van de atoomstructuur?  Hoe klimaatveranderende koolstofdioxide om te zetten in plastic en andere producten?
Hoe klimaatveranderende koolstofdioxide om te zetten in plastic en andere producten? Onderzoekers rapporteren betere manier om organische bio-elektronica te maken
Onderzoekers rapporteren betere manier om organische bio-elektronica te maken Recombinant collageenpolypeptide als een veelzijdig biomateriaal voor bottransplantaten
Recombinant collageenpolypeptide als een veelzijdig biomateriaal voor bottransplantaten
 De ontbrekende schakel tussen exploderende sterren, wolken, en klimaat op aarde
De ontbrekende schakel tussen exploderende sterren, wolken, en klimaat op aarde Nieuwe publicatie onderzoekt gevolgen van grondwateruitputting voor de landbouw
Nieuwe publicatie onderzoekt gevolgen van grondwateruitputting voor de landbouw Krachtige aardbeving in Filipijnen:1 doodt beschadigt huizen, wegen
Krachtige aardbeving in Filipijnen:1 doodt beschadigt huizen, wegen Drie keer grotere reducties in de uitstoot van broeikasgassen in de VS dan eerder gemeld
Drie keer grotere reducties in de uitstoot van broeikasgassen in de VS dan eerder gemeld Euraziatische anomalieën in de atmosferische circulatie kunnen van de winter tot de volgende lente aanhouden
Euraziatische anomalieën in de atmosferische circulatie kunnen van de winter tot de volgende lente aanhouden
Hoofdlijnen
- The Differences Between Kinetochore & Nonkinetochore
- Hoe handhaaft het plasmamembraan homeostase?
- Wetenschappers beginnen gedurfde pogingen tot instandhouding om de vaquita-bruinvis van uitsterven te redden
- Genetische ontdekking nog een hulpmiddel in de strijd tegen tarweplagen
- Studie vindt toename van herbicide bij oudere volwassenen
- De controverse over het menselijk brein Nieuwe cellen maken
- DNA-bewijs zet neushoornstropers achter tralies, studie toont
- Wat is het verschil tussen ras en etniciteit?
- Wat zijn de functies van co-enzymen?
 Milieugroenheid kan de testscores van studenten niet verbeteren, studie vondsten
Milieugroenheid kan de testscores van studenten niet verbeteren, studie vondsten Een konijn ontleden
Een konijn ontleden  Waarom is de JWST infrarood?
Waarom is de JWST infrarood?  Nieuwe tool gebruikt AI om nepnieuws te markeren voor media-factcheckers
Nieuwe tool gebruikt AI om nepnieuws te markeren voor media-factcheckers Op weg naar een slimme pleister die automatisch insuline toedient wanneer dat nodig is
Op weg naar een slimme pleister die automatisch insuline toedient wanneer dat nodig is Hoe het klimaat de levering van zonne- en windenergie beïnvloedt
Hoe het klimaat de levering van zonne- en windenergie beïnvloedt Multimodale beeldvorming toont aan dat spanning de chemie in een fotovoltaïsch materiaal kan stimuleren
Multimodale beeldvorming toont aan dat spanning de chemie in een fotovoltaïsch materiaal kan stimuleren China, Economische ontwikkeling in India sleutel tot het bereiken van de millenniumdoelstelling voor veilig drinkwater
China, Economische ontwikkeling in India sleutel tot het bereiken van de millenniumdoelstelling voor veilig drinkwater
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com






