Fijne 29 februari! Het komt niet vaak voor, dus zorg dat je ervan geniet.

Maar waarom hebben we deze extra dagen? We zullen, als we dat niet deden, de seizoenen zouden geleidelijk over de kalender bewegen. In plaats van dat de midzomer op het zuidelijk halfrond rond 21 december valt, het zou in januari aankomen, dan februari, enzovoort. Na een paar eeuwen, de Australische zomer zou in juli eindigen!

Maar wat is een jaar precies? Het eenvoudigste antwoord is de hoeveelheid tijd die de aarde nodig heeft om om de zon te draaien. Op school, we leren allemaal dat dat 365 dagen is. Lekker simpel, Rechtsaf?

Er is alleen een probleem:er zijn verschillende definities van een jaar.

Het siderische jaar

Het "siderische jaar" is de klassieke definitie van een klaslokaal. Het is de tijd die de aarde nodig heeft om één ronde van de zon af te leggen en terug te keren naar precies dezelfde plaats in zijn baan, beoordeeld aan de hand van de positie van de zon ten opzichte van de achtergrondsterren.

Maar een sterrenjaar duurt geen 365 dagen. Liever, het duurt 365,256 dagen.

Dan is er nog een probleem. Naast het draaien om zijn as (die ons dag en nacht geeft), ook onze planeet wiebelt. nauwkeuriger, aardas "preces, " eens in de 26 ronddraaien, 000 jaar of zo, als een wiebelende tol.

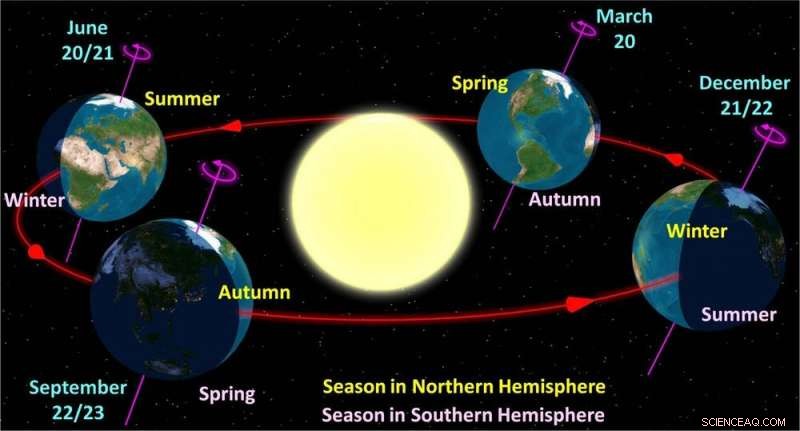
Dit is belangrijk omdat de richting waarin de as van de aarde wijst de seizoenen bepaalt. Als het zuidelijk halfrond van de zon af wijst, we ervaren onze zuidelijke winter terwijl het noordelijk halfrond de zomer ziet, en dan omgekeerd.

Maar de precessie (wiebelen) van de aardas betekent dat in 13, 000 jaar tijd, de richtingen zouden het tegenovergestelde zijn van vandaag. Vandaag, de zuidpool staat tijdens de zuidelijke midzomer naar de zon gericht, maar in 13, 000 jaar zou zijn weggekanteld (midwinter) op dezelfde plaats in de baan van de aarde.

Dit betekent dat, gedurende duizenden jaren, de locatie waarop we midwinter of midzomer in de baan van de aarde zouden ervaren, zou veranderen. Met andere woorden, als we onze kalender aan het sterrenjaar zouden koppelen, de seizoenen zouden nog steeds door de kalender verschuiven!

Het tropische jaar

Gelukkig, we hebben een andere manier om een ​​jaar te definiëren waarmee dit probleem kan worden opgelost. In plaats van de exacte tijd te meten die nodig is om om de zon te draaien, we kunnen in plaats daarvan de tijd meten tussen de lente-equinox van het ene jaar en het volgende.

De lente-equinox is het punt in de baan van de aarde waar de zon van het zuidelijk halfrond van onze hemel naar het noordelijk halfrond beweegt. Elk jaar valt het op of rond 21 maart.

De tijd tussen de ene equinox en de volgende wordt het "tropische jaar, " en is iets korter dan het sterrenjaar. Het komt op 365,24219 dagen.

Dit verschil is vrij klein (ongeveer 20 minuten), maar het komt overeen met de hoeveelheid die de aardas in die tijd heeft afgelegd - iets minder dan 1/26, 000 van een volledige ronde.

Een sprong in de toekomst

Maar wat heeft dit alles te maken met schrikkeljaren? We zullen, omdat het tropische jaar niet precies 365 dagen duurt, de datum van de lente-equinox (en midzomer, midwinter, en elk ander seizoensevenement dat u maar wilt noemen) zal geleidelijk door de kalender drijven. Als elk jaar 365 dagen had, die gebeurtenissen zouden geleidelijk later en later op de kalender vallen - met 0,24219 dagen per jaar.

Dat klinkt niet als veel, maar het zou stijgen. Na 100 jaar, de data van die gebeurtenissen zouden 24 dagen later zijn. De kalender zou uit de pas lopen met de seizoenen.

Om dit te verhelpen, we hebben schrikkeljaren, waarin we een enkele dag toevoegen aan de lengte van het jaar. Als we een enkele periode van vier jaar nemen, en bereken de gemiddelde lengte van het jaar, we krijgen 365,25 dagen, wat vrij dicht bij het echte werk ligt. Maar het is nog niet dichtbij genoeg.

De Juliaanse kalender

Deze benadering werkte lange tijd goed genoeg. In 45 voor Christus, de voorloper van de moderne kalender begon. Bekend als de Juliaanse kalender, het werd geïntroduceerd door Julius Caesar.

De Juliaanse kalender implementeerde een proces van schrikkeljaren:om de vier jaar, zonder falen, eind februari zou er een extra dag zijn.

Er waren wat problemen bij het implementeren van deze nieuwe kalender - en gedurende een paar decennia, schrikkeljaren werden om de drie jaar ten onrechte opgeteld. Dingen waren opgelost door 12AD, en vanaf dat moment elk vierde jaar had een schrikkeljaar.

Maar tegen het midden van de jaren 1500, fouten begonnen opnieuw op te stapelen. Onthoud dat deze benadering een gemiddelde jaarlengte van 365,25 dagen geeft, terwijl het echte tropische jaar 365,24219 dagen is.

Na anderhalf millennia, dit kleine verschil had ertoe geleid dat de data voor de zonnewendes met tien dagen door de kalender waren verschoven.

De Gregoriaanse kalender

Om deze zeer langzame drift op te lossen, in de tweede helft van de 16e eeuw werd een nieuwe kalender bedacht. Vernoemd naar paus Gregorius XIII, de Gregoriaanse kalender werd uitgebracht in 1582.

Het verschoof de data van het jaar, het verplaatsen van de zonnewendes terug naar hun beoogde plaats. Het paste vervolgens de manier aan waarop met schrikkeljaren werd omgegaan, om ervoor te zorgen dat die datums in de toekomst niet opnieuw verschuiven.

De kleine verandering was dat schrikkeljaren die "eeuwjaren" waren (jaren eindigend op 00) deelbaar moesten zijn door zowel 100 als 400. Als het jaar kan worden gedeeld door 100, maar niet tegen 400, het is geen schrikkeljaar.

Laten we als voorbeeld de eeuwjaren 1900 en 2000 nemen. 1900 is deelbaar door 100, maar niet tegen 400. Dus 1900 was geen schrikkeljaar.

Daarentegen, 2000 kan worden gedeeld door zowel 100 als 400, dus het bleef een schrikkeljaar, en wordt een "eeuwig schrikkeljaar" genoemd.

Dus aan het einde van de 19e eeuw de volgorde van de schrikkeljaren ging:1892, 1896, 1904, 1908. Maar aan het einde van de 20e eeuw, schrikkeljaren gingen zonder onderbreking door (1992, 1996, 2000, 2004).

Wat betekent dit? In de oude Juliaanse kalender, er waren 100 schrikkeljaren in elke 400 jaar. Maar in de Gregoriaanse kalender, we hebben er slechts 97 voor elke 400 jaar.

Dit geeft een opmerkelijk goede pasvorm voor de lengte van het tropische jaar. De gemiddelde lengte van één jaar in de 400-jarige Gregoriaanse cyclus is 365,2425 dagen. Dat is bijna (maar niet helemaal) precies één tropisch jaar - in feite de twee verschillen slechts 26,8 seconden van elkaar.

Dat is zo dichtbij dat we ons de komende duizenden jaren geen zorgen hoeven te maken dat onze seizoenen in de kalender verschuiven.

Dit artikel is opnieuw gepubliceerd vanuit The Conversation onder een Creative Commons-licentie. Lees het originele artikel.