
Wetenschap
Hoe moeilijk is het om Rubiks Cube te klauteren?

Rubik's Cube in de opgeloste staat. Krediet:Mike Gonzalez (TheCoffee)
Rubik's Cube is al 40 jaar een van 's werelds favoriete puzzels. Er zijn verschillende methoden bedacht om dit op te lossen, zoals uitgelegd in talloze boeken. Deskundige "speedcubers" kunnen het binnen enkele seconden oplossen.
Naast zulke staaltjes van verbazingwekkende behendigheid, er zijn veel fascinerende wiskundige vragen met betrekking tot Rubik's Cube. Een verplaatsing van de kubus bestaat uit het draaien van een van de zes vlakken met 90, 180, of 270 graden. Een duizelingwekkende 43, 252, 003, 274, 489, 856, 000 mogelijke toestanden kunnen worden verkregen door reeksen zetten toe te passen op de opgeloste toestand.
Ondanks deze complexiteit, in 2010 werd aangetoond dat Rubik's Cube altijd in 20 zetten of minder kan worden opgelost, ongeacht de begintoestand. Dit nummer wordt aangeduid als "Gods nummer, " aangezien alle bekende oplossingsmethoden die door mensen worden gebruikt doorgaans aanzienlijk meer zetten gebruiken dan deze optimale waarde.
Maar hoe zit het met de tegenovergestelde vraag:hoeveel zetten zijn er nodig om een opgeloste kubus door elkaar te gooien? Op het eerste gezicht, dit klinkt als een veel gemakkelijkere vraag dan het berekenen van Gods getal. Ten slotte, in tegenstelling tot het oplossen van een kubus, klauteren vereist geen enkele vaardigheid.
Soortgelijke vragen zijn met succes beantwoord voor het schudden van kaarten. Een beroemd voorbeeld is de studie uit 1990 van de "riffle shuffle" door wiskundigen Dave Bayer en Perci Diaconis. Een pak kaarten wordt gedefinieerd als "gemengd" als de volgorde willekeurig is, waarbij elke mogelijke volgorde dezelfde kans heeft om te verschijnen. Bayer en Diaconis toonden aan dat zeven riffle shuffles nodig en voldoende zijn om een standaard pak speelkaarten bij benadering te mengen.
Vorig jaar, wiskundigen publiceerden een soortgelijke studie van de 15 puzzel, die bestaat uit een vierkant van 4x4 gevuld met 15 schuiftegels en één lege ruimte.

Zakkubus in een vervormde staat. Krediet:Mike Gonzalez (TheCoffee)
Wat betekent het als een kubus door elkaar wordt gegooid?
Een typische persoon die een Rubik's Cube probeert te klauteren, zou er herhaaldelijk willekeurige bewegingen op uitvoeren. De resulterende willekeurige reeks toestanden is een speciaal geval van wat wiskundigen een Markov-keten noemen. De belangrijkste eigenschap is dat, gezien de huidige staat, de waarschijnlijkheid van wat de volgende toestand zal zijn, hangt niet af van een van de vorige toestanden.
De theorie van Markov-ketens toepassen op het klauteren van kubussen, hieruit volgt dat naarmate het aantal willekeurige zetten toeneemt, de kans om in een bepaalde van de mogelijke toestanden te zijn, wordt steeds dichter bij 1/43, 252, 003, 274, 489, 856, 000. Wiskundigen noemen dit een "uniforme kansverdeling, " aangezien elke mogelijke toestand met dezelfde waarschijnlijkheid optreedt.
Na een bepaald aantal willekeurige zetten, de staat van de kubus zal willekeurig zijn, maar de kansverdeling zal niet precies uniform zijn; sommige staten zullen vaker voorkomen dan andere.
Laten d(t) beschrijf hoeveel de kansverdeling na t willekeurige bewegingen verschilt van de uniforme kansverdeling. Als het aantal willekeurige zetten ( t ) neemt toe, de waarde van d(t) zal afnemen. De kubus die wordt vervormd komt overeen met: d(t) klein zijn.
Markov-keten Monte Carlo
In de theorie van Markov-ketens, deze afname in d(t) wordt "mengen" genoemd. Naast kaarten schudden en puzzelen, de theorie van Markov-ketenmenging heeft ook zeer serieuze praktische toepassingen. Een van de belangrijkste rekenhulpmiddelen in de moderne wetenschap en techniek is de Monte Carlo-methode. Deze methode, zoals het beroemde casino waarnaar het is vernoemd, berust in wezen op toeval. In essentie, het probeert harde wiskundige problemen bij benadering op te lossen met behulp van meerdere willekeurige gissingen.
In praktijk, Markov-ketens worden vaak gebruikt om deze willekeurige toestanden te produceren. Om de nauwkeurigheid van deze Markov-keten Monte Carlo-methoden te begrijpen, de belangrijkste taak is om in te schatten hoe snel d(t) neemt af als t neemt toe.
De zakkubus
Het bestuderen van het scrambling-probleem voor de standaard 3x3x3 Rubik's Cube is momenteel een fascinerende onopgeloste uitdaging. Echter, het wordt best beheersbaar als we onze aandacht richten op een kleinere 2x2x2-versie, de zakkubus genoemd.
In deze kubus de rand- en middenstukken ontbreken en alleen de hoekstukken blijven. De zakkubus heeft slechts 3, 674, 160 mogelijke staten, en het getal van God is slechts 11.
In de onderstaande grafiek, wij plotten d(t) voor de zakkubus. Na 11 zetten, d(t) is nog steeds erg groot, op 0,695. De eerste waarde van t dat levert een op d(t) waarde onder 0,25 (vaak "de mengtijd" genoemd in de kettingtheorie van Markov) is 19. Na 25 zetten d(t) is 0,092; na 50 zetten is het 0,0012; en na 100 zetten is het 0,0000017.
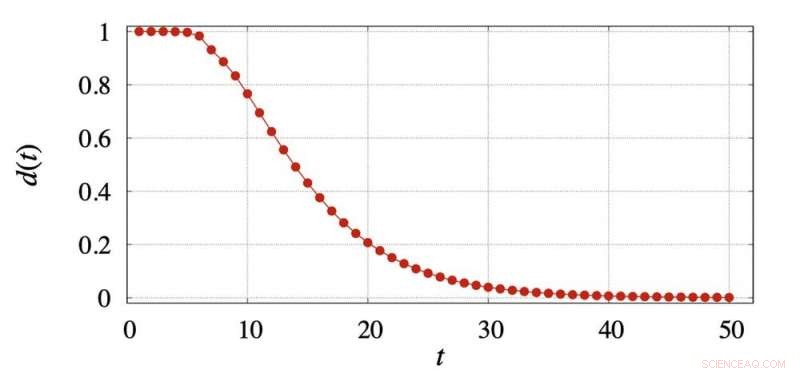
Afstand van de zakkubusverdeling van uniform na t-bewegingen. Krediet:Eric Zhou
Dus hoeveel zetten moet je gebruiken om een zakkubus volledig door elkaar te gooien? Het antwoord hangt af van hoe klein je zou willen d(t) zijn. Echter, het is zeker waar dat Gods aantal zetten onvoldoende is. Als een absoluut minimum, men mag niet minder dan 19 zetten gebruiken. Verdere details, inclusief code om te berekenen d(t) , zijn hier verkrijgbaar.
En uiteraard, als je eenmaal je kubus hebt vervormd, het enige wat je hoeft te doen is het weer op te lossen.
Dit artikel is opnieuw gepubliceerd vanuit The Conversation onder een Creative Commons-licentie. Lees het originele artikel. 
Hoofdlijnen
- Nieuwe aanpak kan de sleutel zijn tot de behandeling van antibioticaresistente bacteriën
- Waarom zijn botten belangrijk voor het lichaam?
- Model voorspelt hoe E. coli-bacteriën zich aanpassen onder stress
- Waarom wordt natrium gebruikt in DNA-extractie?
- Begrazingsbeheer voor vee compatibel met nestelende saliekorhoen
- Soorten genetische kruisen
- Waarom neemt het DNA-gehalte toe tijdens interfase?
- Dierenartsen verplegen zieke bobcat, breng het terug naar het park waar het nodig is
- Kunnen tweelingen elkaar voelen?
- Gestandaardiseerde maatregelen die nodig zijn om pleeggezinnen te screenen

- De eerste mensen in Tasmanië moeten spectaculaire aurora's hebben gezien

- Waarom vertrouwen essentieel is voor de volksgezondheidsstrategie

- Jura-dinosaurussen draafden tussen Afrika en Europa

- Versteende uitwerpselen onthullen vroege Krijt-diversiteit van aquatische gewervelde dieren

 Onderzoek identificeert alle verschillende manieren waarop de zee het menselijk welzijn ondersteunt
Onderzoek identificeert alle verschillende manieren waarop de zee het menselijk welzijn ondersteunt Rover detecteert oud organisch materiaal op Mars - en het zou een spoor van vorig leven kunnen zijn
Rover detecteert oud organisch materiaal op Mars - en het zou een spoor van vorig leven kunnen zijn Wetenschapsprojecten voor het testen van de sterkte van lijm
Wetenschapsprojecten voor het testen van de sterkte van lijm  VLA begint enorm project van kosmische ontdekking
VLA begint enorm project van kosmische ontdekking Een mogelijke verklaring voor verschillende metingen van de rotatiesnelheid van Venus
Een mogelijke verklaring voor verschillende metingen van de rotatiesnelheid van Venus Normaliteit in de chemie berekenen
Normaliteit in de chemie berekenen Een unitaire theorie van metrische analyse helpt bij het onthullen van structuren binnen gegevens
Een unitaire theorie van metrische analyse helpt bij het onthullen van structuren binnen gegevens Entertainment in de wachtruimte en samenwerking tussen fysieke winkels verhoogt de winst
Entertainment in de wachtruimte en samenwerking tussen fysieke winkels verhoogt de winst
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com


