
Wetenschap
Hoe ongelijkheid te meten als ervaren verschil?
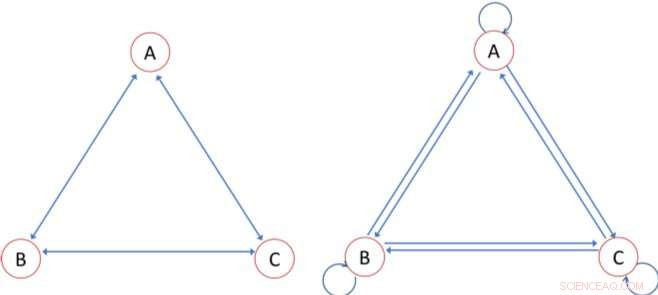
Ervaren verschillen (linker paneel) en de randen gebruikt in de conventionele maat (rechter paneel). Als knooppunten A, B, en C in figuur 1 hebben rijkdom 10, 4, en 3, bijvoorbeeld, de Gini-coëfficiënt met behulp van de netwerkweergave in het linkerdeelvenster is 0,412. Met behulp van de netwerkweergave aan de rechterkant, echter, de Gini wordt geschat op 0,274 Credit:Samuel Bowles en Wendy Carlin
Een nieuwe manier om ongelijkheid in rijkdom te meten, verklaart beter hoe we die ervaren. In een paper gepubliceerd in Economie Brieven , economen Samuel Bowles van het Santa Fe Institute en Wendy Carlin van University College London en het Santa Fe Institute stellen een nieuwe draai voor aan de veelgebruikte Gini-coëfficiënt - een werkpaard statistische maatstaf voor het meten van de kloof tussen haves en have-nots.
In een volkomen egalitaire samenleving, waar alle individuen even rijk zijn, de Gini-coëfficiënt moet 0 zijn. Omgekeerd, een samenleving waar een enkel individu alle rijkdom bezit, moet een Gini-coëfficiënt hebben die gelijk is aan 1. Met behulp van de Gini-coëfficiënt, landen kunnen worden gerangschikt van minst tot meest ongelijk.
Maar de rijkdom of het inkomen van individuen is niet het hele plaatje als het gaat om ongelijkheid. Volgens Bowles en Carlin, het standaardalgoritme voor het berekenen van Gini-coëfficiënten levert vreemde resultaten op, bijvoorbeeld wanneer een enkel individu alle rijkdom bezit, de Gini-coëfficiënt kleiner is dan 1, wat de waarde is die het zou moeten bereiken bij maximale ongelijkheid. Het corrigeren van die fout, ze laten zien, vereist een op het netwerk gebaseerde oplossing die de relaties tussen individuen in de samenleving verklaart.
"Sommige dimensies waarlangs ongelijkheid wordt gemeten, kunnen het best worden opgevat als individuele attributen, waarvan je gewoon meer of minder hebt, zoals hoogte, " legde Bowles uit. "Maar andere dimensies - zoals rijkdom - kunnen het best worden opgevat als verschillen tussen mensen in hun relaties met anderen."
Het linker netwerk in de afbeelding vertegenwoordigt de benadering van Bowles en Carlin, waarbij de pijlen die de knooppunten verbinden, ervaren sociale interacties vertegenwoordigen. Naar hun maat, het zijn de verschillen in rijkdom aan deze randen, niet de rijkdom van elk individueel knooppunt, wat de basis is van ervaren ongelijkheid. In hun krant Bowles en Carlin die ook de juiste Gini-coëfficiënt laten zien, wordt berekend uit de drie verschillen die verband houden met de drie randen in de figuur, en de gemiddelde rijkdom. Bijvoorbeeld, stel dat individu A een rijkdom heeft van 10, B heeft een vermogen van 4, en C heeft een rijkdom van 3. Dan is de correct gemeten Gini-coëfficiënt op basis van de verschillen langs de drie randen in de figuur links 0,41.
Het standaardalgoritme dat in het rechterdiagram in de afbeelding wordt geïllustreerd, telt het verschil tussen, zeggen, persoon A en B twee keer (de twee eenkoppige pijlen); maar er ontstaat een fout in het algoritme omdat het ook het "verschil" meet tussen de rijkdom van een individu en haar eigen rijkdom (de gebogen pijlen), die altijd nul is. Als resultaat, het standaardalgoritme onderschat de mate van ongelijkheid, wat een Gini-coëfficiënt van 0,27 oplevert voor dezelfde gegevens als hierboven.
De fout wordt pas merkbaar bij het werken met kleine populaties, zoals archeologen en biologen vaak doen. In het geval van Carlin een groep studenten in haar econ 101-klas wees haar op de fout toen ze een standaard online algoritme voor het berekenen van Gini-coëfficiënten toepasten op een probleemset. * Het algoritme dat ze online van Wolfram hadden gevonden, leverde verschillende antwoorden op voor voorbeelden met een klein aantal individuen van degene die zijn gevonden door de definitie toe te passen die het netwerkdiagram aan de linkerkant vertegenwoordigt.
Bowles en Carlin gebruiken ook verschillen in de netwerkstructuur om te kijken naar de beleving van ongelijkheid. Als de drie personen in het volledige netwerk (aan de linkerkant) in plaats daarvan in een rij zouden worden gerangschikt, met de rijkere in het midden, zoals een verhuurder met twee geïsoleerde pachters zou kunnen vertegenwoordigen, dan zonder verandering in de rijkdom van de drie individuen, de ongelijkheid die wordt ervaren langs de randen die de drie verbinden, zou stijgen van 0,41 tot 0,57.
Ze illustreren hun methode met behulp van sociale netwerkgegevens om ervaren ongelijkheid in een gemeenschap van boeren in Nicaragua in te schatten.
"Het oplossen van de vooringenomenheid van kleine aantallen is niet de belangrijkste bijdrage van ons artikel, " zegt Carlin. "Het is dat we een manier hebben geboden om ongelijkheid te begrijpen die consistent is met onze intuïties over hoe we economische ongelijkheden ervaren, dat is door een paarsgewijze vergelijking van het eigen vermogen of inkomen met dat van anderen."
 Wat voor soort onzichtbare vlekken detecteren Black Lights?
Wat voor soort onzichtbare vlekken detecteren Black Lights?  Een magnetische kurk voor het verwijderen van watervervuiling
Een magnetische kurk voor het verwijderen van watervervuiling Een laserfocus op het vinden van betere manieren om hernieuwbare brandstoffen te maken
Een laserfocus op het vinden van betere manieren om hernieuwbare brandstoffen te maken Hoe u het ionische percentage kunt berekenen zodra u het elektronegativiteitsverschil krijgt
Hoe u het ionische percentage kunt berekenen zodra u het elektronegativiteitsverschil krijgt Licht schijnend op de dynamiek van de aangeslagen toestand in perovskietmaterialen
Licht schijnend op de dynamiek van de aangeslagen toestand in perovskietmaterialen
 NASA's Groenland-missie verrast nog steeds in jaar vier
NASA's Groenland-missie verrast nog steeds in jaar vier Rekening houden met extreme regenval
Rekening houden met extreme regenval Opwarming van de aarde vermindert de betrouwbaarheid van weersvoorspellingstools
Opwarming van de aarde vermindert de betrouwbaarheid van weersvoorspellingstools Gegevens over ontgassing suggereren dat de Etna al maanden voor de uitbarsting van 2018 tekenen van drukopbouw begon te vertonen
Gegevens over ontgassing suggereren dat de Etna al maanden voor de uitbarsting van 2018 tekenen van drukopbouw begon te vertonen Bosbranden droegen bij aan recordverlies wereldwijd boombedekking
Bosbranden droegen bij aan recordverlies wereldwijd boombedekking
Hoofdlijnen
- Vijf belangrijke orgaansystemen van het lichaam
- Luipaarden doden minstens 3 kinderen op het Indiase platteland
- Wat zijn de functies van longblaasjes in de longen?
- Hoe virtuele geneeskunde werkt
- Wat zijn de verschillen tussen een centraal zenuwstelsel en een centraal zenuwstelsel?
- Hoe werkt het spierenstelsel met de bloedsomloop?
- Bodembedekkers verhogen de vernietiging van onkruidzaden in velden, licht werpen op interacties met roofdieren
- De Stoned Ape-hypothese:hebben paddo's de menselijke evolutie beïnvloed?
- Bepaling van allelfrequenties
- Hoe u uw kinderen kunt helpen met huiswerk - zonder het voor hen te doen

- Verbetering van de dialoog over de politieke kloof heen

- Naast vaccins, UNESCO wil dat meer wereldwijde wetenschap wordt gedeeld

- Nieuwe cognitieve vooringenomenheid die evaluatieprocessen beïnvloedt:het vrijgevigheid-erosie-effect

- Een manifest voor het onderzoeken van de impact van objectstromen op vroegere samenlevingen:Objectscapes
 Een evoluerend begrip van uitsterven
Een evoluerend begrip van uitsterven Hoe beïnvloedt inflatie de economie?
Hoe beïnvloedt inflatie de economie?  Een nieuw soort plastic dat zijn oorspronkelijke eigenschappen behoudt bij recycling
Een nieuw soort plastic dat zijn oorspronkelijke eigenschappen behoudt bij recycling Doorgaan met gestandaardiseerde tests kan meer problemen veroorzaken dan het oplost
Doorgaan met gestandaardiseerde tests kan meer problemen veroorzaken dan het oplost Emoji worden inclusiever, maar niet per se representatiever
Emoji worden inclusiever, maar niet per se representatiever Computermodel voorspelt hoe brekend metaalglas energie vrijgeeft op atomair niveau
Computermodel voorspelt hoe brekend metaalglas energie vrijgeeft op atomair niveau Nieuwe spinrichtingen in pyriet een bemoedigend teken voor toekomstige spintronica
Nieuwe spinrichtingen in pyriet een bemoedigend teken voor toekomstige spintronica Voordelen & nadelen van woestijnen
Voordelen & nadelen van woestijnen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

