
Wetenschap
We hebben een snellere manier gevonden om echt grote getallen te vermenigvuldigen

Als je dacht dat tafels van vermenigvuldiging op school moeilijk waren, stel je voor dat je getallen vermenigvuldigt met miljarden cijfers. Krediet:Shutterstock/Nina Buday
Vermenigvuldigen van twee getallen is eenvoudig, Rechtsaf?
Op de basisschool leren we als volgt lang vermenigvuldigen:
Methoden die vergelijkbaar zijn met deze gaan duizenden jaren terug, althans voor de oude Sumeriërs en Egyptenaren.
Maar is dit echt de beste manier om twee grote getallen met elkaar te vermenigvuldigen?
Bij lange vermenigvuldiging, we moeten elk cijfer van het eerste getal vermenigvuldigen met elk cijfer van het tweede getal. Als de twee nummers elk . hebben N cijfers, dat is N 2 (of N x N ) vermenigvuldigingen helemaal. In het bovenstaande voorbeeld N is 3, en we moesten 3 . doen 2 =9 vermenigvuldigingen.
Rond 1956, de beroemde Sovjet-wiskundige Andrey Kolmogorov vermoedde dat dit de best mogelijke manier om twee getallen met elkaar te vermenigvuldigen.
Met andere woorden, hoe je je berekeningen ook ordent, de hoeveelheid werk die u moet doen, is evenredig met ten minste N 2 . Twee keer zoveel cijfers betekent: vier keer zoveel werk.
Kolmogorov was van mening dat als een kortere weg mogelijk was, het zou toch al ontdekt zijn. Ten slotte, mensen vermenigvuldigen getallen al duizenden jaren.
Dit is een prachtig voorbeeld van de logische drogreden die bekend staat als "het argument uit onwetendheid".
Een snellere manier
Slechts een paar jaar later, Het vermoeden van Kolmogorov bleek spectaculair onjuist te zijn.
1960, Anatoly Karatsuba, een 23-jarige wiskundestudent in Rusland, ontdekte een stiekeme algebraïsche truc die het aantal benodigde vermenigvuldigingen vermindert.
Bijvoorbeeld, viercijferige getallen vermenigvuldigen, in plaats van 4 . nodig te hebben 2 =16 vermenigvuldigingen, Karatsuba's methode komt weg met slechts negen. Bij het gebruik van zijn methode, twee keer zoveel cijfers betekent alleen drie keer zoveel werk.
Dit levert een indrukwekkend voordeel op naarmate de aantallen groter worden. Voor getallen met duizend cijfers, De methode van Karatsuba heeft ongeveer 17 keer minder vermenigvuldigingen nodig dan lange vermenigvuldigingen.
Maar waarom zou iemand zulke grote getallen met elkaar willen vermenigvuldigen?
In feite, er zijn enorm veel toepassingen. Een van de meest zichtbare en economisch belangrijke is in cryptografie.
Grote aantallen in het echte leven
Elke keer dat u versleutelde communicatie op internet uitvoert, bijvoorbeeld toegang krijgen tot uw bankwebsite of een zoekopdracht op internet uitvoeren - uw apparaat voert een duizelingwekkend aantal vermenigvuldigingen uit, met getallen met honderden of zelfs duizenden cijfers.
Zeer waarschijnlijk gebruikt uw apparaat de truc van Karatsuba voor deze rekenkunde. Dit maakt allemaal deel uit van het verbazingwekkende software-ecosysteem dat ervoor zorgt dat onze webpagina's zo vlot mogelijk worden geladen.
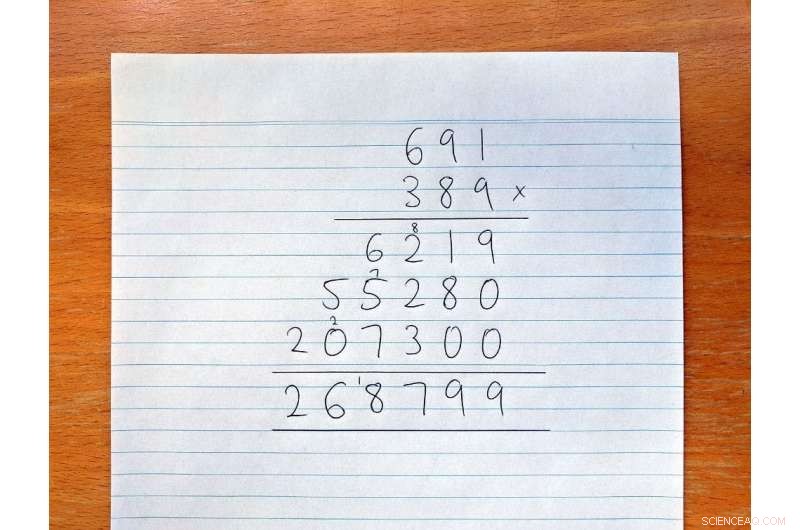
De lange weg naar vermenigvuldiging. Krediet:David Harvey
Voor wat meer esoterische toepassingen, wiskundigen hebben te maken met nog grotere getallen, met miljoenen, miljarden of zelfs biljoenen cijfers. Voor zulke enorme aantallen zelfs Karatsuba's algoritme is te traag.
Een echte doorbraak kwam er in 1971 met het werk van de Duitse wiskundigen Arnold Schönhage en Volker Strassen. Ze legden uit hoe ze de onlangs gepubliceerde snelle Fourier-transformatie (FFT) kunnen gebruiken om enorme getallen efficiënt te vermenigvuldigen. Hun methode wordt tegenwoordig routinematig gebruikt door wiskundigen om getallen in de miljarden cijfers te verwerken.
De FFT is een van de belangrijkste algoritmen van de 20e eeuw. Een bekende toepassing in het dagelijks leven is digitale audio:wanneer u naar mp3's luistert, muziekstreamingdiensten of digitale radio, FFT's zorgen achter de schermen voor de audiodecodering.
Een nog snellere manier?
In hun artikel uit 1971 Schönhage en Strassen maakten ook een opvallende gissing. Uitleggen, Ik moet even technisch worden.
De eerste helft van hun vermoeden is dat het mogelijk moet zijn om te vermenigvuldigen N -cijferige getallen met behulp van een aantal basisbewerkingen die evenredig zijn aan maximaal N log ( N ) (dat is N maal de natuurlijke logaritme van N ).
Hun eigen algoritme bereikte dit doel niet helemaal; ze waren te traag met een factor log (log N ) (de logaritme van de logaritme van N ). Hoe dan ook, hun intuïtie bracht hen ertoe te vermoeden dat ze iets misten, en dat N log ( N ) moet mogelijk zijn.
In de decennia sinds 1971, een paar onderzoekers hebben verbeteringen gevonden in het algoritme van Schönhage en Strassen. Opmerkelijk, een algoritme ontworpen door Martin Fürer in 2007 kwam pijnlijk dicht bij het ongrijpbare N log ( N ).
Het tweede (en veel moeilijkere) deel van hun vermoeden is dat: N log ( N ) zou de fundamentele snelheidslimiet moeten zijn - dat geen enkel mogelijk vermenigvuldigingsalgoritme beter zou kunnen doen dan dit.
Klinkt bekend?
Hebben we de limiet bereikt?
Een paar weken geleden, Joris van der Hoeven en ik hebben een onderzoekspaper gepost waarin we een nieuw vermenigvuldigingsalgoritme beschrijven dat uiteindelijk de N log ( N ) Heilige graal, daarmee de afwikkeling van de "gemakkelijke" deel van het vermoeden Schönhage-Strassen.
Het document is nog niet door vakgenoten beoordeeld, dus enige voorzichtigheid is geboden. Het is in de wiskunde gebruikelijk om onderzoeksresultaten te verspreiden voordat ze peer review hebben ondergaan.
In plaats van eendimensionale FFT's te gebruiken - het hoofdbestanddeel van al het werk aan dit probleem sinds 1971 - vertrouwt ons algoritme op multidimensionaal FFT's. Deze gadgets zijn niets nieuws:het veelgebruikte JPEG-beeldformaat is afhankelijk van 2-dimensionale FFT's, en 3-dimensionale FFT's hebben veel toepassingen in de natuurkunde en techniek.
In onze krant, we gebruiken FFT's met 1, 729 afmetingen. Dit is lastig te visualiseren, maar wiskundig niet lastiger dan het 2-dimensionale geval.
Werkelijk, echt grote cijfers
Het nieuwe algoritme is niet echt praktisch in zijn huidige vorm, omdat het bewijs in ons artikel alleen werkt voor belachelijk grote aantallen. Zelfs als elk cijfer op een waterstofatoom is geschreven, er zou bij lange na niet genoeg ruimte beschikbaar zijn in het waarneembare heelal om ze op te schrijven.
Anderzijds, we hopen dat met verdere verfijningen, het algoritme kan praktisch worden voor getallen met slechts miljarden of biljoenen cijfers. Als, het zou wel eens een onmisbaar instrument kunnen worden in het arsenaal van de computationele wiskundige.
Als het volledige vermoeden van Schönhage-Strassen correct is, dan vanuit een theoretisch oogpunt, het nieuwe algoritme is het einde van de weg - het is niet mogelijk om het beter te doen.
Persoonlijk, Het zou me verbazen als het vermoeden niet klopte. Maar we mogen niet vergeten wat er met Kolmogorov is gebeurd. Wiskunde kan soms voor verrassingen zorgen.
Dit artikel is opnieuw gepubliceerd vanuit The Conversation onder een Creative Commons-licentie. Lees het originele artikel. 
 Onderzoeksteam bewaart therapieën in poedervorm in proof-of-concept-experiment
Onderzoeksteam bewaart therapieën in poedervorm in proof-of-concept-experiment Fluorescentie-activerend bèta-vat-eiwit voor het eerst helemaal opnieuw gemaakt
Fluorescentie-activerend bèta-vat-eiwit voor het eerst helemaal opnieuw gemaakt Een chemische omhelzing van de perfecte gastheer
Een chemische omhelzing van de perfecte gastheer Lipiden: definitie, structuur, functie en voorbeelden
Lipiden: definitie, structuur, functie en voorbeelden Gezien de impact van de chemiecocktail voor binnenshuis
Gezien de impact van de chemiecocktail voor binnenshuis
 Prototypetechnologie voor het opgraven van mijnenvelden met vuur ontwikkeld door team
Prototypetechnologie voor het opgraven van mijnenvelden met vuur ontwikkeld door team vulkaan Bali slingert lava en as, luchthaven onaangetast
vulkaan Bali slingert lava en as, luchthaven onaangetast Planten spelen hoofdrol bij het rondpompen van giftig kwik door het milieu, onderzoekers zeggen:
Planten spelen hoofdrol bij het rondpompen van giftig kwik door het milieu, onderzoekers zeggen: Milieuproblemen in gematigde loofbossen
Milieuproblemen in gematigde loofbossen Nieuw vrijgegeven video toont man waarvan wordt aangenomen dat hij de laatste van de stam is
Nieuw vrijgegeven video toont man waarvan wordt aangenomen dat hij de laatste van de stam is
Hoofdlijnen
- Afbraak in het Noordpoolgebied
- Wilde druivengist kan effectiever zijn dan pesticiden bij het voorkomen van druivenschimmels
- Wat is nodig voor de glycolyse om te beginnen?
- Salamander-genoom geeft aanwijzingen over uniek regeneratief vermogen
- Fun Biology Presentatie Onderwerpen
- Wat is de evolutionaire betekenis van de genetische codes bij Universaliteit?
- Nieuwe minimaal invasieve procedure redt het leven van honden - en haar nier
- Wat betekent ion?
- Kunnen data dolfijnen redden? Hoe wetenschappers NASA-gegevens gebruiken om het verband tussen zonnestormen en het stranden van dieren te bestuderen
- Cyprus ontdekt eerste ongestoord Romeins scheepswrak

- Dinosaurussporen maken nieuwe indruk in Valley Forge park

- Uit nieuwe studie blijkt dat kunstwerken 35 procent minder waard zijn als ze zijn gemaakt door gemartelde kunstenaars

- Wiskundigen stellen nieuw ontwerp voor draadloze nanosensorische netwerken voor
- Ontwarren van de relaties tussen culturele kenmerken en andere variabelen
 Trash tracking-satellieten helpen Indonesië om afval in zee aan te pakken
Trash tracking-satellieten helpen Indonesië om afval in zee aan te pakken 10 echt slimme mensen die echt domme dingen deden
10 echt slimme mensen die echt domme dingen deden  Sommige zonnebrandmiddelen kunnen koralen doden. Moeten ze verboden worden?
Sommige zonnebrandmiddelen kunnen koralen doden. Moeten ze verboden worden? Chemici slagen erin aminoalcoholen te synthetiseren door gebruik te maken van licht
Chemici slagen erin aminoalcoholen te synthetiseren door gebruik te maken van licht De warmtestroom regelen met precisie op atomair niveau
De warmtestroom regelen met precisie op atomair niveau Stealth nanodeeltjes kunnen kankervaccins verbeteren
Stealth nanodeeltjes kunnen kankervaccins verbeteren Sneeuw boven Antarctica bufferde zeespiegelstijging vorige eeuw
Sneeuw boven Antarctica bufferde zeespiegelstijging vorige eeuw Een volledig beeld van de oorsprong en aard van zwerfvuil in de oceaan
Een volledig beeld van de oorsprong en aard van zwerfvuil in de oceaan
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

