
Wetenschap
Mobius caleidocycli:sensationele structuren met mogelijke toepassingen

Dr. Johannes Schönke en Prof. Eliot Fried creëerden een verscheidenheid aan Möbius Kaleidocycles met verschillende aantallen scharnieren van gevouwen papier en 3D-geprint materiaal. Krediet:OIST
Caleidocycli worden gevonden waar de wetenschap, wiskunde, en kunst ontmoeten. De objecten lijken op geometrische sculpturen die misschien in een museum voor moderne kunst te vinden zijn, maar het zijn de bewegingen die ze ondergaan die echt tot de verbeelding spreken. Ring koppelingen, opgebouwd uit scharnieren en strakke geometrische vormen, kan continu binnenstebuiten worden gekeerd, doet denken aan een bloemknop die steeds opnieuw bloeit. De betoverende objecten wekken verwondering op bij iedereen die ze ziet, inclusief nieuwsgierige ingenieurs en wiskundigen.
Onderzoekers van de Okinawa Institute of Science and Technology Graduate University (OIST) hebben nu een nieuwe klasse caleidocycli onthuld, een die volgens hen vooruitgang in fundamenteel onderzoek zou kunnen stimuleren, synthetische chemie, en zelfs robotica. Ze publiceerden een paper waarin de objecten werden beschreven, genaamd Möbius caleidocycli, op 17 december, 2018, in de Proceedings van de National Academy of Sciences .
"Een klassieke caleidocyclus gemaakt van zes driehoekige piramides kan op slechts één specifieke manier worden verplaatst, dus we waren geïnteresseerd in het vinden van andere ringverbindingen met die eigenschap - we wisten niet zeker of dergelijke objecten konden worden geconstrueerd, " zei Dr. Johannes Schönke, eerste auteur van de studie en een postdoctoraal wetenschapper in de OIST Mathematics, Mechanica, en Materiaaleenheid. Op basis van dit onderzoek, Schönke ontwierp een interactieve visualisatietool om de bewegingen van Möbius Kaleidocycles verder te verkennen. "Het feit dat uw tablet deze berekeningen gemakkelijk in realtime kan uitvoeren, toont aan dat we het probleem hebben kunnen distilleren tot een eenvoudig berekenbaar systeem."
"Dit werk valt onder het gebied dat bekend staat als kinematica, of de geometrie van beweging, " zei prof. Eliot Fried, senior auteur van de studie en hoofdonderzoeker van de onderzoekseenheid. "Een kinematisch resultaat is verreikend omdat het niet afhankelijk is van bepaalde materiaaleigenschappen."
Wiskunde ontmoet de oude kunst van het vouwen van papier
Met een paar precieze vouwen en wat lijm, een plat vel papier kan worden omgevormd tot een klassieke caleidocyclus. Het gerealiseerde object bestaat uit zes identieke driehoekige piramides die met elkaar verbonden zijn door scharnieren zoals die van een draaideur. Wanneer de twee uiteinden van deze keten van piramides met elkaar verbonden zijn, de hoek tussen aangrenzende scharnieren is precies 90 graden. Deze precieze relatie maakt het mogelijk voor klassieke caleidocycli om binnenstebuiten te keren met perfecte drievoudige symmetrie.
Een soortgelijke caleidocyclus kan worden opgebouwd uit acht driehoekige piramides, maar er is een addertje onder het gras:in plaats van op één bepaalde manier te roteren, een achtvoudige caleidocyclus kan op verschillende manieren bewegen. Deze extra "vrijheidsgraden" zorgen ervoor dat het object wankel beweegt, waardoor het minder bruikbaar is in toepassingen. Schönke en Fried vroegen zich af of ze een nieuwe caleidocyclus konden maken met zeven, acht, negen of meer elementen die nog steeds de klassieke enkele vrijheidsgraad behielden.
"We realiseerden ons al snel dat we moesten afstappen van het idee dat aangrenzende scharnieren haaks moeten staan, ’ zei Schönke.
Met behulp van wiskunde, computersimulaties, en zowel papieren als 3D-geprinte modellen, de onderzoekers realiseerden zich dat er voor elke caleidocyclus een speciale "draaihoek" bestaat, afhankelijk van het totale aantal links. Als de hoek tussen de scharnieren te klein is, de uiteinden van de ketting kunnen niet samengebracht worden om een gesloten ring te vormen. Als de hoek te groot is, het resulterende object zal extra vrijheidsgraden hebben en bewegen als een glibberige slang.
Fundamenteel onderzoek en toekomstige innovatie mogelijk maken
Schönke en Fried noemden hun creaties "Möbius kaleidocycles" in verwijzing naar een beroemd geometrisch object dat bekend staat als een Möbius-band. Je kunt je eigen Möbius-band maken door een rechthoekige strook papier te nemen, het ene uiteinde 180 graden draaien, en sluit het aan op het resterende uiteinde.
In tegenstelling tot een cirkelvormige ring gemaakt van dezelfde papieren strook, die twee verschillende zijden en randen zou hebben, een Möbiusband heeft slechts één zijde en één rand. Als u een pad volgt langs de middellijn van de band, je keert terug naar het beginpunt, maar aan de andere kant van de strook papier, allemaal zonder de rand van de band te overschrijden. Möbius Kaleidocycles delen deze topologie, en hebben daarom geen "bovenkant" of "onderkant". Möbius Kaleidocycles zijn als een Möbius-band gevormd met een draai van 540 graden, wat ook resulteert in een eenzijdige, enkelzijdig oppervlak.

Dr. Johannes Schönke en Prof. Eliot Fried hebben een nieuwe klasse van caleidocycli geïntroduceerd, die zeven of meer scharnieren hebben. Een van de grootste uitdagingen van de onderzoekers was om te leren aan welke voorwaarden moest worden voldaan om een keten van zeven of meer piramides (links) te sluiten in een ring (rechts). Krediet:OIST
Door hun unieke eigenschappen, Möbius kaleidocycles kunnen voor een breed scala aan toepassingen worden gebruikt. De onderzoekers stellen voor dat de objecten de basis kunnen vormen voor het ontwerpen van nieuwe mengmachines, energie overbrengende apparaten, of robotarmen. Individuele Möbius caleidocycles zouden kunnen worden ontworpen om te functioneren als zelfrijdende onderzeeërs, in staat om watermonsters te verzamelen of het leven in zee te volgen. De objecten kunnen ook worden samengevoegd om nieuwe inzetbare apparaten te maken - objecten die functioneren door van vorm te veranderen, zoals parasols of zonnepanelen op ruimteschepen.
"Een chemicus zou mogelijk moleculen kunnen synthetiseren op basis van Möbius-caleidocycli, " zei Schönke. "Omdat wrijving verwaarloosbaar is op moleculaire schaal, die moleculen zouden in wezen voor altijd kunnen roteren en zouden waarschijnlijk een extreem hoge warmtecapaciteit hebben."
Naast hun praktische toepassingen, Möbius caleidocycli roepen dwingende vragen op over fundamentele principes in de machinebouw, natuurkunde, en wiskunde.
"We hopen dat andere onderzoekers zullen worden geïnspireerd om die vragen te beantwoorden, " zei Fried, die ook opmerkte dat "dit werk ons ook in staat stelt een gemeenschap te betreden op het raakvlak van wiskunde, kunst en architectuur, wat op zich al spannend is."
 Licht vangen:hoe kobalt kan helpen zichtbaar licht te gebruiken om waterstofproductie uit water aan te drijven
Licht vangen:hoe kobalt kan helpen zichtbaar licht te gebruiken om waterstofproductie uit water aan te drijven Hoe de natuur waterstofproducerende enzymen bouwt
Hoe de natuur waterstofproducerende enzymen bouwt Gebruik van witte azijn en isopropylalcohol
Gebruik van witte azijn en isopropylalcohol  Microscoop voor mobiele telefoons detecteert de stille moordenaar van honingbijen
Microscoop voor mobiele telefoons detecteert de stille moordenaar van honingbijen Ontdekking van een oermetabolisch systeem dat ons een glimp geeft van de oorsprong van het leven op aarde
Ontdekking van een oermetabolisch systeem dat ons een glimp geeft van de oorsprong van het leven op aarde
 Japan keurt anti-plasticwet goed, maar zonder sancties voor vervuilers
Japan keurt anti-plasticwet goed, maar zonder sancties voor vervuilers Wereldwijde gletsjersmelt verhoogt de zeespiegel en put een ooit betrouwbare waterbron uit
Wereldwijde gletsjersmelt verhoogt de zeespiegel en put een ooit betrouwbare waterbron uit Nieuw rapport over klimaatverandering wordt waarschijnlijk tot de dood genegeerd
Nieuw rapport over klimaatverandering wordt waarschijnlijk tot de dood genegeerd Waterbeschikbaarheid bepaalt koolstofopname onder klimaatopwarming:studie
Waterbeschikbaarheid bepaalt koolstofopname onder klimaatopwarming:studie Voorwaardelijke toezeggingen kunnen Australië ertoe brengen zijn deel te doen aan klimaatverandering
Voorwaardelijke toezeggingen kunnen Australië ertoe brengen zijn deel te doen aan klimaatverandering
Hoofdlijnen
- Bijtkrachtonderzoek onthult dinosaurus-etende kikker
- Elements of Nucleic Acids
- Onderzoekers ontdekken slecht begrepen bacteriële lijnen in de monden van dolfijnen
- Turkije bevrijdt 7, 500 illegaal opgejaagde kikkers de rivier in
- De voordelen van Sticky End Enzymen
- Klimaatveranderingen verkorten de mariene voedselketen voor de kust van Californië
- Dierentuin Praag viert gezondheid zeldzame Maleise tijgerwelpen
- Langoustines hongeren naar kwallen gevangen op camera
- Hoe gender en stereotypen onze relatie met honden kunnen bepalen
- Archeologen ontdekken het vroegste bewijs van gedomesticeerde honden op het Arabisch Schiereiland

- Een 400 jaar oude gems zal als model dienen voor onderzoek naar ijsmummies

- De keerzijde van loyaliteit:onderzoek onthult waarom sommige organisatorische doofpotten niet worden gecontroleerd

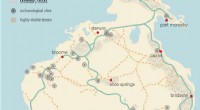
- Het in kaart brengen van de snelwegen die door de eerste Australiërs werden afgelegd
- Het verbeteren van de toegang tot fietsen kan vrouwen in gemarginaliseerde buurten ten goede komen

 Afbeelding:Rosettas steeds veranderende kijk op een komeet
Afbeelding:Rosettas steeds veranderende kijk op een komeet Polaire vortex tart klimaatverandering in het zuidoosten
Polaire vortex tart klimaatverandering in het zuidoosten Onderzoeker bestudeert effecten van wind nabij het oppervlak op landschapsevolutie
Onderzoeker bestudeert effecten van wind nabij het oppervlak op landschapsevolutie WISE J135501.90-825838.9 is een jonge, extreem lage massa substellaire binaire, studie vondsten
WISE J135501.90-825838.9 is een jonge, extreem lage massa substellaire binaire, studie vondsten Foto mijnbouw
Foto mijnbouw Een universele intercalatiestrategie voor zeer stabiele fotovoltaïsche perovskiet
Een universele intercalatiestrategie voor zeer stabiele fotovoltaïsche perovskiet Onderzoekers bevestigen dat de binnenkern van de aarde solide is
Onderzoekers bevestigen dat de binnenkern van de aarde solide is Verstrengeling van fotonen gegenereerd op miljoenen kilometers afstand
Verstrengeling van fotonen gegenereerd op miljoenen kilometers afstand
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

