
Wetenschap
Vijf manieren waarop het oude India de wereld veranderde - met wiskunde

Bakhshali-manuscript. Krediet:Bodleian-bibliotheken, Universiteit van Oxford
Het zou geen verrassing moeten zijn dat het eerste geregistreerde gebruik van het getal nul, onlangs ontdekt dat het al in de 3e of 4e eeuw is gemaakt, gebeurde in Indië. Wiskunde op het Indiase subcontinent heeft een rijke geschiedenis die meer dan 3 jaar teruggaat, 000 jaar en bloeide eeuwen voordat soortgelijke vorderingen werden gemaakt in Europa, met zijn invloed die zich ondertussen verspreidde naar China en het Midden-Oosten.
Naast het concept van nul, Indiase wiskundigen leverden baanbrekende bijdragen aan de studie van trigonometrie, algebra, rekenkundige en negatieve getallen onder andere gebieden. Misschien wel het belangrijkste, het decimale systeem dat we vandaag de dag nog steeds wereldwijd gebruiken, werd voor het eerst gezien in India.
Het nummersysteem
Al in 1200 voor Christus, wiskundige kennis werd opgeschreven als onderdeel van een grote hoeveelheid kennis die bekend staat als de Veda's. In deze teksten getallen werden gewoonlijk uitgedrukt als combinaties van machten van tien. Bijvoorbeeld, 365 kan worden uitgedrukt als driehonderd (3x10²), zes tientallen (6x10¹) en vijf eenheden (5x10⁰), hoewel elke macht van tien werd weergegeven met een naam in plaats van een reeks symbolen. Het is redelijk om aan te nemen dat deze weergave met machten van tien een cruciale rol heeft gespeeld in de ontwikkeling van het decimale waardesysteem in India.
Vanaf de derde eeuw voor Christus, we hebben ook schriftelijk bewijs van de Brahmi-cijfers, de voorlopers van de moderne, Indiaas of Hindoe-Arabisch cijfersysteem dat het grootste deel van de wereld tegenwoordig gebruikt. Toen nul werd ingevoerd, bijna alle wiskundige mechanica zou aanwezig zijn om de oude Indiërs in staat te stellen hogere wiskunde te studeren.
Het concept van nul
Zero zelf heeft een veel langere geschiedenis. De recent gedateerde eerste geregistreerde nullen, in wat bekend staat als het Bakhshali-manuscript, waren eenvoudige tijdelijke aanduidingen - een hulpmiddel om 100 van 10 te onderscheiden. Soortgelijke tekens waren al in de Babylonische en Maya-culturen in de vroege eeuwen na Christus en aantoonbaar in de Sumerische wiskunde al in 3000-2000 voor Christus.
Maar alleen in India werd het tijdelijke symbool voor niets een op zichzelf staand nummer. Door de komst van het nulconcept konden getallen efficiënt en betrouwbaar worden geschreven. Beurtelings, dit maakte een effectieve administratie mogelijk, waardoor belangrijke financiële berekeningen met terugwerkende kracht konden worden gecontroleerd, het waarborgen van de eerlijke acties van alle betrokkenen. Zero was een belangrijke stap op weg naar de democratisering van de wiskunde.
Deze toegankelijke mechanische hulpmiddelen voor het werken met wiskundige concepten, in combinatie met een sterke en open schoolse en wetenschappelijke cultuur, bedoelde dat, rond 600 na Christus, alle ingrediënten waren aanwezig voor een explosie van wiskundige ontdekkingen in India. In vergelijking, dit soort gereedschappen werden pas in het begin van de 13e eeuw populair in het Westen, hoewel Fibonnacci's boek liber abaci.
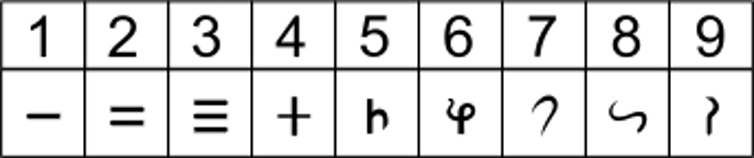
Brahmi-cijfers. Krediet:Wikimedia
Oplossingen van kwadratische vergelijkingen
In de zevende eeuw, de eerste schriftelijke bewijzen van de regels voor het werken met nul werden geformaliseerd in de Brahmasputha Siddhanta. In zijn baanbrekende tekst de astronoom Brahmagupta introduceerde regels voor het oplossen van kwadratische vergelijkingen (zo geliefd bij wiskundestudenten op de middelbare school) en voor het berekenen van vierkantswortels.
Regels voor negatieve getallen
Brahmagupta demonstreerde ook regels voor het werken met negatieve getallen. Hij verwees naar positieve getallen als fortuinen en negatieve getallen als schulden. Hij schreef regels op zoals:"Een fortuin afgetrokken van nul is een schuld, " en "een schuld afgetrokken van nul is een fortuin".
Deze laatste uitspraak is dezelfde als de regel die we op school leren, dat als je een negatief getal aftrekt, het is hetzelfde als het toevoegen van een positief getal. Brahmagupta wist ook dat "het product van een schuld en een fortuin een schuld is" - een positief getal vermenigvuldigd met een negatief is een negatief.
Voor het grootste deel, Europese wiskundigen waren terughoudend om negatieve getallen als zinvol te accepteren. Velen waren van mening dat negatieve getallen absurd waren. Ze redeneerden dat getallen waren ontwikkeld om te tellen en vroegen zich af wat je met negatieve getallen kon tellen. Indiase en Chinese wiskundigen erkenden al vroeg dat een antwoord op deze vraag schulden waren.
Bijvoorbeeld, in een primitieve landbouwcontext, als de ene boer 7 koeien schuldig is aan een andere boer, dan heeft de eerste boer effectief -7 koeien. Als de eerste boer eropuit gaat om dieren te kopen om zijn schuld terug te betalen, hij moet 7 koeien kopen en die aan de tweede boer geven om zijn aantal koeien weer op 0 te brengen. elke koe die hij koopt gaat naar zijn positieve totaal.
Basis voor calculus
Deze onwil om negatieve getallen aan te nemen, en inderdaad nul, hield de Europese wiskunde vele jaren tegen. Gottfried Wilhelm Leibniz was een van de eerste Europeanen die nul en de negatieven op een systematische manier gebruikte in zijn ontwikkeling van calculus aan het einde van de 17e eeuw. Calculus wordt gebruikt om de snelheid van veranderingen te meten en is belangrijk in bijna elke tak van wetenschap, met name ten grondslag liggen aan veel belangrijke ontdekkingen in de moderne natuurkunde.
Maar de Indiase wiskundige Bhāskara had 500 jaar eerder al veel van Leibniz' ideeën ontdekt. Bhaskara, leverde ook een belangrijke bijdrage aan de algebra, rekenkundig, geometrie en trigonometrie. Hij zorgde voor veel resultaten, bijvoorbeeld op de oplossingen van bepaalde "Doiphantine" vergelijkingen, die eeuwenlang in Europa niet zou worden herontdekt.
De Kerala-school voor astronomie en wiskunde, opgericht door Madhava van Sangamagrama in de jaren 1300, was verantwoordelijk voor vele primeurs in de wiskunde, inclusief het gebruik van wiskundige inductie en enkele vroege calculus-gerelateerde resultaten. Hoewel er geen systematische regels voor calculus werden ontwikkeld door de Kerala-school, de voorstanders bedachten eerst veel van de resultaten die later in Europa zouden worden herhaald, waaronder uitbreidingen van de Taylor-reeks, oneindigheden en differentiatie.
De sprong, gemaakt in India, die nul transformeerde van een eenvoudige tijdelijke aanduiding naar een op zichzelf staand getal, geeft de wiskundig verlichte cultuur aan die floreerde op het subcontinent in een tijd dat Europa vastzat in de donkere middeleeuwen. Hoewel zijn reputatie lijdt onder de eurocentrische vooringenomenheid, het subcontinent heeft een sterk wiskundig erfgoed, die het in de 21e eeuw voortzet door sleutelspelers te leveren in de voorhoede van elke tak van de wiskunde.
Dit artikel is oorspronkelijk gepubliceerd op The Conversation. Lees het originele artikel. 
 Nieuw onderzoek toont significante afname van gletsjers in West-Noord-Amerika
Nieuw onderzoek toont significante afname van gletsjers in West-Noord-Amerika Zeeniveau is een verrassend variabele parameter
Zeeniveau is een verrassend variabele parameter Nieuwe methode voor het onderzoeken van poriegeometrie in gesteenten
Nieuwe methode voor het onderzoeken van poriegeometrie in gesteenten Planten en samenleving verbinden:de verklaring van Shenzhen, een nieuwe roadmap voor plantenwetenschappen
Planten en samenleving verbinden:de verklaring van Shenzhen, een nieuwe roadmap voor plantenwetenschappen Decennia geleden lekt er nog steeds methaan uit de grond op de plaats van de gasexplosie
Decennia geleden lekt er nog steeds methaan uit de grond op de plaats van de gasexplosie
Hoofdlijnen
- Macht overdragen aan staten zal de bescherming van bedreigde diersoorten niet verbeteren
- Is het tijd dat ons begrip van evolutie evolueert?
- Hoe Agarose Gel te interpreteren
- Hoe schat ik de celgrootte met een microscoop?
- Waarom is bioinformatica belangrijk in genetisch onderzoek?
- Er zit een diepere vis in de zee
- Wetenschapsprojecten: roken en de effecten ervan op de longen
- DNA-klonen: definitie, proces, voorbeelden
- Een nieuw type robotmicroscoop
- Is er een impliciete gendervooroordeel op het gebied van economie?

- Bazen die alleen aan de bottom line denken, kunnen aanleiding geven tot onethisch gedrag

- Welke productcategorieën en sectoren profiteren het meest van sociale advertenties

- De Pinksterbeweging zoekt een gezondere vorm van gemeenschap

- Hoe verhoudingen uit te leggen

 Politieke blogs van tieners bevorderen tolerantie, participatie en publiek debat
Politieke blogs van tieners bevorderen tolerantie, participatie en publiek debat Apollo 12-astronaut Richard Gordon, die om de maan cirkelde, overlijdt
Apollo 12-astronaut Richard Gordon, die om de maan cirkelde, overlijdt Bananenplantenextract kan de sleutel zijn tot romiger, langer houdbaar ijs
Bananenplantenextract kan de sleutel zijn tot romiger, langer houdbaar ijs Een beter begrip van nanomaterialen
Een beter begrip van nanomaterialen Dissectie van de diepe aardbeving van Bonin in 2015
Dissectie van de diepe aardbeving van Bonin in 2015 Studiemodellen nieuwe methode om nanodeeltjes te versnellen
Studiemodellen nieuwe methode om nanodeeltjes te versnellen Lekke atmosfeer gekoppeld aan lichtgewicht planeet
Lekke atmosfeer gekoppeld aan lichtgewicht planeet IonQ kondigt ontwikkeling van volgende generatie kwantumcomputer aan
IonQ kondigt ontwikkeling van volgende generatie kwantumcomputer aan
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

