
Wetenschap
Wanneer Fock Landau ontmoet:topologie in atoom-foton-interacties
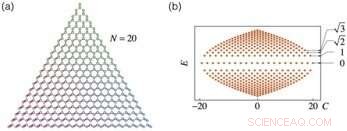
A. SL met plaatsafhankelijke koppelingssterkten. B. Energiespectrum van de FSL. Krediet:Science China Press
Sinds de ontdekking van het kwantum Hall-effect, topologische fasen van elektronen zijn een belangrijk onderzoeksgebied geworden in de fysica van de gecondenseerde materie. Veel topologische fasen worden voorspeld in roosters met specifieke engineering van elektronisch hoppen tussen roosterlocaties. Helaas, de afstand tussen aangrenzende locaties in natuurlijke roosters (kristallen) is in de orde van een miljardste van een meter, wat dergelijke engineering uiterst moeilijk maakt. Anderzijds, de fotonische kristallen hebben een veel grotere schaal. De eenheidscellen van fotonische kristallen voor zichtbaar licht zijn enkele duizenden malen groter dan die van elektronen. Daarom, het is niet verwonderlijk dat mensen hun toevlucht nemen tot fotonische analoog van topologische fasen door de overeenkomst tussen de Maxwell- en Schrodinger-vergelijkingen op te sporen, en een onderzoeksgebied genaamd topologische fotonica is tot bloei gekomen.
Echter, fotonen en elektronen zijn net zo verschillend als honden en katten. Fotonen zijn van nature sociaal. Ze houden ervan om bij elkaar te blijven (daarom hebben we lasers). Elektronen haten elkaar. Ze hebben hun eigen territoria volgens het Fermi-uitsluitingsprincipe. Topologische fotonica gebaseerd op de analogie tussen de Maxwell- en Schrodinger-vergelijkingen behoort tot de klassieke optica, d.w.z., een klassieke-golfsimulatie van de elektronische bandtopologie. Het is natuurlijk de vraag of gekwantiseerd licht nieuwe topologische fasen insluit die verder gaan dan de interpretatie van klassieke optica. Onlangs, Han Cai en Da-Wei Wang van de Zhejiang University onthulden de topologische fasen in roosters van gekwantiseerde lichttoestanden.
De energie van licht kan alleen bestaan in discrete verpakkingen, een niet-negatief geheel getal plus de helft van hν, waarbij h de constante van Planck is en ν de frequentie van het licht is. Het gehele getal is het aantal fotonen in die toestand, die de Fock-staat wordt genoemd, en de ene helft wordt bijgedragen door de vacuümfluctuaties. Deze discretie van lichtenergie is de sleutel om de spectra van de black-body-straling te verklaren (bijv. in een oven, hogere temperatuur verschuift de spectra naar de blauwe kant van een regenboogstrook). Lichtkwantisatie heeft ook ingrijpende gevolgen voor atoom-foton-interacties. Als er n fotonen in het lichtveld zijn, de kans dat een aangeslagen atoom nog een foton uitstraalt, is evenredig met n+1 (onthoud dat fotonen sociaal zijn en ze houden van nieuwe leden om mee te doen). Wanneer licht in een holte wordt opgesloten, de energie die door het atoom wordt uitgezonden, kan worden geresorbeerd, wat resulteert in een oscillatie van het atoom tussen de aangeslagen toestand en de grondtoestand, en de oscillatiefrequentie is evenredig met de vierkantswortel van n+1. Een spectrum van deze discrete waarden van de oscillatiefrequenties kan worden waargenomen wanneer het atoom is gekoppeld aan licht in een superpositie van Fock-toestanden, d.w.z., in het Jaynes-Cummings (JC)-model, die een standaardmethode is geworden voor het verkrijgen van de kwantumtoestanden van licht.
Het is niet duidelijk dat het JC-model gerelateerd is aan topologische fasen, maar deze vierkantswortel-van-geheel schaling van het energiespectrum doet denken aan de Landau-niveaus van elektronen in grafeen, die een bakermat is van topologische fasen. De energiebanden van elektronen in grafeen raken elkaar op twee punten aan de rand van de Brillouin-zone, noemde de Dirac-punten, waarbij de elektronen die de tweedimensionale Dirac-vergelijking gehoorzamen, een lineair verband hebben tussen de energie en het momentum. Wanneer een magnetisch veld wordt aangelegd, de elektronen maken cyclotronbewegingen met discrete frequenties die schalen met de vierkantswortel van gehele getallen, die overeenkomen met discrete Landau-niveaus. Cai en Wang legden de verbinding tussen het JC-model met drie modi en de Dirac-elektronen in een magnetisch veld.
In een JC-model met drie modi waarin een atoom is gekoppeld aan drie holtemodi, de kwantumtoestanden kunnen volledig worden beschreven door vier gehele getallen (x, ja, z, Q), waar x, y en z zijn de fotongetallen in de drie holtemodi, en q=0 en 1 voor de grond- en aangeslagen toestanden van het atoom. In het JC-model alle (N+1)^2 toestanden die voldoen aan x+y+z+q=N vormen een honingraatrooster, vergelijkbaar met een grafeen en we noemen het het Fock-state rooster. Aangezien het aangeslagen atoom een foton kan uitzenden naar een van de holtemodi, de staat (x, ja, z, 1) is gekoppeld aan drie aangrenzende staten, (x+1, ja, z, 0), (x, ja+1, z, 0) en (x, ja, z+1, 0). Echter, de koppelingssterkten aan de drie holtemodi zijn evenredig met de vierkantswortel van hun fotongetallen. Voor elke staat (x, ja, z, 1) er is een competitie tussen de drie holtes om het door het atoom uitgezonden foton te verkrijgen, en de holtes die meer fotonen bevatten hebben een voordeel, wat kan worden opgevat als het meerderheidsprincipe van fotonen. Dit komt overeen met een grafeen dat wordt onderworpen aan een spanning die de hopping-coëfficiënten van elektronen van de ene plaats naar de drie buren wijzigt.
Het blijkt dat wanneer de koppelingssterkte tussen de meest bevolkte holtemodus en het atoom groter is dan de som van die van de andere twee modi, de twee Dirac-punten komen samen en er ontstaat een band gap, wat een Lifshitz topologische overgang is tussen een halfmetaal en een bandisolator. In de halfmetaalfase, de variatie van de koppelingssterkte is gelijk aan een rekveld dat een effectief magnetisch veld induceert en leidt tot gekwantiseerde Landau-niveaus, op basis waarvan de auteurs het Valley Hall-effect hebben onderzocht en een Haldane-model hebben gebouwd in het JC-model met drie modi.
De auteurs onderzochten ook de eendimensionale Fock-state roosters met slechts twee holtemodi. Het zijn intrinsieke Su-Schriefer-Heeger-modellen en host-topologische randtoestanden. Het model kan verder worden uitgebreid tot meer dan drie dimensies voor topologische fasen die niet beschikbaar zijn in echte roosters. De voorgestelde topologische fasen zijn klaar om te worden gerealiseerd in supergeleidende circuits en zijn veelbelovend voor toepassingen in kwantuminformatieverwerking.
 Het spelalgoritme dat het materiaalontwerp zou kunnen verbeteren
Het spelalgoritme dat het materiaalontwerp zou kunnen verbeteren Wetenschappers onderzoeken racemasen en stellen strategieën voor om medicijnen te vinden die zich richten op deze belangrijke enzymen
Wetenschappers onderzoeken racemasen en stellen strategieën voor om medicijnen te vinden die zich richten op deze belangrijke enzymen Nieuw textiel kan je koel houden in de hitte, warm in de kou
Nieuw textiel kan je koel houden in de hitte, warm in de kou Laboratoriumtests tonen aan dat molecuul celdood in tumoren lijkt te stimuleren, ontsteking
Laboratoriumtests tonen aan dat molecuul celdood in tumoren lijkt te stimuleren, ontsteking Maakt het mogelijk om grotere 3D-geprinte objecten te maken met keramiek
Maakt het mogelijk om grotere 3D-geprinte objecten te maken met keramiek
 Afgewezen door compensaties:waarom sommige voorstanders twijfelen aan netto nultoezeggingen
Afgewezen door compensaties:waarom sommige voorstanders twijfelen aan netto nultoezeggingen Overstromingsgevoelige populaties met bijna 25% gestegen sinds 2000:studie
Overstromingsgevoelige populaties met bijna 25% gestegen sinds 2000:studie Wetenschappers pleiten voor uitgebreidere studies van Cascade-vulkanen
Wetenschappers pleiten voor uitgebreidere studies van Cascade-vulkanen Prijskaartje op de planeet? Zakelijk helpen de natuur te waarderen
Prijskaartje op de planeet? Zakelijk helpen de natuur te waarderen Nauwkeurigere schattingen van methaanemissies van melkvee ontwikkeld
Nauwkeurigere schattingen van methaanemissies van melkvee ontwikkeld
Hoofdlijnen
- Profase: wat gebeurt er in dit stadium van mitose en meiose?
- Waarom het zo moeilijk is om schepen bij te houden die niets goeds doen?
- Geluidsoverlast veroorzaakt chronische stress bij vogels, met gezondheidsgevolgen voor jongeren
- Wat is het verschil tussen gametogenese bij vrouwelijke zoogdieren en mannelijke zoogdieren?
- De oorsprong van genen voor het maken van bloemen
- CRISPR-octrooioorlogen benadrukken het probleem van het verlenen van brede intellectuele eigendomsrechten voor technologie die publieke voordelen biedt
- COVID-19 heeft de manier waarop we rouwen veranderd
- Wat is een Zygote?
- Mimetolieten:de gezichten die we zien in rotsformaties
 Autonome atoomassemblage van nanostructuren met behulp van een scanning tunneling microscoop
Autonome atoomassemblage van nanostructuren met behulp van een scanning tunneling microscoop 5 tips om je kinderen enthousiast te maken voor wiskunde
5 tips om je kinderen enthousiast te maken voor wiskunde November meteoren:Tauriden, Leoniden en een verrassende uitbarsting van Monocerotiden
November meteoren:Tauriden, Leoniden en een verrassende uitbarsting van Monocerotiden Apple-CEO overtuigd van vooruitzichten ondanks nee-zeggers
Apple-CEO overtuigd van vooruitzichten ondanks nee-zeggers Waarom vinden zoveel Amerikanen uit de arbeidersklasse dat politiek zinloos is?
Waarom vinden zoveel Amerikanen uit de arbeidersklasse dat politiek zinloos is? Eerste directe bandafstandmetingen van waterstof met brede kloof met behulp van inelastische röntgenverstrooiing
Eerste directe bandafstandmetingen van waterstof met brede kloof met behulp van inelastische röntgenverstrooiing Ingenieurs maken nieuw materiaal voor hoogwaardige supercondensatoren
Ingenieurs maken nieuw materiaal voor hoogwaardige supercondensatoren Experts:Fukushima moet meer doen om radioactief water te verminderen (update)
Experts:Fukushima moet meer doen om radioactief water te verminderen (update)
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com






