
Wetenschap
Onderzoek naar een dieper begrip en een betere beschrijving van netwerken
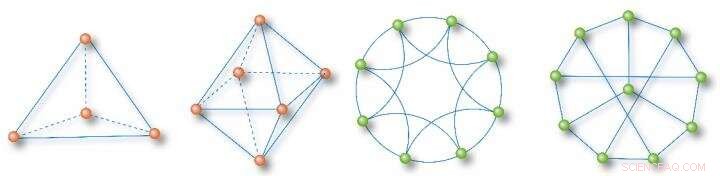
Volledig homogene netwerkvoorbeelden:een tetraëder, een minimaal netwerk met 2 caviteiten, een netwerk met 8 knooppunten, en een synchronisatie-optimaal netwerk met 10 knooppunten Credit:Science China Press
Sinds het begin van de vorige eeuw is onderzoek naar complexe systemen heeft de gebieden van chaos, fractals en netwerken. Een netwerk bestaat uit knooppunten en randen, waarbij knooppunten de elementen van een complex systeem vertegenwoordigen en randen de interacties daartussen beschrijven. Dergelijke knooppunt-randrelaties kunnen worden weergegeven door een aangrenzende matrix, waarvan de volgorde gelijk is aan het aantal knopen en elke rijsom correspondeert met een knoopgraad. De heterogeniteit van knooppuntgraden leidt tot de opkomst van stervormige structuren gecentreerd op knooppunten.
Om de heterogeniteit van knooppuntgraden aan te pakken, het schaalvrije netwerkmodel kwam in het spel, brede aandacht trekken. Daten, naarmate internettechnologie vordert en netwerkonderzoek vordert, onderzoekers hebben zich gerealiseerd dat de traditionele perceptie over op sterren gebaseerde heterogene netwerken onvoldoende is om evoluerende complexe netwerken en netwerkwetenschappelijke problemen te beschrijven. Bijvoorbeeld, er zijn veel online communities op internet die afhankelijk zijn van op fietsen gebaseerde sociale structuren voor groepscommunicatie en informatieverspreiding.
Netwerkfunctioneren en dynamische eigenschappen hebben meer en nauwere banden met topologische kenmerken van hogere orde, homogene substructuren en topologische invarianten. Dus, het verschuiven van de focus van knooppuntgraden naar cyclusnummers onthult veel volledig homogene subnetwerken in complexe netwerken. Hier, een volledig homogeen netwerk wordt gedefinieerd als een netwerk met knooppunten met dezelfde graad, dezelfde omtrek (aantal randen in de kleinste cyclus van een knoop), en dezelfde padsom (som van de kortste paden naar een knooppunt vanaf alle andere knooppunten). Een paar typische voorbeelden worden ter illustratie getoond in figuur 1.
Aan het einde van de 19e eeuw, Poincaré ontdekte dat grenzen de sleutel zijn bij het onderscheiden van geometrische vormen zoals schijven, sferen en tori. Hij ontleedde een geometrisch object in basiscomponenten die simplexen worden genoemd (punt, lijn, driehoek, tetraëder, enzovoort.), en introduceerde toen de concepten van homologiegroepering, Betti-getal en knooppunt-randcorrelatiematrix, en de Euler-Poincaré-formule, waaruit blijkt dat de alternatieve sommatie van simplexen gelijk is aan de alternatieve sommatie van Betti-getallen.
Het basisidee van Poincaré is om een complexe geometrische vorm te splitsen om de procedure voor een oplossing te vereenvoudigen. Dat lukte hem omdat er veel totaal homogene subnetwerken zijn, zoals driehoeken en tetraëders (aangeduid als kliekjes in de grafentheorie of simplexen in de topologie) in een complex netwerk. Het zijn basisstructuren voor het ondersteunen van netwerkfuncties, die verschillen van sterren, het zijn cycli. Met deze basiselementen het is mogelijk om een netwerk te beschrijven met behulp van een reeks vectorruimten over het binaire veld.
Bijvoorbeeld, de vectorruimte heeft randen als basis, met afmeting gelijk aan het aantal randen; de vectorruimte heeft driehoeken als basis, met een afmeting gelijk aan het aantal driehoeken, enzovoort. Aangezien de begrenzing van een driehoek uit randen bestaat, de twee aangrenzende vectorruimten en kan worden gecorreleerd via een grensoperator, en de grensmatrix kan worden gebruikt voor presentatie en analyse. De grensmatrix heeft een rijkere wiskundige inhoud en is nuttiger dan de aangrenzende matrix. Bijvoorbeeld, met behulp van de rangorde van de grensmatrix kan men het Betti-getal berekenen, een belangrijke invariant van het netwerk, dat is het aantal lineair onafhankelijke holtes van verschillende ordes in het netwerk, oprichting van een homologiegroep. Figuur 2 toont de relaties van enkele vectorruimten en hun corresponderende grensoperatoren.
In 2002, Xiaofan Wang en Guanrong Chen publiceerden het eerste criterium van netwerksynchronisatie. Het werd gevolgd door een reeks werken, waaronder de introductie van volledig homogene netwerken via optimalisatie door Dinghua Shi, Guanrong Chen en Xiaoyong Yan in 2013, waaruit blijkt dat het volledig homogene netwerk met een langere omtrek en een kortere padsom een betere synchroniseerbaarheid heeft tussen netwerken van dezelfde grootte. In aanvulling, in 2006, Linyuan Lü en Tao Zhou gebruikten de H-operator om de relatie tussen knoopgraad, H-index en kernelwaarde, vaststelling van de DHC-stelling. Bij het onderzoek van de cyclusindex, een belangrijk werk is de empirische studie van Bassett et al. in 2018 over het hersenfunctionele netwerk, waarin ze wezen op het belang van kliekjes en holtes in het functioneren van netwerken. Tenslotte, we hebben onlangs de nauwe relatie tussen Euler-karakteristieke getallen en netwerksynchroniseerbaarheid ontdekt.
Deze reeks belangrijke vooruitstrevende resultaten toont het belang en belang aan van interdisciplinair onderzoek in de natuurkunde, biologie en wiskunde. Gezien het feit dat deze nieuwe richting van netwerkstructuuranalyse met behulp van algebraïsche topologische hulpmiddelen veelbelovend is, de onderzoekers kozen ervoor om hun huidige paper te publiceren, "Volledig homogene netwerken, " in Nationale wetenschappelijke recensie .
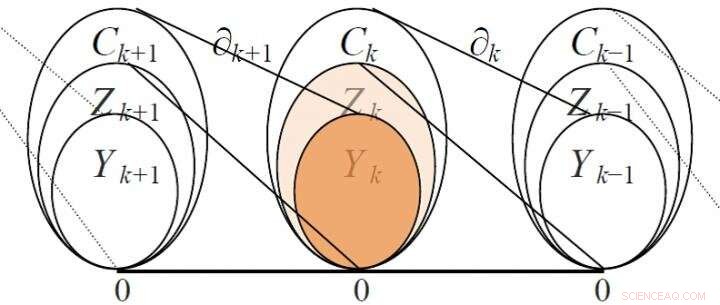
Relaties van enkele vectorruimten en hun corresponderende grensoperatoren (Zk is een cyclusgroep, Yk is een grensgroep) Credit:Science China Press
 Hoe de onthulling van de structurele ontwikkeling van zeolieten toekomstige synthetische ontwerpen ten goede zal komen
Hoe de onthulling van de structurele ontwikkeling van zeolieten toekomstige synthetische ontwerpen ten goede zal komen Franse wetenschappers beweren metallische waterstof te hebben gemaakt
Franse wetenschappers beweren metallische waterstof te hebben gemaakt Zonnecellen:het landschap van op cesium gebaseerde anorganische halide perovskieten in kaart brengen
Zonnecellen:het landschap van op cesium gebaseerde anorganische halide perovskieten in kaart brengen Kunstmatige intelligentie helpt bij de fabricage van materialen
Kunstmatige intelligentie helpt bij de fabricage van materialen Nadelen van kwalitatieve evaluatie in chemie-experimenten
Nadelen van kwalitatieve evaluatie in chemie-experimenten
 Klimaatactie dringend, zegt 's werelds enige waterambassadeur
Klimaatactie dringend, zegt 's werelds enige waterambassadeur Vijf redenen waarom de klimaatbesprekingen van de COP25 zijn mislukt
Vijf redenen waarom de klimaatbesprekingen van de COP25 zijn mislukt Aanpassingen van Lemurs
Aanpassingen van Lemurs Onderzoek suggereert dat economische groei gunstig is voor dieren in het wild, maar groeiende menselijke populaties niet
Onderzoek suggereert dat economische groei gunstig is voor dieren in het wild, maar groeiende menselijke populaties niet Voorjaar 2020 zou zelfs zomerzonrecords kunnen breken
Voorjaar 2020 zou zelfs zomerzonrecords kunnen breken
Hoofdlijnen
- Structurele inzichten in processen op DNA-schadeplekken
- Hoe kan licht virussen doden?
- Geërgerd door andere volkeren friemelen? Studie zegt dat je niet alleen bent
- Nieuwe genen op verslechterend Y-chromosoom
- Welke organen helpen het menselijk lichaam zich te ontdoen van verspillingen geproduceerd door cellen?
- Japanse walvisjagers naar Antarctica
- Wat zijn de verschillen tussen een plant en een dierlijke cel onder een microscoop?
- Nieuwe strategie zou bestaande medicijnen in staat kunnen stellen bacteriën te doden die chronische infecties veroorzaken
- Waarom lopen mensen meestal in dezelfde richting?
- Dubbele perovskieten in milieuvriendelijke zonnecellen

- Storing schakelt Google Agenda uit op desktopcomputers

- Luchtvaartmaatschappijen nemen geen risico met onze veiligheid - en kunstmatige intelligentie ook niet

- Ramadan in het Midden-Oosten is voor vasten en Facebook, gegevens laten zien

- Virtueel kampioenschap, echte ambitie nu NBA eSport-competitie lanceert

 Polen zegt dat oerwoud geen UNESCO-natuurerfgoed mag zijn
Polen zegt dat oerwoud geen UNESCO-natuurerfgoed mag zijn Boston, andere steden, werken aan het terugdringen van de kosten van hernieuwbare energie
Boston, andere steden, werken aan het terugdringen van de kosten van hernieuwbare energie Langzame doorvoer van sediment in het Australische Murray-Darling-riviersysteem verstoort het omgevingssignaal:studie
Langzame doorvoer van sediment in het Australische Murray-Darling-riviersysteem verstoort het omgevingssignaal:studie Onderzoekers ontwikkelen wereldwijde consensus over duurzaamheid in de gebouwde omgeving
Onderzoekers ontwikkelen wereldwijde consensus over duurzaamheid in de gebouwde omgeving Groene waterstof:roest als fotoanode en zijn grenzen
Groene waterstof:roest als fotoanode en zijn grenzen Typen en functies van condensatoren
Typen en functies van condensatoren  Afbeelding:Een sinister uitziend poollicht boven IJsland
Afbeelding:Een sinister uitziend poollicht boven IJsland Robotvloot duikt naar klimaatantwoorden in zeesneeuw
Robotvloot duikt naar klimaatantwoorden in zeesneeuw
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Swedish | German | Dutch | Danish | Norway | Portuguese |

-
Wetenschap © https://nl.scienceaq.com

