
Wetenschap
Wanneer is een aantrekkingskracht als een octopus?
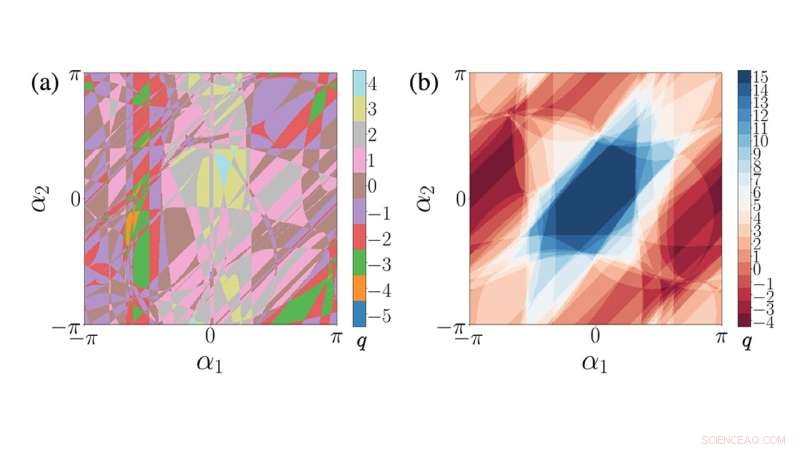
Krediet:Santa Fe Instituut
Wiskundigen die dynamische systemen bestuderen, richten zich vaak op de regels van aantrekking. Hoe beïnvloedt de keuze van het startpunt namelijk waar een systeem terechtkomt? Sommige systemen zijn gemakkelijker te beschrijven dan andere. Een slingerende slinger zal bijvoorbeeld altijd op het laagste punt landen, waar hij ook begint.
In dynamisch systeemonderzoek is een "bekken van aantrekking" de verzameling van alle startpunten - meestal dicht bij elkaar - die in dezelfde eindtoestand komen als het systeem zich in de loop van de tijd ontwikkelt. Voor eenvoudige systemen zoals een slingerende slinger is de vorm en grootte van een wastafel begrijpelijk. Niet zo voor meer gecompliceerde systemen:die met afmetingen die in de tientallen of honderden of hoger reiken, kunnen wilde geometrieën hebben met fractale grenzen.
Volgens nieuw werk van Yuanzhao Zhang, natuurkundige en SFI Schmidt Science Fellow, en Steven Strogatz, een wiskundige en schrijver aan de Cornell University, kunnen ze er zelfs uitzien als de tentakels van een octopus. De ingewikkelde geometrieën van deze hoogdimensionale bassins kunnen niet gemakkelijk worden gevisualiseerd, maar in een nieuw artikel gepubliceerd in Physical Review Letters , beschrijven de onderzoekers een eenvoudig argument dat aantoont waarom bassins in systemen met meerdere attractoren eruit zouden moeten zien als hoogdimensionale octopussen. Ze maken hun argument door een eenvoudig model te analyseren - een ring van oscillatoren die, ondanks dat ze alleen lokaal op elkaar inwerken, talloze collectieve toestanden kan produceren, zoals in-fase synchronisatie. Een groot aantal gekoppelde oscillatoren zal veel attractoren hebben, en dus veel bassins.
"Als je een hoogdimensionaal systeem hebt, domineren de tentakels de grootte van het bassin", zegt Zhang.
Belangrijk is dat het nieuwe werk laat zien dat het volume van een hoogdimensionaal bassin niet correct kan worden benaderd door een hyperkubus, hoe verleidelijk het ook is. Dat komt omdat de hyperkubus de overgrote meerderheid - meer dan 99% - van de punten in het bassin, die op tentakels zijn geregen, niet omvat.
Het artikel suggereert ook dat het onderwerp van hoog-dimensionale bekkens vol potentieel is voor nieuwe verkenning. "De geometrie is verre van alles wat we weten", zegt Strogatz. "Dit gaat niet zozeer om wat we hebben gevonden, maar om mensen eraan te herinneren dat er zoveel wacht om gevonden te worden. Dit is het vroege tijdperk van het onderzoeken van bekkens."
Het werk kan ook real-world implicaties hebben. Zhang wijst op het elektriciteitsnet als een voorbeeld van belangrijke hoogdimensionale systemen met meerdere aantrekkingsgebieden. Door te begrijpen welke uitgangspunten tot welke resultaten leiden, kunnen technici erachter komen hoe ze de lichten aan kunnen houden.
"Afhankelijk van hoe je je netwerk start, zal het ofwel evolueren naar een normale bedrijfstoestand of een storende toestand, zoals een black-out", zegt Zhang.
 Boliviaanse gletsjermonsters klaar voor wereldwijde ijsarchieven
Boliviaanse gletsjermonsters klaar voor wereldwijde ijsarchieven Kleine NASA-satelliet zal binnenkort regenbogen in wolken zien
Kleine NASA-satelliet zal binnenkort regenbogen in wolken zien Regeling voor duurzame gecertificeerde palmolie haalt doelen niet
Regeling voor duurzame gecertificeerde palmolie haalt doelen niet Welke instrumenten kunnen worden gebruikt om een overstroming te voorspellen?
Welke instrumenten kunnen worden gebruikt om een overstroming te voorspellen?
Dankzij weersvoorspellingstechnologie konden meteorologen mensen voorzien van kortetermijnvoorspellingen. Helaas betekent het simpelweg voorspellen van een onweersbui n
 Wat eet de harp zeehonden?
Wat eet de harp zeehonden?
Hoofdlijnen
- Hoe converteert ADP naar ATP?
- Vooruitgang bereikt in droge conservering van spermacellen van zoogdieren
- Welke cellen zou je gebruiken om DNA van een levende persoon te extraheren?
- Technologie verhoogt melkgift met 9 procent
- Studie meldt eerste bewijs van sociale relaties tussen chimpansees en gorilla's
- Verouderd DNA kan genen anders activeren
- Het huidige begrip van dierenwelzijn sluit momenteel vissen uit, ook al voelen vissen pijn
- Zo'n 230 walvissen gestrand in Tasmanië; reddingspogingen aan de gang
- Verrassend onderzoek bij apen vindt dat slechte tijden er niet toe leiden dat groepsleden hun gedrag veranderen
- Groot-Brittannië is een land van dierenliefhebbers - en dat hebben de Victorianen te danken

- Schaakstuk gevonden in Jordanië is misschien wel het oudste ter wereld

- In nieuw boek, geleerde biedt intiem portret van massale opsluitingen die de samenleving belasten

- Amerika's CO2-uitstoot steeg vorig jaar met 3,4 procent - ook al worden steenkoolcentrales afgesloten

- Schoolzonering kan de mate van beweging van adolescenten verhogen

 Studie:Biodiversiteit in stilstaande ondiepe meren remt de groei van waterplanten
Studie:Biodiversiteit in stilstaande ondiepe meren remt de groei van waterplanten Nieuw computermodel automatisch, foto's esthetisch bijsnijden
Nieuw computermodel automatisch, foto's esthetisch bijsnijden 5 enorm leuke weetjes over massa (geen gewicht)
5 enorm leuke weetjes over massa (geen gewicht) Studie:Dodelijk plastic afval nu gebruikelijk in Griekse walvissen
Studie:Dodelijk plastic afval nu gebruikelijk in Griekse walvissen Hoe het placebo-effect werkt
Hoe het placebo-effect werkt  Spuitbussen uit naaldbossen koelen het klimaat niet meer zo sterk
Spuitbussen uit naaldbossen koelen het klimaat niet meer zo sterk Uit Amazon-enquête blijkt dat meer dan de helft van de Amerikaanse werknemers zegt dat ze door het coronavirus onder werk zijn geraakt
Uit Amazon-enquête blijkt dat meer dan de helft van de Amerikaanse werknemers zegt dat ze door het coronavirus onder werk zijn geraakt Wat is een eenvoudige truss
Wat is een eenvoudige truss
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

