
Wetenschap
Om een onontgonnen gebied van harde problemen te onderzoeken, onderzoekers spelen advocaat van de duivel
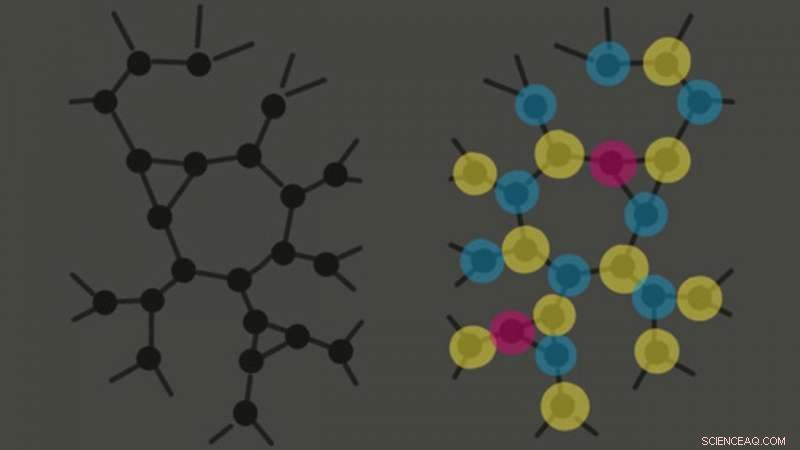
Kunnen algoritmen deze twee grafieken van elkaar onderscheiden? De uniforme grafiek aan de linkerkant is moeilijk te onderscheiden van de beplante oplossing aan de rechterkant. Krediet:Jess Banks, samenvattende presentatie op de 2021 Conference on Learning Theory
In de informatica, het grafiekkleurprobleem is een klassieker. Geïnspireerd door het kaartkleurprobleem, het vraagt:Gegeven een netwerk van knooppunten verbonden door links, wat is het minimum aantal kleuren dat je nodig hebt om elk knooppunt te kleuren, zodat er geen links zijn die twee van dezelfde kleur verbinden? Voor kleine aantallen kleuren en links, zoeken naar een oplossing is eenvoudig:probeer gewoon alle mogelijke combinaties. Maar naarmate de links toenemen, het probleem wordt beperkter - totdat, als er te veel links en niet genoeg kleuren zijn, er kan helemaal geen oplossing bestaan.
"Dan zijn er nog die fascinerende middenzones waar waarschijnlijk een oplossing ligt, maar het is heel moeilijk te vinden - en een andere waar die er waarschijnlijk niet is, maar het is moeilijk te bewijzen dat dat niet zo is, " zegt polymath Cris Moore, een resident professor bij SFI. Dat betekent dat conventionele probleemoplossende algoritmen ze niet kunnen vinden. hij zegt. Als men begint met een willekeurige kleuring, bijvoorbeeld, en begint gewoon de kleuren van knooppunten om te draaien, het zal een van deze verborgen oplossingen niet vinden.
In een nieuwe paper gepresenteerd op de 2021 Conference on Learning Theory, Moore en zijn medewerkers beschrijven een nieuwe manier om problemen te construeren met dergelijke verborgen oplossingen. De groep omvat wiskundige Jess Banks, een voormalige SFI-undergraduate en post-baccalaureaat stagiair die nu een Ph.D. aan de Universiteit van Californië-Berkeley.
Ze benaderen het probleem door een soort wiskundige advocaat van de duivel te spelen. In plaats van problemen op te lossen, ze verzinnen nieuwe, gecompliceerde - met oplossingen erin verborgen. "We nemen de witte hoed van de oplosser af, de oplossingsvinder, en we zetten de zwarte hoed op van de persoon die lastige problemen ontwerpt - bijna zoals cryptografie, " zegt Moore. "De oplossing is verborgen."
De onderzoekers bedachten een subtiele manier om oplossingen te verbergen, zegt Moor. En als ze deze problemen overdragen aan probleemoplossende algoritmen, de algoritmen komen leeg. "Als we problemen kunnen creëren die veel algoritmen niet kunnen oplossen, of zelfs vertellen of er een oplossing is, " zegt Moor, "dan hebben we sterk bewijs dat we de zone hebben gevonden waar deze problemen moeilijk zijn."
Het artikel bevat een stelling die aantoont dat meerdere families van algoritmen geen oplossingen kunnen vinden voor deze gegenereerde problemen. Dat betekent dat onderzoekers dichter dan ooit bij het identificeren van de fase-overgangsgrens van deze "harde" zone zijn, waarin het moeilijk is om oplossingen te vinden - of te bewijzen dat die er niet zijn.
Moore zegt dat de voortdurende inspanning om problemen nauwkeurig te identificeren voortkwam uit vermoedens in de natuurkunde die vragen hoe systemen veranderen naarmate ze meer beperkt worden.
"Ons avontuur, " hij zegt, "is geweest om deze vermoedens en berekeningen in de natuurkunde om te zetten in wiskundige bewijzen." En de enige manier om het veld vooruit te blijven duwen, hij zegt, is om een beroep te doen op de overlappende sterke punten van tools uit de wiskunde, natuurkunde, en informatica.
 NASA ziet het einde van tropische depressie 29W
NASA ziet het einde van tropische depressie 29W De tsunami in Alaska die golven veroorzaakte die zo hoog waren als de Space Needle van Seattle
De tsunami in Alaska die golven veroorzaakte die zo hoog waren als de Space Needle van Seattle Het beperken van de opwarming van de aarde kan miljoenen gevallen van knokkelkoorts voorkomen
Het beperken van de opwarming van de aarde kan miljoenen gevallen van knokkelkoorts voorkomen Ontzilting produceert meer giftig afval dan schoon water
Ontzilting produceert meer giftig afval dan schoon water Hoe de Japanse Olympische Spelen op basis van hernieuwbare energie het begin kunnen zijn van een wereldwijde race voor schone energie
Hoe de Japanse Olympische Spelen op basis van hernieuwbare energie het begin kunnen zijn van een wereldwijde race voor schone energie
Hoofdlijnen
- Parasieten van huisdieren die dieren in het wild wereldwijd aantasten
- Wat wordt er gebruikt om DNA op een specifieke locatie voor splitsing te knippen?
- Zijn getrouwde mensen gelukkiger dan alleenstaanden?
- De structuur en functie van spiercellen
- Voors en tegens van Forensic Science
- Wat zijn de functies van Triglyceride Phospholipid & Sterol?
- Biofysici ontrafelen de exacte vouwing van een enkel gen
- Cavendish redden:team kweekt 's werelds eerste ziekteresistente bananen in Panama
- Wat zijn enkele voor- en nadelen van het gebruik van DNA-analyse om rechtshandhaving bij criminaliteit te bevorderen?
- Naarmate de landbouw zich ontwikkelde, dat gold ook voor samenwerking - en geweld

- Tienden van een pond omrekenen naar Ounces

- Het verschil tussen staafdiagrammen en lijndiagrammen

- Van grotkunst tot klimaatchaos:hoe een nieuwe tijdlijn voor koolstofdatering onze kijk op de geschiedenis verandert

- Genen onthullen verwantschap tussen drie slachtoffers van het Mongoolse leger in het bloedbad van 1238
 Ultrakorte periode bruine dwerg ontdekt
Ultrakorte periode bruine dwerg ontdekt Instructies voor een eenvoudige mechanische grabber schoolproject
Instructies voor een eenvoudige mechanische grabber schoolproject Tandwielverhouding Berekeningen
Tandwielverhouding Berekeningen  Stoutmoedig groeien:Japanse astronaut bezorgd over groeispurt in de ruimte
Stoutmoedig groeien:Japanse astronaut bezorgd over groeispurt in de ruimte Systeem om ruimtestation te ontdoen van uitademingen van astronauten inspireert CO2-verwijdering op aarde
Systeem om ruimtestation te ontdoen van uitademingen van astronauten inspireert CO2-verwijdering op aarde Kia roept meer dan 500.000 voertuigen terug; airbags worden mogelijk niet opgeblazen
Kia roept meer dan 500.000 voertuigen terug; airbags worden mogelijk niet opgeblazen Draagt stop-and-search bij aan de verspreiding van COVID-19 in het VK?
Draagt stop-and-search bij aan de verspreiding van COVID-19 in het VK? Verschil tussen centimeters en meters
Verschil tussen centimeters en meters
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Swedish | German | Dutch | Danish | Norway | Portuguese |

-
Wetenschap © https://nl.scienceaq.com

