
Wetenschap
Wiskundige stelt een nieuw criterium voor voor het oplossen van de Boussinesq-vergelijkingen
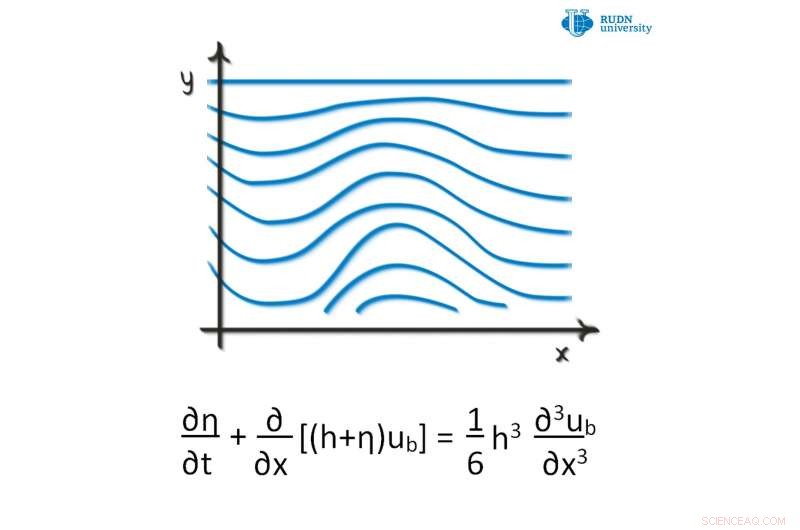
Krediet:RUDN University
Een wiskundige van de RUDN University heeft een nieuw criterium voorgesteld voor het oplossen van de Boussinesq-vergelijkingen. Deze vergelijkingen beschrijven de niet-lineaire voortplanting van golven in bepaalde media, bijv. plasma, een vloeistofoppervlak van geringe diepte, enzovoort. Ze onderzochten de Boussinesq-vergelijking in een driedimensionale ruimte en leidden een criterium af voor uniciteit en het bestaan van belangrijke oplossingen van een speciaal type voor de Boussinesq partiële differentiaalvergelijking. Het voorgestelde criterium heeft toepassingen in de mechanica van continue media, die de beweging van vloeistoffen en gassen bestudeert. Het artikel is gepubliceerd in Bulletin van de Braziliaanse Mathematical Society, Nieuwe series .
Zowel de Boussinesq-vergelijkingen als de Navier-Stokes-vergelijkingen zijn stelsels van partiële differentiaalvergelijkingen (differentiatie wordt uitgevoerd met betrekking tot alle onafhankelijke variabelen). Partiële differentiaalvergelijkingen spelen een belangrijke rol in de wiskundige natuurkunde en mechanica. Het oplossen van dit soort vergelijkingen is vaak erg moeilijk. Het probleem van het bestaan en de uniciteit van een oplossing voor de Boussinesq-vergelijkingen onder gegeven beginvoorwaarden (het zogenaamde Cauchy-probleem) was eerder door veel wetenschappers onderzocht, inclusief de auteurs van het artikel. Met bepaalde waarden van de parameters, de Boussinesq-vergelijkingen veranderen in Navier-Stokes-vergelijkingen. Het bestaan en de continue differentiatie, of, zoals wiskundigen zeggen, gladheid, van oplossingen voor de Navier-Stokes-vergelijkingen is een van de zeven millenniumprijsproblemen, gesteld in 2000 door het Clay Mathematics Institute.
Voor sommige functionele ruimtes (namelijk voor homogene Besov-ruimten, pf waarbij de beroemde Sobolev-ruimten een speciaal geval zijn), het probleem is met succes opgelost door de wiskundigen Don en Zhang. RUDN University wiskundige Maria Alessandra Ragusa en haar collega gingen verder, bewijst een soortgelijk criterium voor de Boussinesq-vergelijkingen in homogene Besov-ruimten. De auteurs onderzochten de Boussinesq-vergelijkingen in de driedimensionale ruimte, wat het mogelijk maakt om de resultaten vollediger toe te passen in de natuurwetenschappen.
Na een aantal noodzakelijke definities en aanvullende lemma's te hebben ingevoerd, de auteur van de RUDN University bewees met succes de hoofdstelling en toonde aan dat de oplossing voor het Cauchy-probleem niet alleen bestaat, is uniek, en heeft geen singuliere punten, maar breidt zich ook soepel uit tot een groter interval van een onafhankelijke variabele. Het artikel gebruikt het apparaat van functionele analyse, een wiskundige discipline met een hoog abstractieniveau. Hoe dan ook, dergelijke resultaten kunnen een brede en vruchtbare toepassing vinden in de mechanica en de natuurkunde.
 Chemici ontdekken het mechanisme van stralingsinstabiliteit van lithiumtetraboraat
Chemici ontdekken het mechanisme van stralingsinstabiliteit van lithiumtetraboraat Transistorfabricage op gebogen oppervlak betekent wenden tot betere diabetestherapie
Transistorfabricage op gebogen oppervlak betekent wenden tot betere diabetestherapie In een eerste, kleine diamanten aambeelden veroorzaken chemische reacties door erin te knijpen
In een eerste, kleine diamanten aambeelden veroorzaken chemische reacties door erin te knijpen Energie-efficiënte fotochemie op zonne-energie met luminescente zonneconcentratoren
Energie-efficiënte fotochemie op zonne-energie met luminescente zonneconcentratoren Onderzoeksteam maakt hydrogellijmen om wonden af te dichten
Onderzoeksteam maakt hydrogellijmen om wonden af te dichten
Hoofdlijnen
- Epigenetica legt uit waarom je DNA je lot niet voorspelt
- Hoe voeden bacteriën?
- Een 3D-model van een plantencel bouwen
- Algen kunnen planeet voeden en voeden met behulp van nieuwe hightech tool
- De controverse over het menselijk brein Nieuwe cellen maken
- De wetenschap achter waarom sommige mensen van dieren houden en anderen niets kan schelen
- Groenlandse walvissen komen naar Cumberland Sound in Nunavut om te exfoliëren
- Waarom we vleermuizen niet zo snel moeten demoniseren
- Hoe kan het gras op de greens op een golfbaan zo perfect zijn?
- Uit onderzoek blijkt dat bestuurders van flitsende auto's minder snel toegeven aan voetgangers

- Verkopers op websites met rubrieksadvertenties geven de voorkeur aan kopers uit welvarende buurten

- Onbetaalde verzorgers lijden honger tijdens COVID-lockdown, zegt onderzoek

- Hoe mannelijke porno-superfans echt naar vrouwen kijken

- Tandafdrukken en verloren tanden bieden inzicht in het eetgedrag van dinosauriërs
 Duitsland zou over 10 jaar de laatste gletsjers kunnen verliezen
Duitsland zou over 10 jaar de laatste gletsjers kunnen verliezen In 's werelds eerste, atoomkrachtmicroscoop ziet chemische bindingen in individuele moleculen (met video)
In 's werelds eerste, atoomkrachtmicroscoop ziet chemische bindingen in individuele moleculen (met video) Kritische vragen over ziekterisico's van plastic in de oceaan
Kritische vragen over ziekterisico's van plastic in de oceaan Schuif het, prik het, ANYmal haalt je afval op, wat er ook gebeurt
Schuif het, prik het, ANYmal haalt je afval op, wat er ook gebeurt India weegt verbod op populaire online game na sterfgevallen
India weegt verbod op populaire online game na sterfgevallen Paper:Schietpartijen op scholen beïnvloeden schoolkwaliteit, woningwaarde
Paper:Schietpartijen op scholen beïnvloeden schoolkwaliteit, woningwaarde Bevorderen van de veiligheid van diepgevroren voedsel:Cornell ontwikkelt een nieuwe tool voor de beoordeling van voedselveiligheid
Bevorderen van de veiligheid van diepgevroren voedsel:Cornell ontwikkelt een nieuwe tool voor de beoordeling van voedselveiligheid Facebook-bug heeft ten onrechte authentiek coronavirusnieuws verwijderd
Facebook-bug heeft ten onrechte authentiek coronavirusnieuws verwijderd
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | German | Dutch | Danish | Swedish | Norway |

-
Wetenschap © https://nl.scienceaq.com

