
Wetenschap
De dwingende wiskundige uitdaging van het drielichamenprobleem
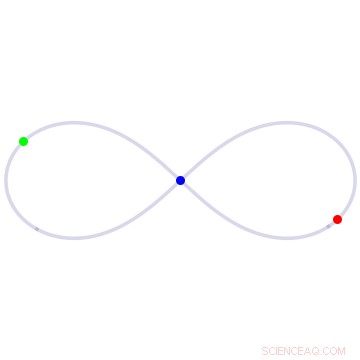
In de cijfer-acht-oplossing voor het drielichamenprobleem, drie lichamen van gelijke massa jagen elk rond een achtvormige lus. Krediet:Universiteit van Californië - Santa Cruz
Vanaf zijn oorsprong meer dan 300 jaar geleden in Newtons werk aan planetaire banen, het drielichamenprobleem is uitgegroeid tot een rijk onderwerp dat wiskundigen nog steeds nieuwe inzichten oplevert.
Richard Montgomery, een vooraanstaande professor in de wiskunde aan de UC Santa Cruz, noemt het een van de klassieke dilemma's in de wiskundige geschiedenis. In een artikel in het augustusnummer van Wetenschappelijke Amerikaan , hij vertelt over de geschiedenis van het drielichamenprobleem en de vooruitgang die hij en andere wiskundigen in de afgelopen twee decennia hebben geboekt.
"Het heeft mensen eeuwenlang uitgedaagd, en dat is deels wat het interessant maakt. Je voegt iets toe aan het werk van mensen als Newton en Poincaré en Lagrange, ' zei Montgomery.
Het fundamentele probleem is om de bewegingen te voorspellen van drie lichamen (zoals sterren of planeten) die wederzijds worden aangetrokken door de zwaartekracht, gezien hun beginposities en snelheden. Het blijkt dat een algemene oplossing voor het probleem in wezen onmogelijk is vanwege de chaotische dynamiek, die Henri Poincaré in 1890 ontdekte.
"Er zijn oplossingen voor speciale gevallen, maar er is geen simpele formule om je een algemene oplossing te geven, ’ legde Montgomery uit.
Vanuit het praktische oogpunt van het voorspellen van planetaire banen en het plannen van ruimtemissies, benaderingen kunnen met een hoge mate van nauwkeurigheid worden berekend met behulp van computers en een proces dat numerieke integratie wordt genoemd. Dat is misschien goed genoeg voor NASA, maar niet voor wiskundigen, wiens voortdurende verkenningen van het probleem hebben geleid tot belangrijke vooruitgang in de wiskunde.
Vallende katten
Het drielichamenprobleem verbindt drie verschillende takken van de wiskunde:topologie, geometrie, en dynamiek. Montgomery zei dat hij er meer dan 20 jaar geleden in geïnteresseerd was. Hij had gewerkt aan vragen met betrekking tot de wiskunde en natuurkunde van hoe een kat op zijn poten landt, die toepassingen heeft in regeltheorie en satellietoriëntatie.
"Ik bleef het probleem vereenvoudigen totdat de kat uit slechts drie puntmassa's bestond, " zei Montgomery. Toen verwees een collega hem naar een andere wiskundige die aan soortgelijke ideeën had gewerkt, en het duurde niet lang of hij was overgestapt van vallende katten naar hemelse mechanica. Toen ik hoorde dat de beste mensen die aan hemelmechanica werkten in Parijs waren, Montgomery bracht daar een sabbatical door met Alain Chenciner aan de Paris Diderot University aan het drielichamenprobleem.
Een van hun eerste grote resultaten, gepubliceerd in 2000, was een herontdekking en bewijs van een achtvormige oplossing, waarin drie lichamen van gelijke massa elkaar eindeloos achtervolgen rond een achtvormige lus. Hoewel Chris Moore van het Santa Fe Institute deze oplossing voor het eerst in 1993 had gevonden, met behulp van een numerieke benaderingsmethode, de herontdekking door Montgomery en Chenciner had een veel grotere impact op het veld.
"We waren in staat om een rigoureus bestaansbewijs te leveren van de cijfer-acht-oplossing, en door de manier waarop we het deden, konden anderen de oplossing veralgemenen en een heleboel andere interessante dingen vinden, ’ legde Montgomery uit.
Een meer algemene verklaring van het drielichamenprobleem voor elk aantal lichamen groter dan twee wordt het N-lichamenprobleem genoemd. Montgomery zei toen hij voor het eerst de driedelige 8-oplossing op een conferentie presenteerde, een lid van het publiek wees er snel op hoe het voor vier instanties zou moeten werken. Spoedig, wiskundigen ontdekten een gevarieerde reeks nieuwe banen voor het N-lichaamsprobleem met gelijke massa. Deze periodieke oplossingen waarin alle massa's elkaar achtervolgen rond een vast, gesloten curve zonder botsingen werden "choreografieën" genoemd door de Spaanse wiskundige Carles Simó, die er honderden heeft ontdekt.
"Het creëerde een mini-industrie, zodat we nu een groot aantal van deze choreografieën kennen, ' zei Montgomery.
Nieuwe richting
Jaren later, Simó hielp Montgomery's onderzoek naar het drielichamenprobleem in een nieuwe richting sturen door te suggereren dat hij op zoek zou gaan naar dynamische mechanismen die ten grondslag liggen aan de periodieke oplossingen. Dit leidde de afgelopen jaren tot een vruchtbare samenwerking met Rick Moeckel van de University of Minnesota.
De nieuwe wiskundige ideeën die zijn voortgekomen uit Montgomery's werk over het drielichamenprobleem hebben geen praktische toepassingen, tenminste nog niet. Het is vaak zo dat abstracte wiskundige concepten worden ontwikkeld lang voordat iemand ze praktisch kan gebruiken.
Veel mensen zijn gefascineerd door de esthetische aantrekkingskracht van de figuur-acht-oplossing en andere choreografieën. Het concept heeft zelfs zijn weg gevonden naar sciencefiction via de Chinese auteur Liu Cixin, wiens roman The Three-Body Problem in 2015 de Hugo Award won.
Maar Montgomery zegt dat hij het probleem nooit zou hebben aangepakt als hij geen vaste aanstelling had gehad.
"Het is zo'n moeilijk probleem, en je weet niet of je vooruitgang gaat boeken, " zei hij. "Maar volharding loont soms. Dus ik waardeer het tenure-systeem, en ook in staat zijn om sabbaticals te nemen om met medewerkers te werken. Er is iets aan het fysiek ontmoeten van mensen dat zo belangrijk is om samen te werken."
In zijn Wetenschappelijke Amerikaan artikel, Montgomery geeft niet alleen een gedetailleerde beschrijving van het drielichamenprobleem, maar ook een fascinerend verhaal over de internationale samenwerkingen en persoonlijke relaties die hem in staat stelden vooruitgang te boeken op dit meeslepende wiskundige raadsel.
 Beschrijf wat een fotosysteem doet voor fotosynthese
Beschrijf wat een fotosysteem doet voor fotosynthese Afbreekbare op suiker gebaseerde polymeren kunnen nuttige moleculaire vracht opslaan en vrijgeven
Afbreekbare op suiker gebaseerde polymeren kunnen nuttige moleculaire vracht opslaan en vrijgeven Onderzoekers ontwikkelen een optische vezel gemaakt van gel afgeleid van zeealgen
Onderzoekers ontwikkelen een optische vezel gemaakt van gel afgeleid van zeealgen Welke brandwonden heter: ethanol of methanol?
Welke brandwonden heter: ethanol of methanol?  Mobiele krachtcentrale recycleert afvalgassen
Mobiele krachtcentrale recycleert afvalgassen
 Wat op aarde? Fragmenten van oude oceaanbodem, Binnenmantel van de aarde geïdentificeerd in rotsen in het Baltimore-gebied
Wat op aarde? Fragmenten van oude oceaanbodem, Binnenmantel van de aarde geïdentificeerd in rotsen in het Baltimore-gebied Wuhans lockdown verminderde luchtvervuiling tot 63% - nieuw onderzoek
Wuhans lockdown verminderde luchtvervuiling tot 63% - nieuw onderzoek Hoe New York City zich voorbereidt op klimaatverandering
Hoe New York City zich voorbereidt op klimaatverandering NASA's ECOSTRESS detecteert Amazon-branden vanuit de ruimte
NASA's ECOSTRESS detecteert Amazon-branden vanuit de ruimte Meer dan 20, 000 hectare van de oudste Oekraïense bossen worden natuurlijke monumenten
Meer dan 20, 000 hectare van de oudste Oekraïense bossen worden natuurlijke monumenten
Hoofdlijnen
- De patronen van klimaatverandering
- 15 nieuwe gekkosoorten ontdekt in Myanmar
- Arctisch, grote visserslanden zijn het erover eens dat er niet gevist wordt in het noordpoolgebied, voor nu
- Genbewerking in de hersenen krijgt een grote upgrade
- Links of rechts? Net als mensen, bijen hebben een voorkeur
- Hoe beïnvloeden het uitsterven van andere wezens mensen direct?
- Wat zijn de belangrijkste functionele kenmerken van alle organismen?
- Hoe Spaced Repetition examen tijd een fluitje van een cent kan maken
- Grootschalige aanpak onthult imperfecte actor in plantenbiotechnologie
- De aanhoudende stadsvlucht

- Ten minste 2,6 miljoen Australiërs worden geconfronteerd met armoede wanneer de COVID-betalingen eindigen en de huurstress stijgt

- Vroege Pacific Islanders waren misschien de eerste natuurbeschermers

- Ziek totdat het gezond is gebleken:hoe de pandemie van COVID-19 de wereldwijde veiligheid verandert

- Gebruik van conservatieve en sociale media in verband met desinformatie over COVID-19
 Einde van de weg:Dyson stopt met race om elektrische auto's te maken
Einde van de weg:Dyson stopt met race om elektrische auto's te maken Ernstig geweld daalt met een derde in Engeland
Ernstig geweld daalt met een derde in Engeland Grote stappen voor het vastleggen van koolstof met behulp van aarde-overvloedige elementen als fotokatalytisch systeem
Grote stappen voor het vastleggen van koolstof met behulp van aarde-overvloedige elementen als fotokatalytisch systeem Nieuw bewijs suggereert dat het materie was die werd uitgestoten uit de Chicxulub-krater die leidde tot de impact op de winter
Nieuw bewijs suggereert dat het materie was die werd uitgestoten uit de Chicxulub-krater die leidde tot de impact op de winter Militarisering van de politie verbetert de veiligheid niet, kan de reputatie van de politie schaden
Militarisering van de politie verbetert de veiligheid niet, kan de reputatie van de politie schaden Beroemde meteoren
Beroemde meteoren  Na aardbevingen en overstromingen, Japan kiest ramp als symbool voor 2018
Na aardbevingen en overstromingen, Japan kiest ramp als symbool voor 2018 Aardbeving gevoeld in Massachusetts, Rhode Island
Aardbeving gevoeld in Massachusetts, Rhode Island
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway | French |

-
Wetenschap © https://nl.scienceaq.com

