
Wetenschap
Met deze vier eenvoudige stappen kun je een rekenwonder worden

Kun je het in dit wiskundige probleem knippen? Krediet:Sergey Lapin/shutterstock.com
Veel mensen vinden wiskunde een uitdaging. Als het waar is, dit stuk is voor jou. Als niet, dit stuk is nog steeds voor jou.
Waar denk je aan als je aan wiskunde denkt? Misschien denk je aan x'en en y's, hardnekkige breuken, of onzinnige woordproblemen. De cartoonist Gary Larson beeldde ooit af dat de bibliotheek van de hel alleen gigantische boekdelen met woordproblemen bevatte. Je weet wel, "Als een trein New York verlaat..."
Ik ben opgeleid als wiskundige, en ik zal je een handelsgeheim verklappen:dat is niet wat wiskunde is, noch waar het woont. Het is waar dat het leren van wiskunde vaak gepaard gaat met het oplossen van problemen, maar het moet gericht zijn op het plezier van het oplossen van puzzels, in plaats van regels te onthouden.
Ik nodig je uit om jezelf te zien als een probleemoplosser en wiskundige. En ik wil je graag voorstellen aan de man die me ooit uitnodigde voor de studie van probleemoplossing:George Pólya.
Math Pólya's manier
Om vele redenen, niet de minste daarvan is dat Pólya stierf in 1985, je zult hem ontmoeten zoals ik deed - via zijn enorm succesvolle 'How to Solve It'. Geschreven in 1945, van dit boek werden meer dan een miljoen exemplaren verkocht en het werd in 17 talen vertaald.
Als wiskundige, Pólya werkte aan een breed scala aan problemen, inclusief de studie van heuristieken, of hoe problemen op te lossen. Wanneer u leest "Hoe het op te lossen, " het voelt alsof je een rondleiding door Pólya's geest maakt. Dit komt omdat zijn schrijven metacognitief is - hij schrijft over hoe hij denkt over denken. En metacognitie is vaak de kern van het oplossen van problemen.
Het probleemoplossende plan van Pólya bestaat uit vier eenvoudige stappen:
- Zorg ervoor dat u het probleem begrijpt.
- Maak een plan om het probleem op te lossen.
- Voer het plan uit.
- Controleer je werk om je antwoord te testen.
Daar is het. Problemen oplossen in de palm van je hand - wiskunde teruggebracht tot vier stappen.
Hier is een klassiek probleem uit onderzoek naar wiskundeonderwijs gedaan door Jean Lave. Een man, laten we hem John noemen, maakt ¾ van een recept waarvoor 2/3 kopje kwark nodig is. Wat denk je dat John deed? Wat zou jij doen?
Als je bent zoals ik, je zou meteen in berekeningen kunnen duiken, misschien worstelen met wat de breuken betekenen, werken om de regels voor rekenen te onthouden. Dat is wat John leek te doen, aanvankelijk. Maar toen had hij een Eureka! moment.
John mat 2/3 kopje kwark, vervolgens op een snijplank gedumpt. Hij klopte de kaas in een cirkel en trok er lijnen in, een verticale, een horizontale, verdeel de kaastaart in vieren. Daarna duwde hij voorzichtig een kwart van de kwark terug in het bakje. Voila! Driekwart van 2/3 kopje kwark bleef over.
John is een wiskundige en probleemoplosser. Eerst, hij begreep het probleem:hij had ¾ nodig van wat het recept vereiste, dat was 2/3 kopje. Vervolgens, hij maakte een plan, hoogstwaarschijnlijk in zijn hoofd visualiserend hoe hij de kwark zou meten en verdelen. Eindelijk, hij voerde het plan uit.
Heeft hij zijn antwoord gecontroleerd? Dat blijft onduidelijk, maar we kunnen de geldigheid van zijn werk voor hem controleren. Heeft hij inderdaad ¾ van 2/3 kopje kwark gekregen? Ja, omdat het volledige bedrag met een kwart is verminderd, driekwart verlaten.
Een andere benadering
Zou deze oplossing werken met verschillende voedingsmiddelen of portiegroottes? Zolang iemand die portie in vieren kon verdelen, Ja, het plan zou werken.
Kunnen we het probleem op een andere manier oplossen met hetzelfde resultaat? Natuurlijk - er zijn veel manieren om dit probleem op te lossen, en ze zouden allemaal moeten resulteren in hetzelfde halve kopje antwoord. Hier is er een.
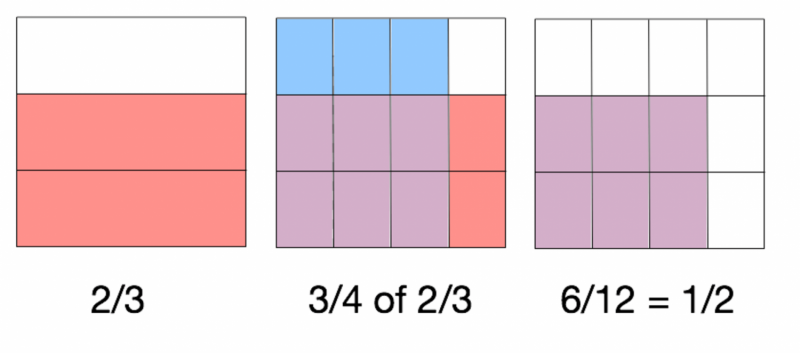
Hoe ¾ van 2/3 te vinden. Krediet:Jennifer Ruef, CC BY
Merk op dat deze oplossing afbeeldingen gebruikt. Nieuw hersenonderzoek bevestigt wat wiskundeleraren al decennia zeggen:afbeeldingen helpen ons denken. Tekenen is ook een van de suggesties van Pólya.
John heeft waarschijnlijk gebruik gemaakt van een van Pólya's belangrijkste suggesties:Kun je een gerelateerd probleem bedenken?
Natuurlijk, dit is een cheesy probleem - sorry, Ik heb niet eens geprobeerd om die woordspeling te bestrijden - wat een veelgehoorde klacht is over verhaalproblemen. Ik heb ervoor gekozen omdat het wiskundeonderzoekers al jaren in vervoering brengt, en omdat John heel slim is in zijn oplossing. Hij is ook extreem wiskundig.
Ik heb wiskunde gegeven, en hoe wiskunde te onderwijzen, al bijna 30 jaar. Al meer dan een decennium, het was mijn taak om eerstejaars op de middelbare school ervan te overtuigen dat algebra niet alleen zinvol was, maar dat het voor hen bedoeld was, en zij ervoor. In mijn werk, Ik heb veel mensen ontmoet die van wiskunde houden en velen die het overweldigend en onzinnig vinden. En dus is het een belangrijk onderdeel van mijn werk om mensen te helpen de schoonheid en het wonder van wiskunde te zien, en beschouwen zichzelf als wiskundigen.
Deze berichten zijn vooral belangrijk voor ouders die kinderen helpen wiskunde te leren. Als u het probleem begrijpt dat u probeert op te lossen, je bent goed op weg om het op te lossen. En jij, Ja jij, zijn een probleemoplosser.
We weten allemaal dat het niet altijd zo eenvoudig is om problemen op te lossen. Polya deed dat ook. Dat is de glorie ervan - de rommelige, prachtig, krachtig avontuur.
Dit artikel is oorspronkelijk gepubliceerd op The Conversation. Lees het originele artikel. 
 Welke van de metalloïden heeft de kleinste atoomradius?
Welke van de metalloïden heeft de kleinste atoomradius?  Nieuwe manier van testen op cocaïne ontdekt
Nieuwe manier van testen op cocaïne ontdekt Röntgenabsorptiespectra voorspellen uit grafieken
Röntgenabsorptiespectra voorspellen uit grafieken Bioplottering van bot-mimetische 3D-weefselsteigers met osteogene effecten
Bioplottering van bot-mimetische 3D-weefselsteigers met osteogene effecten Chemici ontwikkelen een nieuwe methode voor de synthese van polymere nanodeeltjes van een bepaalde grootte
Chemici ontwikkelen een nieuwe methode voor de synthese van polymere nanodeeltjes van een bepaalde grootte
 Consumenten zijn bereid te betalen voor ecosysteemdiensten
Consumenten zijn bereid te betalen voor ecosysteemdiensten Kan een aardbeving in Colorado zijn veroorzaakt door de impact van het uitsterven van dinosauriërs?
Kan een aardbeving in Colorado zijn veroorzaakt door de impact van het uitsterven van dinosauriërs? NASA-NOAA's Suomi NPP volgt vuur en rook van twee continenten
NASA-NOAA's Suomi NPP volgt vuur en rook van twee continenten Arctische overgang naar een nieuwe klimaatstaat
Arctische overgang naar een nieuwe klimaatstaat Schade door kanjer-orkanen die om vele redenen toenemen
Schade door kanjer-orkanen die om vele redenen toenemen
Hoofdlijnen
- Celsignalen die wondgenezing in gang zetten zijn verrassend complex
- Studie van gierende kraanvogels onthult een band tussen paren zelfs voordat ze de paringsleeftijd hebben bereikt
- Hoe een eenvoudige microscoop te maken
- Ethics of Genetic Engineering
- Hoe doodt alcohol bacteriën?
- Weefsels regenereren met moleculen die gericht zijn op genen
- Verschil tussen korrel- en agranulaire leukocyten
- Deze spitsmuizen hebben koppen die krimpen met het seizoen
- Voelen planten pijn?
- Steun Indonesiërs voor doodstraf neemt af met strengere onderzoeksmethoden

- Hoe consumenten in de supermarkt anders uitgeven in tijden van economische verandering

- Nieuwe manieren waarop wetenschappers kunnen helpen wetenschap terug in de populaire cultuur te brengen

- NYC parkstudie vergelijkt misdaadrapporten, gebruik kinderpark

- Hoe werkt zonnebrandcrème echt?

 Micropipetsonde voor het afstemmen van het volume en de deeltjesconcentratie van vloeistoffen
Micropipetsonde voor het afstemmen van het volume en de deeltjesconcentratie van vloeistoffen Teruggetrokken neutronenster gevonden in beroemde supernova
Teruggetrokken neutronenster gevonden in beroemde supernova Boeing stuurt Rosie-dummy naar de ruimte in een belangrijke missie zonder bemanning
Boeing stuurt Rosie-dummy naar de ruimte in een belangrijke missie zonder bemanning De effecten van klimaatverandering kunnen de politiek van militaire bases bemoeilijken, studie vondsten
De effecten van klimaatverandering kunnen de politiek van militaire bases bemoeilijken, studie vondsten Wat zijn de niveaus van organisatie in de biologie?
Wat zijn de niveaus van organisatie in de biologie?  Onderzoekers demonstreren nieuwe bouwsteen in quantum computing
Onderzoekers demonstreren nieuwe bouwsteen in quantum computing Soorten geleidbaarheid
Soorten geleidbaarheid  Scorpion Species Gevonden in Tennessee
Scorpion Species Gevonden in Tennessee
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- Italian | Spanish | Portuguese | Swedish | French | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

