
Wetenschap
Basis wiskundige symbolen uitgelegd

Belangrijkste punten
- De 11 basissymbolen die essentieel zijn voor het schrijven van wiskundige vergelijkingen zijn de plus (+), min (-), gelijk aan (=), is niet gelijk aan (≠), vermenigvuldiging (×), deling (÷), groter dan (> ), kleiner dan (<), groter dan of gelijk aan (≥), kleiner dan of gelijk aan (≤), breuk (/), decimaal (.) en procent (%) symbolen.
- Elk symbool heeft een specifieke functie en vormt de taal van de wiskunde.
- Het begrijpen van deze symbolen is cruciaal voor het oplossen van wiskundige problemen.
Gemeenschappelijke wiskundige symbolen geven ons een taal waarmee we alles kunnen begrijpen, van budgetteren tot de aard van de werkelijkheid zelf. De bouwstenen zijn relatief eenvoudig. Zelfs de meest geavanceerde wiskundige vergelijkingen zijn gebaseerd op een handvol fundamentele algemene wiskundige symbolen.
Voordat je het mysterie van het vermoeden van Collatz kunt oplossen, een vierkantswortel kunt berekenen of complexere algebraïsche symbolen kunt begrijpen, moet je de wiskundige basissymbolen beheersen. die nodig zijn voor het schrijven van een wiskundige vergelijking.
Inhoud
- Plus-symbool (+)
- Minteken (-)
- Is gelijk aan symbool (=)
- Is niet gelijk aan symbool (≠)
- Vermenigvuldigingssymbool (×)
- Deelsymbool (÷)
- Groter dan/kleiner dan-symbolen
- Groter dan of gelijk aan/kleiner dan of gelijk aan symbolen (≥ ≤)
- Breuksymbool (/)
- Decimaal symbool (.)
- Procentsymbool (%)
1. Plusteken (+)
Het plusteken (+) betekent optelling. Het is het meest elementaire wiskundige symbool ter wereld. Wanneer u twee of meer getallen optelt, gebruikt u het plusteken om aan te geven dat u ze combineert. 6 + 3 betekent bijvoorbeeld dat u positief getal 6 en positief getal 3 bij elkaar optelt. U kunt ook het plusteken vóór een getal plaatsen om aan te geven dat het getal positief is, hoewel dit doorgaans overbodig is; van een getal op zichzelf wordt aangenomen dat het positief is. Het schrijven van "+3" is niettemin een manier om duidelijk te maken dat u het over positief 3 heeft.
2. Minteken (-)
Het minteken (-) betekent aftrekken. Wanneer u het ene getal van het andere aftrekt, plaatst u het minteken ertussen. Met 6 - 3 geeft u bijvoorbeeld aan dat u 3 van 6 aftrekt. Net als bij het plusteken kunt u het minteken vóór een getal plaatsen om aan te geven dat het een negatieve waarde heeft. Dit komt veel vaker voor, omdat geschreven getallen niet standaard negatief zijn. Als u bijvoorbeeld '-3' schrijft, geeft dit aan dat u verwijst naar negatief 3.
3. Is gelijk aan symbool (=)
Het gelijkheidssymbool (=) geeft aan dat de waarden aan weerszijden van het symbool niet ongeveer gelijk zijn, maar volledig equivalent zijn. In de vergelijking 6 + 3 =9 geeft het gelijkteken aan dat de som van 6 en 3 gelijk is aan 9. Het gelijkteken is een essentieel onderdeel van elke wiskundige vergelijking.
4. Is niet gelijk aan symbool (≠)
Het 'is niet gelijk'-symbool (≠) geeft aan dat twee waarden niet zijn gelijkwaardig. Plaats dit teken tussen twee getallen of wiskundige uitdrukkingen die niet gelijkwaardig zijn. 6 ≠ 3 stelt bijvoorbeeld dat 6 niet gelijk is aan 3.
5. Vermenigvuldigingssymbool (×)
Het vermenigvuldigingssymbool (×) betekent het vermenigvuldigen van iets met iets anders, dat wil zeggen het vinden van het product van twee getallen of, om het anders te zeggen, het een bepaald aantal keren optellen van een getal bij zichzelf. Laten we dat duidelijk maken met een voorbeeld:6 × 3 =18 betekent dat je drie 6-en bij elkaar optelt, wat resulteert in een product van 18. Omdat het formele vermenigvuldigingssymbool (×) niet gebruikelijk is op toetsenborden, kun je een asterisk (* ) of een "x" in plaats daarvan. Dit is vooral handig bij het schrijven van computerprogramma's of Excel-formules.
6. Deelsymbool (÷)
Het deelsymbool (÷) geeft het delen van een getal aan. Dit is het proces waarbij een getal in een bepaald aantal gelijke delen wordt gesplitst. Beschouw de vergelijking 6 ÷ 3 =2. In dit voorbeeld wordt 6 verdeeld in 3 gelijke groepen van 2. Net als een van de andere belangrijke wiskundige objecten is het vermenigvuldigingssymbool, het formele symbool voor deling (÷), ongebruikelijk in het dagelijks gebruik. Wanneer u vergelijkingen typt, kunt u een schuine streep (/) gebruiken om deling aan te geven. Nogmaals, dit is nodig voor het schrijven van vergelijkingen in computerprogrammeertalen.

7. Groter dan/kleiner dan-symbolen
Het groter dan-symbool (>) en het kleiner dan-symbool (<) hebben niet dezelfde betekenis, maar geven aan dat de ene waarde groter is dan de andere. Deze symbolen functioneren op dezelfde manier als een gelijkheidssymbool tussen twee getallen. 6> 3 laat bijvoorbeeld zien dat 6 groter is dan 3, terwijl 3 <6 laat zien dat 3 kleiner is dan 6. Houd er rekening mee dat het grotere getal altijd naar het open uiteinde van het symbool wijst, terwijl het kleinere getal altijd naar het punt wijst waar de twee lijnen ontmoeten elkaar.
8. Groter dan of gelijk aan/kleiner dan of gelijk aan symbolen (≥ ≤)
Het symbool groter dan of gelijk aan (≥) en het symbool kleiner dan of gelijk aan (≤) combineren de symbolen groter dan en kleiner dan met het gelijk-symbool. Ze zijn gewend om, je raadt het al, aan te geven wanneer twee waarden groter (of kleiner) zijn dan of gelijk zijn aan elkaar. Dit symbool is niet erg gebruikelijk in het dagelijks gebruik, en komt het meest voor in vergelijkingen waarin een of meer grootheden onbekend zijn. In de vergelijking X ≥ 3 weten we bijvoorbeeld dat X 3 kan zijn of een willekeurig getal groter dan 3. In dit geval is 3 ≥ 3 een ware bewering, net als 4 ≥ 3, evenals 5 ≥ 3, en dus aan.
9. Breuksymbool (/)
Het breuksymbool (/) wordt weergegeven als een lijn of schuine streep die twee getallen onder elkaar scheidt. Het kan op een aantal verschillende manieren verschijnen. 3/5 betekent bijvoorbeeld drie vijfde. De 3 bovenaan de breuk staat op de positie van de teller, en de vijf onderaan de breuk staat op de positie van de noemer. Breuken laten zien hoeveel delen van een geheel je hebt; zeggen dat je 3/5 van een koekje hebt, betekent dat als een koekje in vijf gelijke delen is verdeeld, je 3 van die delen hebt. Voor ingewikkeldere wiskundige uitdrukkingen wordt het breuksymbool weergegeven als een lange horizontale lijn die de teller en de noemer scheidt.
10. Decimaal symbool (.)
Een decimaal (.) symbool is een puntsymbool dat wordt gebruikt om het hele deel van een getal te scheiden van het fractionele deel van een getal. Als dat een beetje verwarrend klinkt, laten we dan een stapje terug doen om het te begrijpen. Het getalsysteem is gebaseerd op een systeem van plaatswaarde , wat betekent dat de plaatsing van elk cijfer binnen een getal de waarde ervan aangeeft. In het getal 3.6 geeft de plaatsing van de 3 aan dat dit het hele deel van het getal is; de 6 staat rechts van de decimaal in wat wij de "tiendenplaats" noemen, wat betekent dat het 6/10 van 1 is. Als u 3,6 cookies had, zou u in totaal 3 en 6/10 cookies hebben. Extra cijfers na de komma hebben hun eigen plaatswaarde. In het getal 3.687 staat 8 op de honderdste plaats en 7 op de duizendste plaats.
11. Procentsymbool (%)
Net als het breuksymbool en decimaalteken is het procentteken (%) een van de belangrijkste wiskundige objecten, handig voor het weergeven van fractionele grootheden, in dit geval specifiek als een deel van 100. Als u 36% van de batterij van uw mobiele telefoon hebt, heeft u Nog 36 van de 100 eenheden batterijduur over. 'Procent' betekent 'van de honderd', en aangezien het procentteken (%) eruitziet als de opnieuw gerangschikte cijfers van 100, is het gemakkelijk te onthouden.
Dat is wiskundigDe plus (+) en min (-) wiskundige symbolen werden voor het eerst gebruikt in de 14e eeuw door Johannes Widman, de beroemde Duitse wiskundige. Hij publiceerde in 1489 het eerste gedrukte boek, getiteld 'Mercantile Arithmetic', waarin de tekens '+' en '-' werden gebruikt.
Veelgestelde vragen
Waarom zijn wiskundige symbolen universeel?
Wiskundige symbolen zijn universeel en zorgen voor duidelijke, beknopte en gestandaardiseerde communicatie tussen verschillende talen en culturen, waardoor het leren, onderwijzen en delen van wiskundige concepten gemakkelijker wordt.Hoe is het gebruik van symbolen geëvolueerd in de wiskundige geschiedenis?
Het gebruik van symbolen in de wiskunde is in de loop van de tijd aanzienlijk geëvolueerd, van het vroege gebruik van eenvoudige notaties voor basisbewerkingen tot de ontwikkeling van complexere symbolen voor abstracte concepten. Cement, zout en water:een nieuw opslagmateriaal voor groene warmte
Cement, zout en water:een nieuw opslagmateriaal voor groene warmte Kader om het pad van individuele koolstofatomen te volgen
Kader om het pad van individuele koolstofatomen te volgen Hoe een biofysische simulatiemethode het ontdekken van medicijndoelen kan versnellen?
Hoe een biofysische simulatiemethode het ontdekken van medicijndoelen kan versnellen? Naar autonome voorspelling en synthese van nieuwe magnetische materialen
Naar autonome voorspelling en synthese van nieuwe magnetische materialen Hoe Celsius converteren naar Kelvin
Hoe Celsius converteren naar Kelvin
 Bewijs opgraven:onderzoekers onderzoeken processen die bodemgezondheid ondersteunen
Bewijs opgraven:onderzoekers onderzoeken processen die bodemgezondheid ondersteunen Brandpreventie verbeteren door big data
Brandpreventie verbeteren door big data Het zal moeilijk zijn, maar we kunnen de wereld voeden met plantaardig eiwit
Het zal moeilijk zijn, maar we kunnen de wereld voeden met plantaardig eiwit Wetlands aan de rand van het veld alleen kunnen de dode zone van de Golf van Mexico niet herstellen, zeggen onderzoekers
Wetlands aan de rand van het veld alleen kunnen de dode zone van de Golf van Mexico niet herstellen, zeggen onderzoekers  Informatie over Giraffe Eyes
Informatie over Giraffe Eyes
Hoofdlijnen
- Hoe elektroforese te analyseren
- Meer dan een tiende van 's werelds terrestrische genetische diversiteit is mogelijk al verloren gegaan, zegt onderzoek
- De diversiteit aan gewassen ter wereld documenteren en beschikbaar maken
- Japan Fisheries Agency stelt voor de commerciële vangst van gewone vinvissen toe te staan
- Chimpansees in het wild wijzigen waarschuwingen op basis van wat anderen in hun groep al weten, studie vondsten
- Celmembraan Feiten
- Planning op meerdere schaalniveaus voor gezonde koralen en gemeenschappen
- Koud verbijsterde zeekoeien, zeeschildpadden opwarmen bij SeaWorld
- Droogte decimeert de belangrijkste katoenoogst in Texas
- Nat plasma maakt een plons van nanoformaat
- Magnetisatie in kleine componenten kan nu worden gefilmd in het laboratorium
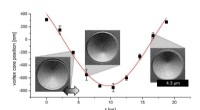
- Kleine microring-array maakt grote matrixvermenigvuldiging met complexe waarden mogelijk
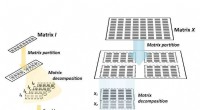
- Nieuw meerkanaals communicatiesysteem voor zichtbaar licht gebruikt één optisch pad
- Ingenieurs brengen laserpulsen naar nieuwe dimensies

 Is zure regen schadelijk voor dieren?
Is zure regen schadelijk voor dieren?  VS zoekt manieren om lithiumbatterijen in auto's te recyclen, telefoons
VS zoekt manieren om lithiumbatterijen in auto's te recyclen, telefoons Volkswagen laat Audi-chef vallen die wordt beschuldigd van dieselfraude
Volkswagen laat Audi-chef vallen die wordt beschuldigd van dieselfraude Een nieuwe perceptueel consistente methode voor visualisatie van massaspectrometriebeeldvorming
Een nieuwe perceptueel consistente methode voor visualisatie van massaspectrometriebeeldvorming Hoe horen dolfijnen?
Hoe horen dolfijnen?  Studie onthult dat gemeenten in Engeland moeite hebben om daklozen te huisvesten
Studie onthult dat gemeenten in Engeland moeite hebben om daklozen te huisvesten Oud aardewerk onthult het eerste bewijs voor de jacht op honing in prehistorisch West-Afrika
Oud aardewerk onthult het eerste bewijs voor de jacht op honing in prehistorisch West-Afrika Nieuwe bronnen van melaninepigment schudden ideeën over de kleur van fossiele dieren op
Nieuwe bronnen van melaninepigment schudden ideeën over de kleur van fossiele dieren op
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

