Een gemeenschap van materiaalfysici probeert dergelijke vragen te beantwoorden door te begrijpen wat er in materialen gebeurt, en hun gedrag te berekenen tot op het niveau van individuele elektroneninteracties en atomaire bewegingen.

Nu heeft een Caltech-team een ​​belangrijke ontdekking gedaan die dergelijke berekeningen helpt vereenvoudigen, waardoor ze met een factor 50 of meer worden versneld, terwijl de nauwkeurigheid behouden blijft. Als resultaat hiervan is het mogelijk om elektroneninteracties in complexere materialen en apparaten te berekenen en om nieuwe berekeningen te ontwikkelen die voorheen voor onmogelijk werden gehouden.

In een nieuw artikel gepubliceerd in het tijdschrift Physical Review X Yao Luo van Caltech, een afgestudeerde student toegepaste natuurkunde; zijn adviseur Marco Bernardi, hoogleraar toegepaste natuurkunde, natuurkunde en materiaalkunde; en collega's beschrijven een nieuwe datagestuurde methode die deze vooruitgang mogelijk heeft gemaakt. Hun aanpak vereenvoudigt de compacte rekenmatrices die worden gebruikt om de interacties weer te geven die plaatsvinden in een materiaal tussen elektronen en atomaire trillingen (of fononen, die kunnen worden gezien als individuele eenheden van trillingsenergie).

Luo en Bernardi zeggen dat de nieuwe methode hen in staat stelt slechts 1 tot 2% van de gegevens te gebruiken die doorgaans worden gebruikt om dergelijke problemen op te lossen, waardoor berekeningen aanzienlijk worden versneld en daarbij de belangrijkste interacties worden onthuld die de eigenschappen van materialen dicteren. P>

"Dit was heel verrassend", zegt Bernardi. "De elektron-fonon-interacties berekend met de gecomprimeerde matrices zijn bijna net zo nauwkeurig als de volledige berekening. Dit vermindert de rekentijd en het geheugengebruik enorm, in de meeste gevallen met ongeveer twee ordes van grootte. Het is ook een elegant voorbeeld van Occam's scheermes, de idee om de voorkeur te geven aan eenvoudige fysieke modellen met een minimaal aantal parameters."

Een nieuwe middenweg vinden voor het veld

Onderzoekers op dit gebied volgen over het algemeen een van twee benaderingen om materialen op dit meest fundamentele niveau te begrijpen. Eén benadering legt de nadruk op het bouwen van minimale modellen, waardoor de complexiteit van het systeem wordt verminderd, zodat onderzoekers een handvol parameters in pen-en-papierberekeningen kunnen aanpassen om een ​​kwalitatief inzicht in materialen te krijgen.

De andere begint met niets meer dan de structuur van een materiaal en maakt gebruik van zogenaamde 'eerste principes'-methoden (kwantummechanische berekeningen waarvoor grote computers nodig zijn) om materiaaleigenschappen met kwantitatieve nauwkeurigheid te bestuderen.

Deze laatste reeks methoden, waar de groep van Bernardi zich op richt, maakt gebruik van extreem grote matrices met miljarden ingangen om elektroneninteracties te berekenen die een breed scala aan fysieke eigenschappen controleren. Dat vertaalt zich in duizenden uren rekentijd voor elke berekening. Het nieuwe werk suggereert een soort middenweg tussen de twee benaderingen, zegt Bernardi.

"Met onze nieuwe methode kun je de grootte van deze matrices inkorten, de belangrijkste informatie eruit halen en minimale modellen genereren van de interacties in materialen."

De belangrijkste singuliere waarden eruit halen

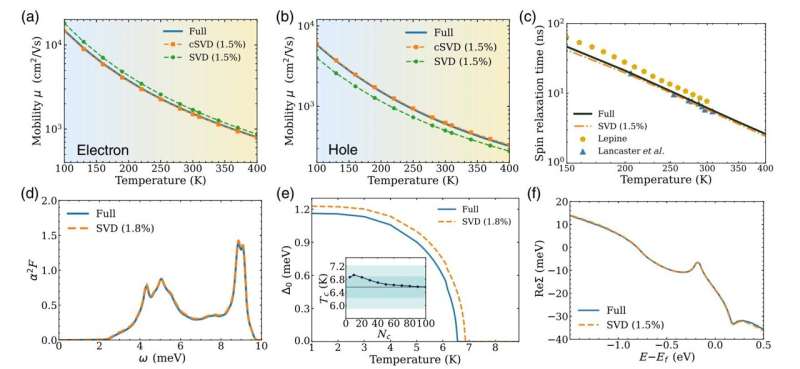
De aanpak van zijn groep is gebaseerd op het toepassen van een methode genaamd singular value decomposition (SVD) op de elektron-fonon-interacties in een materiaal. De SVD-techniek wordt veel gebruikt op gebieden als beeldcompressie en kwantuminformatiewetenschap. Hier kunnen de auteurs de elektronische en vibrerende componenten in een matrix van duizenden of miljoenen elektron-fonon-interacties scheiden of ontwarren en aan elke fundamentele interactie een nummer toekennen.

Deze echte positieve getallen worden singuliere waarden genoemd en rangschikken de fundamentele interacties in volgorde van belangrijkheid. Vervolgens kan het programma op een paar procent na alle interacties in elke matrix elimineren, waardoor alleen de leidende enkelvoudige waarden overblijven, een proces dat de bepaling goedkoper maakt met een factor die evenredig is aan de hoeveelheid compressie.

Dus als het programma bijvoorbeeld slechts 1% van de singuliere waarden bewaart, wordt de berekening met een factor 100 sneller. De onderzoekers hebben ontdekt dat het bij benadering behouden van slechts een klein deel van de singuliere waarden, doorgaans 1 tot 2%, het resultaat is behoudt bijna dezelfde nauwkeurigheid als de volledige berekening.

"Door SVD te gebruiken, kun je het aantal singuliere waarden terugdringen en alleen de hoofdkenmerken vastleggen van de matrices die elektronische interacties in een bepaald materiaal vertegenwoordigen", zegt Luo, hoofdauteur van het artikel en in zijn derde jaar in Bernardi's groep.

"Dit verkort de oorspronkelijke matrix, waardoor het algoritme wordt versneld, en heeft als bijkomend voordeel dat het onthult welke interacties in het materiaal dominant zijn."

Bernardi merkt op dat dit laatste voordeel van de SVD-methode de onderzoekers een "fysieke intuïtie" geeft over elektroneninteracties in een materiaal, iets dat in het verleden ontbrak in de berekeningen van de eerste principes. Bij een berekening met silicium werd het bijvoorbeeld duidelijk dat de dominante singuliere waarde verband hield met het uitrekken en samenknijpen van een bepaalde binding.

"Het is iets simpels, maar voordat we de berekening deden, wisten we niet dat dit de sterkste interactie was", legt Bernardi uit.

In het artikel laten de onderzoekers zien dat de compressie van matrices gerelateerd aan elektron-fonon-interacties met behulp van de SVD-methode nauwkeurige resultaten oplevert voor verschillende eigenschappen van materialen die onderzoekers mogelijk willen berekenen, waaronder ladingstransport, spin-relaxatietijden en de overgangstemperatuur van supergeleiders. .

Bernardi en zijn team breiden de op SVD gebaseerde berekeningen uit naar een breder scala aan interacties in materialen en ontwikkelen geavanceerde berekeningen die voorheen voor onmogelijk werden gehouden. Het team werkt ook aan het toevoegen van de nieuwe SVD-methode aan zijn open source Perturbo-code, een softwarepakket waarmee onderzoekers kunnen berekenen hoe elektronen op elkaar inwerken en bewegen in materialen. Bernardi zegt dat dit gebruikers in de wetenschappelijke gemeenschap in staat zal stellen materiaaleigenschappen die verband houden met elektron-fonon-interacties aanzienlijk sneller te voorspellen.

Het artikel is getiteld "Datagestuurde compressie van elektron-fonon-interacties." Samen met Luo en Bernardi zijn co-auteurs van het artikel onder meer afgestudeerde student Dhruv Desai (MS '22); Benjamin Chang (MS '20) en Jinsoo Park (Ph.D. '22), die nu postdoctoraal onderzoeker is aan de Universiteit van Chicago.