
Wetenschap
Waarom zijn optische brekingsindices zo klein?
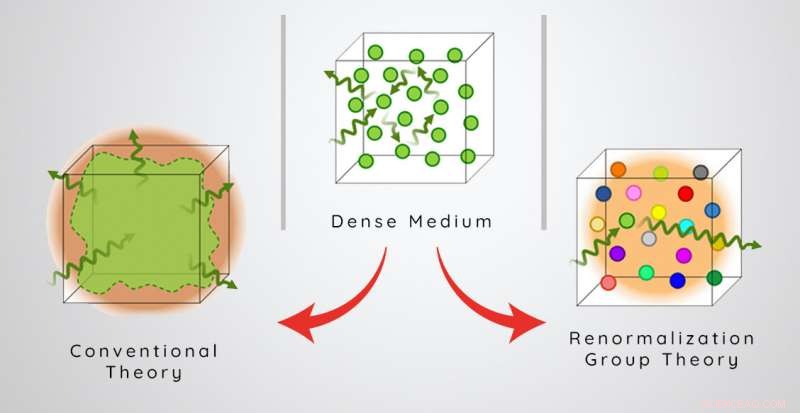
Schematische illustratie van de optische respons van een dicht atomair medium gezien door traditionele theorieën versus de RG-theorie. Krediet:ICFO
Pink Floyd's Dark Side of the Moon-cover, uitgeroepen tot het beste klassieke rockalbum aller tijden, bedoeld om het prisma en de verspreiding van licht in een regenboog af te beelden als een bepaalde metaforische symboliek en een lichtshow die nooit werd gevierd. Echter, ze waren zich er echt niet van bewust dat dit beeld door velen zou worden gebruikt om het concept van de brekingsindex te illustreren en hoe licht van snelheid en richting verandert wanneer het een ander medium tegenkomt.
Hoewel de tekening conceptueel niet juist was, het bracht de boodschap over dat licht van snelheid verandert wanneer het naar een ander medium gaat, en dat de verschillende snelheden van verschillende kleuren ervoor zorgen dat wit licht zich verspreidt in de verschillende componenten. Deze snelheidsverandering is gerelateerd aan de brekingsindex, een eenheidsloos getal dat de verhouding weergeeft tussen de lichtsnelheid in vacuüm en de lichtsnelheid in een medium.
In het algemeen, alle materialen met positieve brekingsindices hebben waarden dicht bij 1 voor zichtbaar licht. Of dit gewoon toeval is of een diepere fysica weerspiegelt, is nooit verklaard.
Nutsvoorzieningen, in een recente studie gepubliceerd in Fysieke beoordeling X en benadrukt door de redactie, ICFO-onderzoekers Francesco Andreoli en ICREA Prof. bij ICFO Darrick Chang, in samenwerking met onderzoekers van Princeton University, Universiteit van Chicago en Institut d'Optique, hebben onderzocht en uitgelegd waarom de brekingsindex van een verdund atomair gas slechts een maximale waarde van 1,7 kan bereiken, ongeacht hoe hoog de dichtheid van atomen wordt.
Dit resultaat is in tegenstelling tot conventionele leerboektheorieën, die voorspellen dat hoe meer materiaal er is, hoe groter de optische respons en de brekingsindex kunnen zijn. De uitdaging om het probleem goed te begrijpen, heeft te maken met meervoudige verstrooiing van licht - alle complexe paden die licht in een medium kan afleggen - en de resulterende interferentie. Dit kan ertoe leiden dat elk individueel atoom een lokale lichtintensiteit ziet die heel anders is dan de intensiteit die wordt ingestuurd, en die varieert afhankelijk van de geometrie van de atomen eromheen. In plaats van zich bezig te houden met de complexe microscopische details van deze granulariteit, leerboeken gaan er vaak op de een of andere manier van uit dat deze granulariteit en de effecten ervan op licht kunnen worden afgevlakt.
In tegenstelling tot, de teams maken gebruik van een theorie, sterke stoornis renormalisatiegroep (RG) genoemd, waardoor ze op een eenvoudige manier granulariteit en meerdere verstrooiingseffecten kunnen vastleggen. Deze theorie laat zien dat de optische respons van een bepaald atoom onevenredig wordt beïnvloed door zijn enkele naaste buur vanwege near-field-interacties, dat is de reden waarom typische afvlakkingstheorieën falen. Het fysieke effect van de nabije-veldinteracties is het produceren van een inhomogene verbreding van atomaire resonantiefrequenties, waar de hoeveelheid verbreding groeit met de dichtheid. Dus, hoe hoog de fysieke dichtheid van atomen ook is, inkomend licht van elke frequentie zal slechts ongeveer 1 bijna-resonant atoom per kubieke golflengte zien om efficiënt te verstrooien, die de brekingsindex beperkt tot zijn maximale waarde van 1,7.
Breder, deze studie suggereert dat de RG-theorie een nieuw veelzijdig hulpmiddel zou kunnen zijn om het uitdagende probleem van meervoudige verstrooiing van licht in bijna-resonante ongeordende media te begrijpen, inclusief in de niet-lineaire en kwantumregimes. Het toont ook de belofte om te proberen de limieten van de brekingsindex van echte materialen te begrijpen, bottom-up beginnen met de individuele atomen waaruit ze zijn samengesteld.
 Calcium-oxalaat
Calcium-oxalaat Wat voor soort reactie komt er met waterstofchloride en Alka Seltzer?
Wat voor soort reactie komt er met waterstofchloride en Alka Seltzer?  Waarom krimpt een ei in verschillende oplossingen?
Waarom krimpt een ei in verschillende oplossingen?
Een ei krimpt als het in een oplossing wordt geplaatst met een hogere opgeloste concentratie dan in het ei. In een oplossing wordt de stof die het oplossen doet een oplosmiddel genoemd. De stof die
 Hoe massa in gram van een molecuul berekenen
Hoe massa in gram van een molecuul berekenen  Het water en het zweet opzuigen - een nieuw superdroogmiddel
Het water en het zweet opzuigen - een nieuw superdroogmiddel
 5 dingen die u moet weten over het nieuwe VN-rapport over klimaatverandering
5 dingen die u moet weten over het nieuwe VN-rapport over klimaatverandering Duurzame Lego - plastic uit planten lost een vervuilingscrisis niet op
Duurzame Lego - plastic uit planten lost een vervuilingscrisis niet op Zesvoudige sprong in poolijsverlies verhoogt wereldwijde oceanen
Zesvoudige sprong in poolijsverlies verhoogt wereldwijde oceanen Cryptozoology: The Pseudo-Science of Mythical Creatures
Cryptozoology: The Pseudo-Science of Mythical Creatures  Catalogus van aardbevingen in Noord-Texas bevestigt aanhoudende effecten van afvalwaterafvoer
Catalogus van aardbevingen in Noord-Texas bevestigt aanhoudende effecten van afvalwaterafvoer
Hoofdlijnen
- Osmose & celstructuur
- Bloem trekt insecten aan door zich voor te doen als paddenstoel
- Het publiek is minder bang voor haaien als ze hun gedrag begrijpen
- Inleiding tot hoe gigantische virussen werken
- Nieuwe procedure voor snellere detectie van milieueffecten van zalmkwekerijen
- Hoe is zuurstof belangrijk voor de afgifte van energie in de celademhaling?
- Onderzoekers rapporteren bevindingen over de controle van celdeling
- Er wordt een verrassende nieuwe vlindervis beschreven uit de Filippijnse schemerzone en tentoonstelling
- Een niet-verslavende opioïde pijnstiller zonder bijwerkingen
- Wetenschappers gebruiken bacteriën om levende vloeibare kristallen te maken

- Hoe hebben genetische parasieten de natuurlijke selectie miljarden jaren lang overwonnen?
- Microscopie verplaatsen voorbij de resolutielimiet

- Waarom is er überhaupt materie in het universum? Nieuwe studie werpt licht

- Thermische spinstromen bevestigd in zowel ruimte als tijd

 Nieuwe tool visualiseert de voordelen van de natuur wereldwijd
Nieuwe tool visualiseert de voordelen van de natuur wereldwijd Nieuw onderzoek onthult de geheimen van fotosynthese die zouden kunnen helpen bij de ontwikkeling van computertechnologie
Nieuw onderzoek onthult de geheimen van fotosynthese die zouden kunnen helpen bij de ontwikkeling van computertechnologie Door de gebruiker aanpasbare computerengine voor taken op het gebied van kunstmatige intelligentie
Door de gebruiker aanpasbare computerengine voor taken op het gebied van kunstmatige intelligentie Onderzoeker helpt zeldzame, iconische bomen
Onderzoeker helpt zeldzame, iconische bomen In zonsverduisteringen pad van totaliteit, kamers gaan voor $ 1, 000 en verkopers verkopen elke snuisterij onder de zon
In zonsverduisteringen pad van totaliteit, kamers gaan voor $ 1, 000 en verkopers verkopen elke snuisterij onder de zon Zes wetenschappelijke tijdschriften hekelen de milieuhervorming van Trump
Zes wetenschappelijke tijdschriften hekelen de milieuhervorming van Trump Een gepatenteerde oplossing voor het verlichten van droge mond en de ontwikkeling van voedingsproducten
Een gepatenteerde oplossing voor het verlichten van droge mond en de ontwikkeling van voedingsproducten Als eenhoorns echt waren,
Als eenhoorns echt waren,
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

