
Wetenschap
Optimalisatie van structuren binnen complexe arrangementen van bellen

Krediet:CC0 Publiek Domein
Terwijl structuren die schuimachtige arrangementen van bellen nabootsen, lichtgewicht en goedkoop zijn om te bouwen, ze zijn ook opmerkelijk stabiel. De bubbels die het iconische Beijing Aquatics Centre bedekken, bijvoorbeeld, hebben allemaal hetzelfde volume, maar zijn zo gerangschikt dat het totale oppervlak van de constructie tot een minimum wordt beperkt, waardoor de constructie van het gebouw wordt geoptimaliseerd. De wiskunde die aan dit gedrag ten grondslag ligt, wordt nu goed begrepen, maar als de oppervlakten van de bellen niet gelijk zijn, de situatie wordt ingewikkelder. uiteindelijk, dit maakt het moeilijker om algemene uitspraken te doen over hoe de totale oppervlakte of, in 2D, rand lengte, of 'omtrek', kan worden geminimaliseerd om de structurele stabiliteit te optimaliseren.
In nieuw onderzoek gepubliceerd in Het European Physical Journal E , Francis Headley en Simon Cox van de Aberystwyth University in het Verenigd Koninkrijk onderzoeken hoe verschillende aantallen 2-D-bubbels van twee verschillende gebieden kunnen worden gerangschikt in cirkelvormige schijven, op manieren die hun omtrek minimaliseren.
Met behulp van computersimulaties van maximaal tien bellen, het duo onderzocht hoe de vormen van de bubbels geoptimaliseerd konden worden, terwijl ze de wiskundige wetten voor bellenvorming gehoorzamen. Hun werk zou de weg kunnen banen voor nieuwe ontwerpen van complexe schuimachtige structuren die zowel sterker als goedkoper zijn dan eerdere ontwerpen. Het zou ook nieuwe inzichten kunnen verschaffen in de algemene natuurkundige wetten die de optimale lay-out van bellen met verschillende gebieden bepalen. Om tot deze conclusies te komen, Headley en Cox merkten op hoe de complexiteit snel toeneemt voor grotere aantallen totale bellen; terwijl vijf bubbels op 20 verschillende manieren kunnen worden gerangschikt, in totaal 314, 748 structuren zijn mogelijk voor tien bellen.
Headley en Cox berekenden hun optimale bellenrangschikking met behulp van geavanceerde software om de laagste omtrekrangschikking van bellen voor elke oppervlakteverhouding te vinden. Voor elke hoeveelheid bubbels, ze hebben uiteindelijk vastgesteld dat het aantal structuren met de kleinste omtrek voor een bepaald bereik van oppervlakteverhoudingen toenam naarmate het aantal bellen toenam, en vandaar dat het bereik van oppervlakteverhoudingen dat een bepaalde bellenstructuur met de kleinste omtrek oplevert, smaller werd.
 Nieuwe sneltest detecteert kwaliteit en authenticiteit van olijfolie
Nieuwe sneltest detecteert kwaliteit en authenticiteit van olijfolie Hoe te bepalen of zouten zuren of basisch zijn
Hoe te bepalen of zouten zuren of basisch zijn Proces voor het maken van plastic flessen
Proces voor het maken van plastic flessen Ontdekking versterkt de theorie dat het leven op aarde is ontstaan uit een RNA-DNA-mix
Ontdekking versterkt de theorie dat het leven op aarde is ontstaan uit een RNA-DNA-mix Van overvloedige koolwaterstoffen tot zeldzame spinvloeistoffen
Van overvloedige koolwaterstoffen tot zeldzame spinvloeistoffen
 Klimaatverandering kan oceanen van vriend in vijand veranderen, VN-rapport waarschuwt
Klimaatverandering kan oceanen van vriend in vijand veranderen, VN-rapport waarschuwt Onderzoeker onderzoekt mogelijke link tussen klimaatverandering en watertoxiciteit
Onderzoeker onderzoekt mogelijke link tussen klimaatverandering en watertoxiciteit Afnemende instroom in stroomgebieden:een ramp met de watervoorziening in de maak?
Afnemende instroom in stroomgebieden:een ramp met de watervoorziening in de maak? Het mobiliseren van wereldwijd kapitaal in de nasleep van een ramp is essentieel voor economisch herstel
Het mobiliseren van wereldwijd kapitaal in de nasleep van een ramp is essentieel voor economisch herstel Fotosynthese in pijnbomen
Fotosynthese in pijnbomen
Hoofdlijnen
- Wetenschappers maken cellen die de tastzin mogelijk maken
- Vermont ziet hedendaags record voor reproductie van Amerikaanse zeearenden
- Episch taaie baobabbomen sterven af in Afrika
- Grootte doet er niet toe - althans voor hamerhaaien en zwemprestaties
- Hoe zijn fotosynthese en cellulaire ademhaling gerelateerd
- De handel in neushoornhoorn legaliseren - reken niet blindelings aan
- Wat is het voordeel van het gebruik van vlekken om naar cellen te kijken?
- Wetenschappers hebben het allereerste roestpathogeen gen geïsoleerd dat tarweplanten detecteren om resistentie in te schakelen
- Knoflook kan chronische infecties bestrijden
- Vierkante inches converteren naar kubieke voet

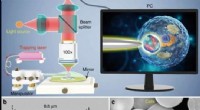
- Kleiner door cellen zien:een natuurlijke eencellige biomagnifier voor beeldvorming onder de golflengte
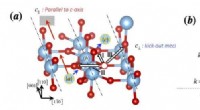
- Nieuwe kwantumbenadering helpt bij het oplossen van een oud probleem in de materiaalkunde
- Kunnen we naar de kat van Schrödinger gluren zonder hem te storen?

- Wetenschap onthult verbeteringen in Romeinse bouwtechnieken

 Video:vijf dingen die je misschien niet wilt combineren met anticonceptie
Video:vijf dingen die je misschien niet wilt combineren met anticonceptie Aanwijzingen voor de aangeboren resistentie tegen geneesmiddelen van een cacaofermenterende ziekteverwekker
Aanwijzingen voor de aangeboren resistentie tegen geneesmiddelen van een cacaofermenterende ziekteverwekker Onderzoeksteam ontwikkelt materiaal om olie en water te scheiden voor milieusanering en afvalwaterzuivering
Onderzoeksteam ontwikkelt materiaal om olie en water te scheiden voor milieusanering en afvalwaterzuivering Het stereotype van een racistische politieagent kan een self-fulfilling prophecy worden
Het stereotype van een racistische politieagent kan een self-fulfilling prophecy worden Kleine prehistorische hagedis werpt licht op de evolutie van reptielen
Kleine prehistorische hagedis werpt licht op de evolutie van reptielen Hoe reproduceren algen zich?
Hoe reproduceren algen zich?  Groen en sociaal beleid helpt bedrijven de COVID-19-crash te doorstaan
Groen en sociaal beleid helpt bedrijven de COVID-19-crash te doorstaan Top 5 manieren waarop NASA het milieu helpt
Top 5 manieren waarop NASA het milieu helpt
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

