
Wetenschap
Nieuwe klasse van isolerende kristallen herbergt gekwantiseerde elektrische multipoolmomenten
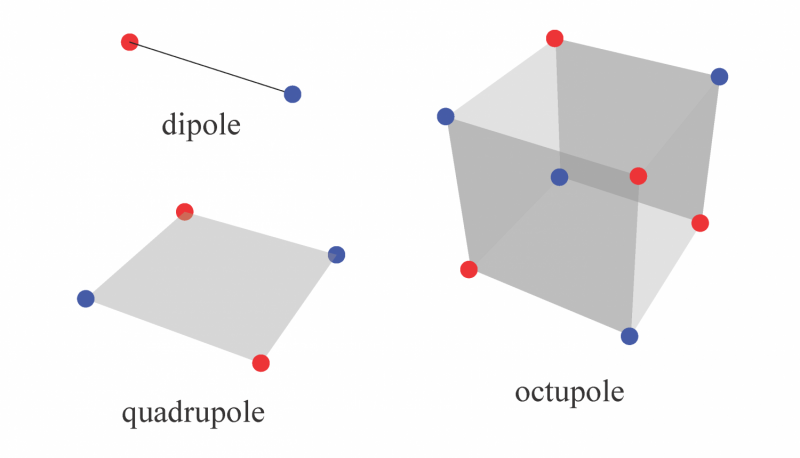
In deze figuur is het elektrische dipoolmoment wordt weergegeven door een positieve lading (rode stip) en een negatieve lading (blauwe stip) die ruimtelijk gescheiden zijn. de quadrupool, bestaande uit twee tegengestelde dipoolmomenten, is inherent tweedimensionaal, en de achtpool, bestaande uit twee tegenover elkaar liggende quadrupolen, is inherent driedimensionaal. Terwijl materialen met gekwantiseerde dipoolmomenten eerder bekend waren, isolerende kristallen met gekwantiseerde quadrupool- en octupoolmomenten zijn topologische fasen die tot nu toe niet zijn ontdekt. Krediet:Wladimir Balcazar, Afdeling Natuurkunde en Instituut voor Theorie van de Gecondenseerde Materie, Universiteit van Illinois in Urbana-Champaign.
Onderzoekers van de Universiteit van Illinois in Urbana-Champaign en Princeton University hebben theoretisch een nieuwe klasse van isolerende fasen van materie in kristallijne materialen voorspeld, vastgesteld waar ze in de natuur te vinden zijn, en veralgemeende daarbij de fundamentele kwantumtheorie van Berry-fasen in vaste-stofsystemen. Bovendien, deze isolatoren genereren elektrische quadrupool- of octupoolmomenten - die ruwweg kunnen worden beschouwd als zeer specifieke elektrische velden - die worden gekwantiseerd. Gekwantiseerde waarnemingen zijn een gouden standaard in onderzoek naar gecondenseerde materie, omdat experimentele resultaten die deze waarnemingen meten moeten, in principe, exact overeenkomen met theoretische voorspellingen, zodat er geen twijfel mogelijk is, zelfs in zeer complexe systemen.
Het onderzoek, dat is de gecombineerde inspanning van afgestudeerde student Wladimir Benalcazar en universitair hoofddocent natuurkunde Taylor Hughes van het Institute for Condensed Matter Theory aan de U. of I., en hoogleraar natuurkunde B. Andrei Bernevig van Princeton, wordt gepubliceerd op 7 juli 2017 nummer van het tijdschrift Wetenschap .
Het werk van het team begon met het identificeren van een vierpolige isolator, maar het werd al snel duidelijk dat er diepere implicaties waren.
Benalcazar legt uit, "Een van de nieuwe modellen die het werk presenteert, heeft een gekwantiseerd elektrisch quadrupoolmoment. Het is een isolator in tegenstelling tot alle eerder bekende topologische isolatoren. Het heeft geen gapless, laagenergetische oppervlaktetoestanden - het kenmerk van dergelijke systemen - wat misschien de reden is waarom deze systemen al zo lang geen ontdekking hebben gedaan."
"Maar opmerkelijk, " hij gaat door, "ook al zijn de oppervlakken van de vierpolige isolator gespleten, ze zijn niet onbelangrijk. In feite, ze vormen een lager-dimensionale topologische isolatorfase! Onze berekeningen kunnen voorspellen wanneer een systeem dergelijke grenstopologische isolatoren zal herbergen - of het nu aan de oppervlakte, scharnieren, of hoeken. Verrassend genoeg, deze eigenschap in zijn meest elementaire vorm is gerelateerd aan de hogere elektrische multipoolmomenten."
Revolutionair werk in de jaren 1990 en 2000 door Vanderbilt, Koning-Smith, Resta, Martin, Ortiz, Marzari, en Souza, maakte het mogelijk om het dipoolmoment van een kristal te definiëren door een bepaalde toepassing van de Berry-fase - een wiskundige grootheid die de evolutie van elektronengolffuncties in de impulsruimte van het rooster kenmerkt. Dat werk betekende een enorme vooruitgang in ons begrip van topologische elektromagnetische verschijnselen in kristallijne materialen. Het leverde een verband tussen een fysieke grootheid (dipoolmoment) en een topologische (Berry-fase). Volgens Hughes en Bernevig, het huidige onderzoek begon als een poging om de dipoolmomenttheorie te generaliseren naar hogere multipoolmomenten.
Hughes vertelt, "In de vroegste stadia Andrei en ik bespraken het idee om het werk aan kristallijne dipoolmomenten uit te breiden tot quadrupoolmomenten. Maar het blijkt, terwijl de vraag eens gesteld enigszins voor de hand leek, de wiskundige oplossing was dat niet. Het berekenen van multipoolmomenten in een kwantummechanisch systeem van elektronen is een uitdaging omdat het elektron, een kwantummechanisch deeltje, is een golf, niet zomaar een deeltje, en de locatie in de ruimte is onzeker. Terwijl het dipoolmoment kan worden bereikt door alleen de elektronenverplaatsing te meten, een vectorhoeveelheid, de quadrupoolmomenten zijn lastiger."
Dit behandelen, de wetenschappers moesten een nieuw theoretisch kader bedenken. In aanvulling, ze moesten modellen bouwen met de juiste eigenschappen waarmee ze hun nieuwe analytische techniek konden benchmarken. Maar eigenlijk, dingen gebeurden in precies de tegenovergestelde volgorde:Hughes en Bernevig crediteren Benalcazar met het vinden van het juiste model, een generalisatie van een dipoolisolator met een gekwantiseerd dipoolmoment. Vanaf daar, het kostte een heel jaar om het volledige theoretische kader op te bouwen.
Bestaande wiskundige hulpmiddelen - de vaste-stof Berry-fasen - konden de positie van het elektron slechts in één richting tegelijk oplossen. Maar voor het quadrupoolmoment, het team moest zijn positie in twee dimensies tegelijk bepalen. De complicatie komt voort uit de
onzekerheidsprincipe van Heisenberg, waarin meestal staat dat je niet tegelijkertijd zowel de positie als het momentum van een elektron kunt meten. Echter, in de nieuwe vierpolige isolatoren, een ander onzekerheidsprincipe aan het werk is, het voorkomen van gelijktijdige meting van de positie van het elektron in zowel de X- als de Y-richting. Daarom, de auteurs konden de elektronenlocaties niet ruimtelijk oplossen met behulp van bestaande theoretische hulpmiddelen.
"We kunnen het in één richting vastpinnen, maar niet de andere, "Benalcazar herinnert zich. "Om beide richtingen tegelijkertijd te krijgen, creëerden we een nieuw analytisch paradigma, in wezen door het quadrupoolmoment te scheiden in een paar dipolen."
Hughes voegt eraan toe, "Aanvankelijk, we voerden elke test uit die we wisten uit te voeren op de modellen die we voorstelden en kwamen steeds met niets. Het probleem is, als twee dipolen op elkaar liggen, ze heffen elkaar op. Om de quadrupool te zien, heb je enige ruimtelijke resolutie nodig om te bepalen of de dipolen echt gescheiden zijn. Uiteindelijk bleek, we moesten de Berry-fasen een laag dieper bekijken, wiskundig gesproken."
Het vinden van een manier om die tweede dimensie ruimtelijk op te lossen, betekent een belangrijke theoretische doorbraak. De auteurs bedachten een nieuw paradigma voor het berekenen van de locatie van elektronen dat een uitbreiding is van de Berry-faseformulering. Eerst, ze gebruiken een conventionele techniek om de elektronengolf theoretisch op te splitsen in twee ladingswolken, gescheiden in de ruimte. Vervolgens laten ze zien dat elke wolk een dipoolmoment heeft. Deze tweetraps, geneste procedure kan twee ruimtelijk gescheiden, tegengestelde dipolen - een quadrupool.
Bernevig merkt op, "De topologische isolatoren waaraan we het afgelopen decennium gewend zijn geraakt, worden allemaal in wezen beschreven door een wiskundige procedure die de Berry-fase van sommige elektronische toestanden wordt genoemd. De Berry-fase van het binnenste van een monster, in werkelijkheid, kent de rand van een systeem - het kan u vertellen wat er interessant is aan de rand.
Om een stap verder te gaan en op te lossen wat potentieel opmerkelijk is aan de hoek van een systeem of monster, je moet nemen, in werkelijkheid, een Berry-fase van een Berry-fase. Dit leidt tot de formulering van een nieuwe topologische grootheid die het gekwantiseerde quadrupoolmoment beschrijft."
In het laatste decennium, de classificatie van topologische fasen van materie is aanzienlijk ontwikkeld. aanzienlijk, dit nieuwe werk toont de nog onontgonnen rijkdom van het veld. Het voorspelt een geheel nieuwe klasse van fasen en verschaft het model en de theoretische middelen om het bestaan ervan te testen. Misschien wel een van de meest opwindende aspecten op het gebied van topologische isolatoren is hun experimentele relevantie. In het tijdschriftartikel, het team stelt drie mogelijke experimentele opstellingen voor om hun voorspelling te valideren.
Hughes erkent dat een kwantumsimulatie - een experimentele techniek die, bijvoorbeeld, maakt gebruik van fijn afgestemde lasers en ultrakoude atomen om de eigenschappen van echte materialen te repliceren en te onderzoeken - zou het meest direct toegankelijk zijn.
"Het is spannend dat met behulp van de huidige experimentele technologie, ons model is direct te bekijken, Hughes bevestigt. "We hopen dat wij of iemand anders uiteindelijk een elektronische, solid-state materiaal met dit soort eigenschappen. Maar dat is een uitdaging, we hebben nog geen chemische formule."
De auteurs geven aan dat de voorwaarden om dit effect te krijgen vrij algemeen zijn, en als zodanig zijn er veel potentiële kandidaten in veel materiaalklassen.
"Of het besef zou op een dag uit het linkerveld kunnen komen, van een ander uiterst ingenieus implementatie-idee dat iemand zou kunnen bedenken, ’, grapt Bernevig.
Benzalcazar is ervan overtuigd dat "dit nieuwe begrip een hele verzameling materialen kan openen die deze hiërarchische classificatie hebben."
Dit is fundamenteel onderzoek, en eventuele toepassingen zijn nog een verre kwestie van vermoeden. Omdat gekwantiseerde waarneembare objecten uiterst nauwkeurige metingen mogelijk maken, het is denkbaar dat de nieuwe elektrische eigenschappen van deze nieuwe fase van materie nuttig zullen zijn in de metrologie, elektronische technologieën, of bij het ontwerpen van materialen met voorgeschreven bulk-/oppervlakte-/rand-/hoekeigenschappen.
De auteurs zijn het erover eens, dit werk opent veel mogelijkheden voor nieuwe topologische systemen die voorheen verborgen waren - verborgen in de geneste structuur van de Berry-fase-wiskunde. Deze verborgen topologische fasen hebben een scherpe verbinding met echte fysieke waarneembaarheden - en er kunnen andere fysieke verschijnselen in deze materialen zijn die interessant zijn om te onderzoeken.
 Wat wordt overgebracht tussen een geconjugeerd zuur basepaar?
Wat wordt overgebracht tussen een geconjugeerd zuur basepaar?  Nieuwe strategie ontworpen voor duurzame productie van benzylamines uit lignine
Nieuwe strategie ontworpen voor duurzame productie van benzylamines uit lignine Gram omzetten in moleculen
Gram omzetten in moleculen  Wetenschappers leggen de eerste cryo-EM-beelden vast van cellulair doelwit voor diabetes type 2 in actie
Wetenschappers leggen de eerste cryo-EM-beelden vast van cellulair doelwit voor diabetes type 2 in actie Algoritme identificeert optimale paren voor het samenstellen van metaal-organische raamwerken
Algoritme identificeert optimale paren voor het samenstellen van metaal-organische raamwerken
 Drempel voor gevaarlijke klimaatopwarming zal waarschijnlijk worden overschreden tussen 2027-2042
Drempel voor gevaarlijke klimaatopwarming zal waarschijnlijk worden overschreden tussen 2027-2042 De ervaring van Japan met aardbevingen kan ons helpen om te leren leven met overstromingen
De ervaring van Japan met aardbevingen kan ons helpen om te leren leven met overstromingen Verontreinigende stoffen veranderen het water in de buurt van Ieodo Island snel
Verontreinigende stoffen veranderen het water in de buurt van Ieodo Island snel De Green New Deal verandert al de voorwaarden van het debat over klimaatactie
De Green New Deal verandert al de voorwaarden van het debat over klimaatactie NASA onderzoekt structurele veranderingen in de tropische storm Gonzalos
NASA onderzoekt structurele veranderingen in de tropische storm Gonzalos
Hoofdlijnen
- Mariene wetenschappers ontdekken kleptopredatie - een nieuwe manier om prooien te vangen
- Wetenschappers onderzoeken hoe olie de kleinste organismen in Antarctische wateren beïnvloedt
- Zijn kleine populieren de toekomst van biobrandstoffen? Studies zeggen ja
- 10 misvattingen over de griep
- Geslachtsrollen in de oudheid
- Wetenschapsprojecten over Dominant en Recessieve Genen
- Het bewijs zit in de voetafdruk:mensen kwamen eerder naar Amerika dan gedacht
- Overeenkomsten tussen verbranding en cellulaire ademhaling
- Hoe vergif Sumac te behandelen?
- Hoe krijg ik een deeltjesdetector in een vliegtuig?

- Wetenschappers doen eerste waarnemingen van hoe een meteoorachtige schok silica in glas verandert

- Wat zijn de verschillende klassen hefbomen?

- In atoompropellers, kwantumverschijnselen kunnen alledaagse natuurkunde nabootsen

- Uitgerekte fotonen herstellen verloren interferentie

 Klimaatverandering duwt Nieuw-Zeeland de warmste geregistreerde winter in
Klimaatverandering duwt Nieuw-Zeeland de warmste geregistreerde winter in Formaldehyde is overal,
Formaldehyde is overal,  Onpartijdigheid van de media over klimaatverandering is ethisch misleidend en ronduit gevaarlijk
Onpartijdigheid van de media over klimaatverandering is ethisch misleidend en ronduit gevaarlijk De natuur kan zichzelf genezen na een olieramp, het heeft alleen een beetje hulp nodig
De natuur kan zichzelf genezen na een olieramp, het heeft alleen een beetje hulp nodig Verschillende populaire apps, waaronder Yelp, sturen automatisch gegevens naar Facebook, waakhondgroep zegt:
Verschillende populaire apps, waaronder Yelp, sturen automatisch gegevens naar Facebook, waakhondgroep zegt: Nanodeeltjes wegen op de attogramschaal
Nanodeeltjes wegen op de attogramschaal Op weg naar een slimme pleister die automatisch insuline toedient wanneer dat nodig is
Op weg naar een slimme pleister die automatisch insuline toedient wanneer dat nodig is Silicium microtrechters verhogen de efficiëntie van zonnecellen
Silicium microtrechters verhogen de efficiëntie van zonnecellen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

