
Wetenschap
Eén in 1000 jaar? Oude overstromingskansen houden geen steek meer
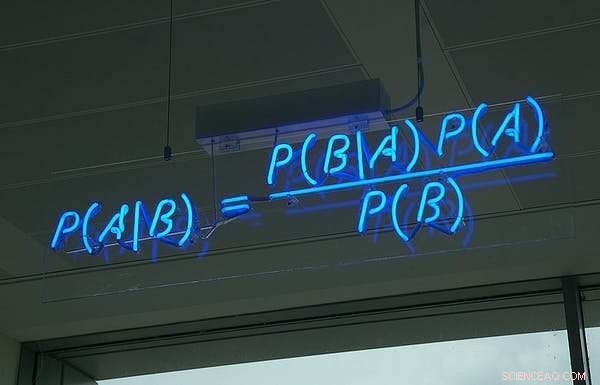
De stelling van Bayes, in neon, in het kantoor van het Britse softwarebedrijf HP Autonony. Krediet:Wikimedia Commons, CC BY
De catastrofale overstromingen aan de oostkust van Australië zijn door de premier van NSW beschreven als een "een op de 1000-jarige gebeurtenis, een term die veel verwarring heeft veroorzaakt.
Lange uitleg dat deze termen niet hetzelfde zijn als "die 1000 jaar na elkaar voorkomen" of "eens in de 1000 jaar" hebben de verwarring alleen maar vergroot.
De eenvoudigste verklaring is dat de werkelijke betekenis van "één op 1000 jaar" is "een kans van 0,1 procent hebben in een bepaald jaar" (1 op 1000), wat de vraag oproept:waarom zeggen mensen dat niet gewoon?
De belangrijkste reden is dat deze termen dateren uit een tijd waarin de meeste mensen niet in termen van waarschijnlijkheden dachten, en zelfs degenen die dat wel deden, waren in de war over hoe ze werkten. Tegenwoordig hebben we voortdurend interactie met waarschijnlijkheden.
De dagelijkse weersvoorspelling omvat een procentuele kans op regen, en voorspellingen op langere termijn geven de kans op meer of minder dan gemiddelde regenval volgens de El Nino- en La Nina-cycli.
Financiële markten wedden op de kansen of rentebewegingen. Statistieken en kansrekening worden op school aan kinderen onderwezen.
Maar dit is een vrij recente ontwikkeling.
Tot de 17e eeuw waren zelfs de meest elementaire concepten van de kansrekening onbekend. Mensen dachten dat lot en fortuin in wezen onkenbaar waren. Zelfs gokkers begrepen de kansen niet.
De geboorte van waarschijnlijkheid
Het was inderdaad een verzoek van een gokkervriend rond 1654 die de Franse filosoof en wiskundige Blaise Pascal motiveerde om samen met collega-wiskundige Pierre de Fermat de basisconcepten van waarschijnlijkheid te ontwikkelen.
(Pascal gebruikte het idee ook om "Pascal's weddenschap" te ontwikkelen om het nut van het geloven in God aan te tonen. Het idee is dat als God bestaat, gelovigen zullen worden beloond met eeuwige gelukzaligheid. Zo niet, dan zullen ze afzien van een beperkt aantal aardse genoegens terwijl Het maakt niet uit hoe klein de kans is dat God bestaat, het voordeel van geloven in God blijkt oneindig te zijn, terwijl de kosten eindig zijn.)
Het begrip ontwikkelde zich langzaam. Het was pas in het midden van de 18e eeuw dat de Engelse predikant Thomas Bayes de belangrijkste ontwikkeling van het veld werd gecrediteerd.
De tool nagelaten door Bayes
In zijn moderne interpretatie geeft de stelling van Bayes ons de middelen om onze kijk op de waarschijnlijkheid van een gebeurtenis te herzien in het licht van bewijs over wat er zojuist is gebeurd.
Of er zojuist iets is gebeurd of niet, wordt expliciet meegenomen in de herberekening, samen met bijgewerkte beoordelingen van de waarschijnlijkheid dat dat ertoe doet.
Tot Bayes werden de meeste kansen berekend alsof ze onveranderlijk waren, zoals de kans om "kop" te krijgen bij het opgooien van een munt. Die kansen zouden met goed gevolg kunnen worden omschreven als 'één op de 1000 jaar' of 'gemiddeld elke seconde opgooien'.
Maar de kans op een ernstige overstroming verandert in de loop van de tijd naarmate de relatie tussen de componenten waaruit het weersysteem bestaat, verandert. Of er een overstroming heeft plaatsgevonden geeft ons bewijs over die verandering.
Dit maakt het niet langer nuttig om naar een ernstige overstroming te verwijzen als "één in x jaar"-gebeurtenis.
Het is lang voorbij de tijd dat we de terminologie van eens in de zoveel jaren veranderden, maar naar wat? Het antwoord lijkt eenvoudig, hoewel de details lastig zullen zijn.
Ten eerste moeten we de oude maatregelen omzetten in ernstschalen, vergelijkbaar met die voor cyclonen en aardbevingen, maar specifiek voor elk stroomgebied.
Als dat is gebeurd, kan de waarschijnlijkheid van een gebeurtenis van een bepaalde ernst worden geschat op basis van historische ervaring en worden bijgewerkt in het licht van nieuw bewijs.
Hoe zou dit van toepassing zijn in het geval van een gebeurtenis als de overstroming van Lismore?
De aanvankelijke beschrijving "één op de 1000 jaar" betekent dat een dergelijke gebeurtenis uiterst onwaarschijnlijk zou zijn als de oude relatie stand zou houden.
Met behulp van de stelling van Bayes zouden we de eerste kans op 1000 bijwerken op basis van bijgewerkte informatie over de kans dat de onderliggende relaties veranderen, waardoor elk jaar nieuwe kansen ontstaan.
Dit is hoe machine learning werkt en hoe medische en verzekeringskansen worden bijgewerkt. Helaas zullen de herziene kansen vrijwel zeker meer dan één op 1.000 bedragen.
 Hoe veranderen neonlichten van kleur?
Hoe veranderen neonlichten van kleur?  Nieuw, op waterbasis, recyclebare membraanfilters alle soorten nanodeeltjes
Nieuw, op waterbasis, recyclebare membraanfilters alle soorten nanodeeltjes Stikstof verminderen met boor en bier
Stikstof verminderen met boor en bier Wetenschappers herleven oude eiwitten om aanwijzingen te geven over moleculaire innovatie
Wetenschappers herleven oude eiwitten om aanwijzingen te geven over moleculaire innovatie Onderzoekers optimaliseren methoden om bruikbare verbindingen uit biomassa te produceren
Onderzoekers optimaliseren methoden om bruikbare verbindingen uit biomassa te produceren
Hoofdlijnen
- Routes uit isolatie voor Yellowstone grizzlyberen
- Wat is de ergste uitsterving in de geschiedenis van de aarde?
- Cellulaire ademhaling in planten
- Tumorsuppressorgenen: wat is het?
- Hoe een 3D-model voor celbiologieprojecten te bouwen Mitochondria & Chloroplast
- Wetenschappers ontdekken nieuw soort synaps in kleine haartjes van neuronen
- Studie belicht de instandhoudingsbehoeften van recent ontdekte vissoorten in Southwest Virginia
- Oceaanmonumenten worden geconfronteerd met mogelijk verlies van bescherming
- Wat is een eencellige eukaryoot?
- Genderbias op de werkvloer begint bij communicatie tijdens werving

- Welk gebruik maken tieners van YouTube?

- Coronavirus:Strategische Nationale Voorraad was klaar, maar niet hiervoor

- Nieuwe kaarttechniek kan helpen extreme armoede te bestrijden
- Student onthult het gezicht van vrouwelijke druïde uit de ijzertijd

 Mars-missies vanuit China en de VAE zullen in een baan om de aarde gaan - dit is wat ze konden ontdekken
Mars-missies vanuit China en de VAE zullen in een baan om de aarde gaan - dit is wat ze konden ontdekken Onderzoek laat zien hoe contact met rechtshandhaving, ook voor familieleden, vermindert politieke participatie
Onderzoek laat zien hoe contact met rechtshandhaving, ook voor familieleden, vermindert politieke participatie Topologische supergeleidende fase beschermd door 1-D lokale magnetische symmetrieën
Topologische supergeleidende fase beschermd door 1-D lokale magnetische symmetrieën Een laser op nanoschaal gemaakt van goud en zinkoxide
Een laser op nanoschaal gemaakt van goud en zinkoxide Canadezen hebben meer seks tijdens de pandemie, tenzij ze bij hun partners wonen
Canadezen hebben meer seks tijdens de pandemie, tenzij ze bij hun partners wonen Nieuwe moleculaire eigenschappen kunnen efficiëntere zonne- en opto-elektronische apparaten betekenen
Nieuwe moleculaire eigenschappen kunnen efficiëntere zonne- en opto-elektronische apparaten betekenen Stimuleringsbetalingen zorgden voor meer uitgaven onder bevolkingsgroepen met een laag inkomen in de VS
Stimuleringsbetalingen zorgden voor meer uitgaven onder bevolkingsgroepen met een laag inkomen in de VS Wat is het voordeel van het gebruik van vlekken om naar cellen te kijken?
Wat is het voordeel van het gebruik van vlekken om naar cellen te kijken?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

