
Wetenschap
Topologische supergeleidende fase beschermd door 1-D lokale magnetische symmetrieën

Krediet:CC0 Publiek Domein
Topologische supergeleiders (TSC's) zijn een nieuw soort topologische kwantumtoestanden met een volledig supergeleidende bandstructuur met gaten in de bulk, maar ze ondersteunen gapless excitaties genaamd Majorana zero modes (MZM's) aan de grenzen. Vanwege hun niet-lokale correlatie en niet-Abelse statistische aard, MZM's worden voorgesteld als de qubits van topologische kwantumberekening. Vandaar, het zoeken en bedienen van de MZM's in TSC-materialen is nu een belangrijk onderwerp in de fysica van de gecondenseerde materie.
Om een TSC te identificeren, men moet eerst de topologische classificatie ervan vaststellen. De topologische classificatie hangt sterk af van de symmetrieën, waaronder tijdomkeringssymmetrie, deeltje-gat symmetrie, en vooral de kristallijne symmetrieën. Zonder rekening te houden met kristallijne symmetrieën, de Bogoliubov-deGennes (BdG) Hamiltonianen van de 1-D supergeleiders hebben alleen de Z2-classificatie. De spiegelreflectiesymmetrie en rotatiesymmetrie kunnen de classificatie naar Z-klasse verbeteren. Hoe dan ook, de topologische classificatie van supergeleiders met algemene magnetische symmetrieën is nog een open vraag.
In een nieuw onderzoeksartikel gepubliceerd in het in Peking gevestigde Nationale wetenschappelijke recensie , wetenschappers van de Huazhong University of Science and Technology in Wuhan, China, en Princeton University in New Jersey, USA stelde de methode voor om de topologische supergeleidende fase te classificeren door de compatibiliteit tussen verschillende MZM's te onderzoeken. Co-auteurs Jinyu Zou, Qing Xie, Zhida Song en Gang Xu analyseerden de topologische classificatie van gapped supergeleidende draden met lokale magnetische symmetrieën (LMS's). Ze ontdekten dat een effectieve BDI-klasse TSC kan worden gerealiseerd in M x T of C 2z T invariante draad. Opmerkelijk, de nieuwe TSC fasen gekenmerkt door Zh invariant in C 4z T-geval en Zhoplus Zc-invariant in C6zT-geval worden ontdekt.
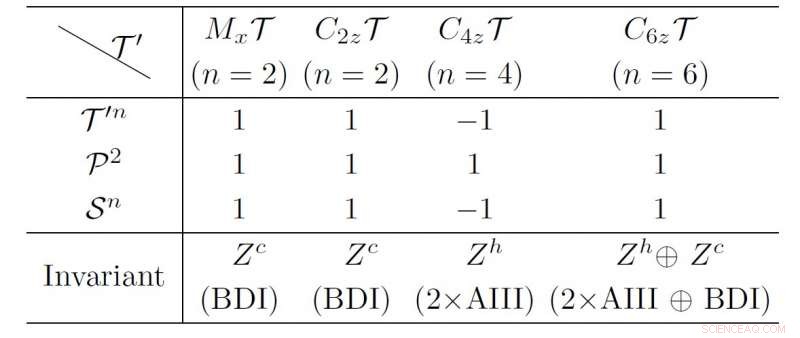
De topologische classificatie van de 1D hiaten supergeleidende systemen met de LMS's. Krediet:©Science China Press
In het artikel getiteld "Nieuwe typen topologische supergeleiders onder lokale magnetische symmetrieën". De auteurs richten zich op de 1D supergeleidende draden met LMS's T'=M x T, C 2z T, C 4z T en C 6z T. "De werking van T' verandert de positie van elektronen niet. Daarom werkt het op de BdG Hamiltoniaan als een tijdomkeringsoperator". Het combineren van T' en deeltje-gat symmetrie P leidt tot een chirale symmetrie S =T'P. De BdG Hamiltoniaan kan de diagonale vorm aannemen volgens de chirale symmetrie. En de MZM's zijn de eigentoestanden van de chirale symmetrie S. De auteurs vinden "MZM's met chirale eigenwaarden s en -s kunnen aan elkaar worden gekoppeld en worden geëlimineerd." Naar aanleiding van de richtlijn, ze analyseren de compatibiliteit van de MZM's aan het einde van de 1D supergeleidende draden met LMS'en, en vat hun topologische classificatie samen zoals vermeld in tabel I.
Hen x T en C 2z T-gevallen zijn gelijk aan de BDI-klasse met chirale topologische invariant Zc. Terwijl de C4zT-behuizing wordt gekenmerkt door spiraalvormige Z H onveranderbaar, die meerdere Majorana Kramer-paren aan het uiteinde van de supergeleidende draad aangeven. in de C 6z T geval, "de topologie van de hele BdG Hamiltoniaan is geclassificeerd door Z H plus Z C , ". In zo'n nieuwe topologische fase, "de spiraalvormige en chirale MZM's kunnen naast elkaar bestaan."
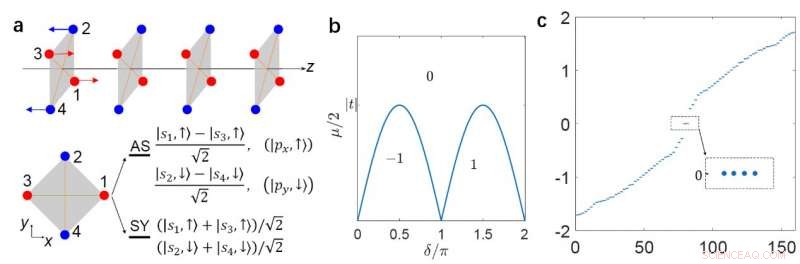
(a) Een C4zT-behoudende supergeleidende draad uitgelijnd in de z-richting. (b) Het topologische fasediagram. (c) het spectrum van niet-triviale fase met een open grens aan beide zijden, waarin vier MZM's verschijnen bij nul energie. Krediet:©Science China Press
"Om de TSC-fase te illustreren met de LMS C 4z T, we construeren een 1D anti-ferromagnetische keten langs de z-richting, " voegen de wetenschappers toe. Ze geven het topologische fasediagram van het model. "In de niet-triviale TSC-fase, de open kwantumdraad vangt een geheel aantal MZM's aan de uiteinden." ze tonen ook de MZM's door middel van numerieke en analytische berekening.
"Deze resultaten verrijken niet alleen de variëteit van de 1-D TSC, maar bieden ook weelderige bouwstenen voor de constructie van nieuwe type 2-D en 3-D TSC's", voorspellen ze aan het einde van het artikel, "Bijvoorbeeld, men kan de 1D TSC's in y-richting koppelen om een 2D TSC te construeren. De hoge symmetrielijnen ky =0 en ky =pi in de impulsruimte behouden de 1D LMS. Met de juiste parameters, de lijnen ky =0 en ky =pi kunnen tot een afzonderlijke topologische fase behoren, en resulteren in de gapless propagerende Majorana-randtoestanden die de geleidende banden en valentiebanden verbinden."
 Nieuwe methode ontdekt om eiwitten in menselijke cellen te bekijken
Nieuwe methode ontdekt om eiwitten in menselijke cellen te bekijken Slim papier kan elektriciteit geleiden, water detecteren
Slim papier kan elektriciteit geleiden, water detecteren Industriële verbinding krijgt milieuvriendelijke reactie
Industriële verbinding krijgt milieuvriendelijke reactie Onderzoekers produceren kosteneffectieve, milieuvriendelijk glasmateriaal
Onderzoekers produceren kosteneffectieve, milieuvriendelijk glasmateriaal Supersimulaties bieden nieuw inzicht in serotoninereceptoren
Supersimulaties bieden nieuw inzicht in serotoninereceptoren
 Kooldioxideniveaus bereikten 50% hoger dan pre-industriële tijd
Kooldioxideniveaus bereikten 50% hoger dan pre-industriële tijd Icy Ocean Worlds seismometer doorstaat verdere tests in Groenland
Icy Ocean Worlds seismometer doorstaat verdere tests in Groenland Klimaatgedreven evolutie in bomen verandert hun ecosystemen
Klimaatgedreven evolutie in bomen verandert hun ecosystemen NASA ziet tyfoon Phanfone aan land komen op de Filippijnen
NASA ziet tyfoon Phanfone aan land komen op de Filippijnen Twee Korea's op scherp terwijl tyfoon schiereiland nadert
Twee Korea's op scherp terwijl tyfoon schiereiland nadert
Hoofdlijnen
- Maak een lijst van de stappen van de celcyclus in volgorde
- Wat zijn drie primaire doelen van mitose?
- Hoeveel chromosomen zijn er in cellen van het menselijk lichaam?
- Kleine Braziliaanse kikkers zijn doof voor hun eigen roep
- Migratie maakt broeden moeilijker voor zeevogels
- Brandende chili houdt olifanten op afstand, nieuwe studie vondsten
- Hoe beïnvloeden het uitsterven van andere wezens mensen direct?
- Welke vier dingen maken ribosomen anders dan organellen?
- Hoe kolonies in de microbiologie te tellen
- Zoeken naar onzichtbare axion donkere materie met een holte met meerdere cellen
- Studie onthult nieuwe details over wat er gebeurde in de eerste microseconde van Big Bang

- Wetenschappers bieden voor het eerst een beeld van een ongrijpbare energie-explosie

- De punten verbinden voor kwantumnetwerken

- Marie Curie en haar bijdrage aan de slagveldgeneeskunde van de Eerste Wereldoorlog

 Breuken met decimalen vereenvoudigen
Breuken met decimalen vereenvoudigen  Ultradunne digitale camera geïnspireerd op Xenos peckii-ogen
Ultradunne digitale camera geïnspireerd op Xenos peckii-ogen Hoe NITS naar LUX
Hoe NITS naar LUX Waarom al dat geroezemoes over de supermaan?
Waarom al dat geroezemoes over de supermaan? Tsjernobyl verwelkomt toeristen in de Reactor 4-controlekamer (voor enkele minuten)
Tsjernobyl verwelkomt toeristen in de Reactor 4-controlekamer (voor enkele minuten)  Ontwikkelingen voor gemengd gebruik kunnen de betaalbaarheid van woningen zelfs verminderen, sociale diversiteit
Ontwikkelingen voor gemengd gebruik kunnen de betaalbaarheid van woningen zelfs verminderen, sociale diversiteit Onderzoekers racen tegen uitsterven om kankerbestrijdende eigenschappen van bomen te ontdekken
Onderzoekers racen tegen uitsterven om kankerbestrijdende eigenschappen van bomen te ontdekken Amerikaanse tarieven bedreigen buitenlandse autofabrikanten
Amerikaanse tarieven bedreigen buitenlandse autofabrikanten
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Spanish | Swedish | Dutch | Danish | Norway | Italian | Portuguese | German |

-
Wetenschap © https://nl.scienceaq.com

