
Wetenschap
Illusieve patronen in wiskunde verklaard door ideeën in de natuurkunde
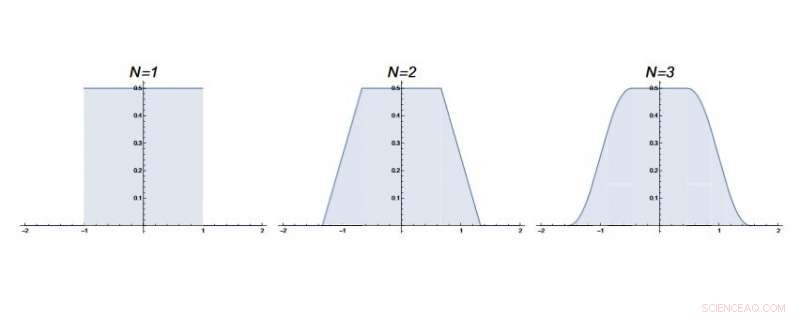
De “erosie” van de kansdichtheid van willekeurige wandelaars bij de oorsprong bij de achtste tijdstap (N ≥ 8, niet getoond) biedt enige fysieke intuïtie waarom een patroon in sommige Borwein-integralen plotseling op hetzelfde punt breekt. Krediet:Majumdar en Trizac. ©2019 American Physical Society
Patronen komen overal in de natuur en wiskunde voor, van de Fibonacci-spiralen van zeeschelpen tot de periodiciteit van kristallen. Maar bepaalde wiskundige problemen kunnen de menselijke oplosser soms misleiden om een patroon te zien, maar dan, uit het niets, het patroon verdwijnt plotseling. Deze ongrijpbare patronen duiken op in veel gebieden van wiskunde, met één voorbeeld afkomstig van bepaalde calculusintegralen die de intuïtie van zelfs de beste wiskundigen hebben bedrogen.
Nu in een nieuwe studie, twee natuurkundigen hebben deze integralen benaderd met behulp van het natuurkundige concept van willekeurige wandelingen. Terwijl het oplossen van deze integralen meestal veel inspanning en vindingrijkheid vereist, de natuurkundigen hebben aangetoond dat de nieuwe aanpak intuïtief en soms zelfs zonder expliciete berekeningen tot oplossingen kan komen.
Natuurkundigen Satya N. Majumdar en Emmanuel Trizac aan de Universiteit van Parijs-Sud, CNRS, In Frankrijk, hebben een artikel gepubliceerd over het gebruik van random walkers om integralen op te lossen in een recent nummer van: Fysieke beoordelingsbrieven.
"We hebben aangetoond dat natuurkundig inzicht ons in staat stelt om op een rekenvrije manier een schat aan merkwaardige integralen te verkrijgen, en bovendien, om voorheen onbekende identiteiten te verkrijgen (integraal, of gelijkheden tussen discrete sommen en integralen), " vertelde Trizac Phys.org . "Ons werk onthult dat wanneer wiskundige intuïtie wordt bedrogen, fysieke intuïtie kan de dag redden."
Patronen in Borwein-integralen
De betreffende integralen (zie figuur) zijn "Borwein-integralen, " genoemd naar David en Jonathan Borwein (vader en zoon), die in 2001 ongebruikelijke patronen in hen opmerkte. De Borwein-integralen hebben betrekking op het product van sinc (hoofdsinus) functies, die wijdverbreide toepassingen hebben, zoals in de optica, signaalverwerking, en andere gebieden. Deze twee specifieke integralen kunnen worden gebruikt om de volumes van hyperkubussen te berekenen.
Het oplossen van de Borwein-integralen omvat het vervangen van getallen in de variabele N . Elk getal geeft een andere oplossingswaarde, waardoor wiskundigen patronen kunnen waarnemen in de resulterende reeks waarden. Bijvoorbeeld, voor de eerste integraal (I N ), wanneer je de cijfers vervangt N =1-7, je krijgt elke keer het antwoord π. Maar als je bij N =8, het antwoord is iets minder dan π (ongeveer π – 10 -10 ). De eerste keer dat wiskundigen deze waarde op een computer berekenden, ze dachten dat er een bug in de software moest zitten. Maar het antwoord werd bevestigd, en de volgende voorwaarden (voor N =9, 10, enz.) steeds iets kleiner worden.

Krediet:Majumdar en Trizac. ©2019 American Physical Society
Sommige patronen blijven zelfs langer bestaan. Voor de tweede integraal, J N , de eerste 56 termen van de reeks (verkregen door de nummers 1 tot en met 56 te vervangen door N ) zijn allemaal π/2. Maar de 57 e termijn is ongeveer π/2-10 -110 , en de daaropvolgende termijnen blijven afnemen. (Het kan nog extremer worden:voor één variant van de Borwein-integralen - die hier niet wordt besproken - geldt een patroon van constante waarden voor een verbazingwekkende eerste 10 176 termen van de reeks, waarna het patroon uiteindelijk breekt.)
Wiskundigen kunnen verklaren waarom deze patronen plotseling doorbreken, althans in wiskundige termen. Merk op dat beide Borwein-integralen hierboven de functie sinc(a .) bevatten N k), waar een N =1/(2n-1). Als u de cijfers 1 vervangt, 2, 3, … voor N in deze uitdrukking, je krijgt de reeks 1, 1/3, 1/5, 1/7, 1/9, ... . De Borweins merkten dat de eerste termijn, 1, is niet alleen groter dan alle andere termen die erna komen, maar het is zelfs groter dan de som van de volgende paar termen - de tweede tot en met zevende termen, Om precies te zijn, als 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/13 =0,955… , wat kleiner is dan 1. Maar bij het toevoegen van de achtste term, 1/15, voor dit bedrag, het antwoord is 1.02…, dus net boven 1. Het blijkt geen toeval te zijn dat de zevende term de laatste term is waarvoor de integraal evalueert tot π, en de achtste term is het punt waarop het patroon breekt.
De Borweins bewezen een stelling (zie figuur) die dit idee in meer algemene termen verwoordt. De stelling geldt voor de tweede integraal, J N , ook. Rekening houdend met de cosinusfunctie in J N verandert de bovenstaande uitdrukking in 2/(2n-1), vanwege de eigenschap cos(a)sinc(a) =sinc(2a), zodat de eerste term 2 is in plaats van 1. Als de som van de tweede tot en met 56 e termen van de uitdrukking is kleiner dan 2, maar het toevoegen van de 57 e term duwt de som over 2, de stelling geldt.
Willekeurige wandelaars
Hoewel de stelling helpt verklaren wanneer de tijdelijke patronen van de Borwein-integralen breken, het is nog steeds niet helemaal duidelijk waarom de stelling in de eerste plaats geldt.
In de nieuwe krant Majumdar en Trizac hebben enige fysieke intuïtie in de stelling aangeboden door het te verbinden met een aantal goed begrepen concepten in kansrekening en statistische mechanica. Ze merkten op dat de integraal in de stelling nauw verband houdt met de uniforme kansverdeling, die veel wordt gebruikt in de wetenschap. specifiek, de Fourier-transformatie van de uniforme kansverdeling is toevallig gewoon de sinc-functie, wat de Borwein-integraal oplevert voor N =1. Deze verbinding overbrugt de Borwein-integralen naar de fysieke wereld, zodat met behulp van relevante parameters, gebeurtenissen die een uniforme verdeling volgen, kunnen worden gebruikt om de reeks oplossingen voor de Borwein-integralen te modelleren.
Om deze verbinding in een meer fysieke context te beschrijven, de onderzoekers keken naar willekeurige wandelaars. Een random walker is een abstract object dat een bepaalde afstand in elke richting kan verplaatsen, waarbij de exacte afstand willekeurig wordt gekozen uit een continu interval van waarden, en elk van deze waarden zal even waarschijnlijk worden gekozen (d.w.z. het volgt een uniforme verdeling). Willekeurige wandelaars kunnen een verscheidenheid aan willekeurige verschijnselen nauwkeurig modelleren, zoals beurskoersen, de paden van foeragerende dieren, en de paden van moleculen in een gas, die voorkomen in een, twee, of drie dimensies, respectievelijk.
In de nieuwe krant the physicists show that the movements of infinitely many random walkers can be used to model the emergence and disappearance of the patterns in the Borwein integrals. To begin, the random walkers all start at the point zero on the one-dimensional number line. For the first step, each walker is allowed to move a random distance of up to 1 unit, either left or right. For the second step, each walker may move a random distance of up to 1/3, then a random distance of up to 1/5, then 1/7, 1/9, etc. That is, each successive allowable step distance corresponds to the next value of the expression 1/(2n—1).
The main question is, what is the fraction of random walkers at the starting point (the origin) after each time step? It turns out that the fraction (more precisely, the probability density) of walkers at the origin at each time step N corresponds to the solution to the Borwein integral using the same N waarde.
As the physicists explain, for the first seven steps, the probability density that a walker ends up at the origin is always ½, which via the theorem above corresponds to an integral value of π. The key idea is that, up to this time, the density of walkers at the origin is the same as if the entire number line was uniformly populated with walkers. In werkelijkheid, as the maximum distance of each step is restricted, only part of the number line is accessible, d.w.z., the walkers' world is finite.
Echter, for the first seven steps, the walkers at the origin perceive that their world is infinite, since they do not possess any information about the existence of boundaries that would indicate that the world is finite. This is because none of those walkers that reached the outer boundary of their world (+1 or -1 after the first step) would have been able to make it back to the starting point in less than seven steps, even if taking the maximum size steps allowed and all in the direction toward the starting point. As these walkers had zero probability of showing up at the starting point before the eighth step, they could not affect the fraction of random walkers at the starting point. So for the first seven steps, the density of walkers at the origin is fixed at ½ (it is "protected").
But once those walkers that have reached +1 or -1 return to the origin, the situation changes. After the eighth step, it's possible that some of these walkers return to the starting point. Now these walkers act as "messengers" in the sense that their return to the starting point reveals the existence of a boundary, telling the other walkers at the origin that their world is finite, and therefore influencing the density of walkers at the origin.
Since these messenger walkers made it back to the starting point, it becomes clear that some other boundary-reaching walkers did not make it back, but instead may have kept continuing to move further away. Als resultaat, the probability distribution becomes more spread out, causing the fraction of walkers at the origin to gradually erode from ½ (or π for the integral). It is this erosion that explains why the values of the first Borwein integral decrease ever so slightly for n ≥ 8. A similar argument holds for the second Borwein integral (see video).
By connecting the Borwein integrals to the probabilities of random walkers, the new results offer a completely different approach to solving these integrals than through direct calculation. The physicists showed that the same approach can be applied to many other integrals in addition to the two described here, including extensions to higher dimensions. The researchers expect that the approach has the potential to provide calculation-free solutions to many other integrals that are otherwise very difficult to solve.
"Random walk problems and their infinite ramifications form one of the cornerstones of modern physics with a wide range of applications in physics, chemistry, biologie, Engineering, enzovoort., " Trizac said. "Since our derivation of intriguing integrals involves basic concepts from random walk theory, we expect that new identities and integrals, with real-world applications, may be derived using our key idea in the near future."
© 2019 Wetenschap X Netwerk
 Hoe het aantal ionen in een verbinding te vinden
Hoe het aantal ionen in een verbinding te vinden  Onderzoek naar aluminiumlegeringen kan bemande ruimtemissies ten goede komen
Onderzoek naar aluminiumlegeringen kan bemande ruimtemissies ten goede komen Oude eiwitten vertellen verhalen over historische artefacten en de mensen die ze hebben aangeraakt
Oude eiwitten vertellen verhalen over historische artefacten en de mensen die ze hebben aangeraakt Wanneer meer botvormende cellen gelijk zijn aan minder bot
Wanneer meer botvormende cellen gelijk zijn aan minder bot Vastestofkatalyse:fluctuaties maken de weg vrij
Vastestofkatalyse:fluctuaties maken de weg vrij
 Het verschil tussen Wespen en Bees
Het verschil tussen Wespen en Bees Zelfs een beperkte kernoorlog tussen India en Pakistan zou leiden tot wereldwijde hongersnood, zegt studie
Zelfs een beperkte kernoorlog tussen India en Pakistan zou leiden tot wereldwijde hongersnood, zegt studie Industriële brom in de VS in kaart brengen
Industriële brom in de VS in kaart brengen Enorme vulkaanuitbarsting veroorzaakte 140 miljoen jaar geleden geen klimaatverandering en massale uitsterving
Enorme vulkaanuitbarsting veroorzaakte 140 miljoen jaar geleden geen klimaatverandering en massale uitsterving Grootte is belangrijk voor bio-energie met koolstofafvang en -opslag
Grootte is belangrijk voor bio-energie met koolstofafvang en -opslag
Hoofdlijnen
- Hoe maak je een 3D-model van het spierstelsel voor een wetenschapsklasse
- De isovormen van het HP1-eiwit reguleren de organisatie en structuur van heterochromatine
- Wie eet wie? Hoe klimaatverandering de interacties tussen vissen en roofdieren verandert
- Nieuwe vogelsoort genoemd naar Harvard-vader van biodiversiteit
- Het verschil tussen genomisch DNA en plasmide DNA
- Wat zijn de gespecialiseerde cellen die vasculair weefsel vormen?
- Wie ontdekte de nucleaire envelop?
- Hoe te differentiëren tussen mitose en cytokinese
- Wat is Serum?
- Maak kennis met AFM: de verbijsterende nieuwe ziekte Sommige artsen noemen de "Nieuwe Polio"
- Londenaren voelen zich genegeerd en niet vertegenwoordigd door advertenties

- Nieuw ontdekt fossiel toont kleinschalige evolutionaire veranderingen in een uitgestorven menselijke soort

- Toerisme wil wanhopig terug naar het oude normaal, maar dat zou een ramp zijn

- Samenlevingen kunnen de vertegenwoordiging van vrouwen binnen de academische wetenschap helpen bevorderen

 Een omgekeerd ecosysteem in de Arabische Zee
Een omgekeerd ecosysteem in de Arabische Zee VN bevestigt Madrid als nieuwe locatie voor klimaattop
VN bevestigt Madrid als nieuwe locatie voor klimaattop Onderzoekers ontwikkelen nieuwe ultrasnelle 3D-microscoop
Onderzoekers ontwikkelen nieuwe ultrasnelle 3D-microscoop Onderzoek toont aan dat sociale media een effectief hulpmiddel zijn om stemresultaten te voorspellen
Onderzoek toont aan dat sociale media een effectief hulpmiddel zijn om stemresultaten te voorspellen Millennials zijn het meest getroffen door de krapte in de middenklasse:OESO
Millennials zijn het meest getroffen door de krapte in de middenklasse:OESO Hoe de viskweekindustrie klimaatvriendelijker te maken?
Hoe de viskweekindustrie klimaatvriendelijker te maken? Natuurkundigen ontdekken nieuw elektronisch fenomeen
Natuurkundigen ontdekken nieuw elektronisch fenomeen Onderzoekers ontwikkelen plantaardige technologie die biobrandstoffen helpt, kan kanker bestrijden
Onderzoekers ontwikkelen plantaardige technologie die biobrandstoffen helpt, kan kanker bestrijden
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Swedish | German | Dutch | Danish | Norway | Portuguese |

-
Wetenschap © https://nl.scienceaq.com

