Hoe bewijs je iets? Wat is zelfs bewijs?

In de wetenschap, het woord "bewijs" wordt zelden en met grote zorg gebruikt. Wetenschappers accepteren dat de natuurlijke wereld vol verrassingen is, en wat waar lijkt te zijn, kan uitzonderingen hebben.

In de rechtbanken, bewijs bevat vaak een waarschuwing, zoals "on the balance of probabilities" voor burgerlijke zaken, en "buiten redelijke twijfel" voor strafzaken.

Maar voor wiskundigen zoals Dr. Nick Beaton van de Universiteit van Melbourne, Professor Jan de Gier en Professor Tony Guttmann, "buiten redelijke twijfel" is gewoon niet goed genoeg. Naar hen, een wiskundig bewijs is "zonder enige twijfel" - en het is iets moois.

Denk aan de stelling van Pythagoras.

We leren allemaal op school dat het kwadraat van de langste zijde van een rechthoekige driehoek de som is van de kwadraten van de twee andere zijden. Je kunt dit testen met een stuk papier, een liniaal en een rekenmachine, en je zult zien dat het waar is.

Je zou dit voor duizend driehoeken kunnen doen en je zult zien dat het waar is voor elk van die duizend driehoeken.

Maar werkt de stelling van Pythagoras voor elke mogelijke rechthoekige driehoek?

Je kunt niet elke bestaande rechthoekige driehoek meten, dus de methode van liniaal en rekenmachine kan Pythagoras niet definitief bewijzen.

"Je doet veel simulaties en je observeert een bepaald ding numeriek, en als je dat keer op keer observeert, zou je denken dat dat waarschijnlijk altijd het geval is, of het is waar, " zegt Dr. Nick Beaton.

"Maar dat is niet helemaal hetzelfde als een wiskundig bewijs hebben waarmee je eigenlijk logisch kunt aantonen dat iets altijd gebeurt bij bepaalde waarden van de parameters."

Zonder formeel wiskundig bewijs, we noemen zoiets als de stelling van Pythagoras een vermoeden.

Professor De Gier zegt dat een vermoeden in de wiskunde een resultaat is waarvan iedereen gelooft dat het waar is.

"Maar het is niet logisch bewezen in strikte zin, " hij zegt.

"Dus, er kan veel numeriek bewijs zijn en er kunnen sterke en overtuigende argumenten zijn, maar ze stellen geen onomstotelijke waarheid vast.

"Een goed voorbeeld is de Riemann-hypothese over de nullen van de zeta-functie, die is gecontroleerd voor de eerste 10, 000, 000, 000, 000 (tien biljoen) gevallen. Een bewijs dat het waar is voor elk geval ontbreekt nog en is een miljoen dollar waard, ’ zegt professor De Gier.

"Bewijzen dat het licht zou werpen op veel van de mysteries rond de verdeling van priemgetallen."

"En af en toe ziet iets er heel overtuigend uit, maar dan wordt het getoond, als je eenmaal tot in de kleinste details bent doorgedrongen, dat het eigenlijk niet geldt en er kunnen uitzonderingen zijn."

Wikipedia heeft zelfs een categorie voor 'weerlegde vermoedens' - sommige, zoals het vermoeden van Euler, heeft honderden jaren gestaan ​​voordat het werd weerlegd.

In het geval van de stelling van Pythagoras, echter, het bewijs is al duizenden jaren bij ons. In feite, Pythagoras heeft de formule niet uitgevonden, het was al lang voor zijn tijd bekend. Hij kwam met het eerste bekende bewijs.

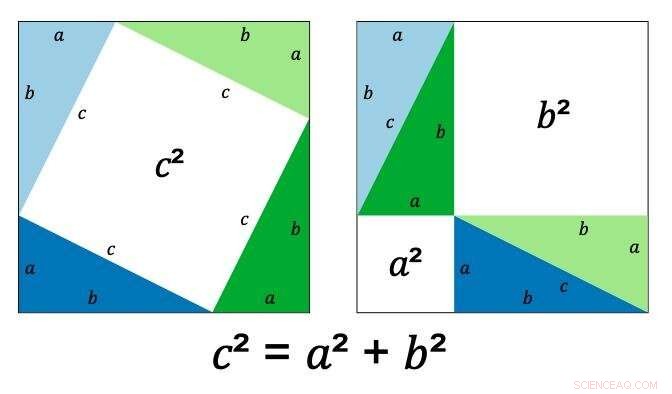
Het bewijs van Pythagoras maakt gebruik van het onbetwistbare feit dat elke rechthoekige driehoek kan worden weergegeven door twee vierkanten, de een in de ander, waarbij de hoeken van het binnenste vierkant de rand van het buitenste raken.

Het binnenste vierkant heeft zijden van lengte c (de werkelijke lengte doet er niet toe omdat c elk positief getal kan zijn), het buitenste vierkant heeft lengte a+b, en de driehoek die het maakt heeft lengtes a, b en c (zoals afgebeeld).

Als u de hoek van het binnenvierkant verandert, verandert de lengte van alle drie de waarden.

Pythagoras toonde aan dat door de driehoeken binnen het vierkant te herschikken, het witte gebied, weergegeven door c² in het bovenstaande diagram, wordt twee vierkanten, één met oppervlakte a² en één met oppervlakte b². Vandaar, c² is altijd, welke afmetingen je ook gebruikt, gelijk aan a²+b².

Sinds Pythagoras, wiskundigen zijn door de eeuwen heen doorgegaan met het vinden van bewijzen voor de stelling. 1940, De Amerikaanse wiskundige Elisha Scott Loomis publiceerde een verzameling bewijzen van de stelling van Pythagoras.

Het team van de Universiteit van Melbourne is geen onbekende in bewijzen.

De Australian Mathematical Society kende in 2018 de Gavin Brown Prize voor beste paper toe aan Dr. Beaton, Professor de Gier en Professor Guttman, samen met Mireille Bousquet-Mélou van de Université de Bordeaux in Frankrijk en Hugo Duminil-Copin van de Université de Genève in Zwitserland, voor een wiskundig bewijs uit 2015 van het bestaan ​​en de kritische oppervlaktespanning voor adsorptie van polymeren (langeketenmoleculen) in oplossing.

Het team gebruikte een wiskundige weergave van een polymeer, een "zelfmijdende wandeling" genoemd, ", dit zijn objecten die worden gebruikt in een tak van de wiskundige fysica die statistische mechanica wordt genoemd.

"Een zelfvermijdende wandeling is een wandeling op een rooster - vaak een vierkant rooster of een honingraatrooster - waar je geen van de stappen die je hebt gezet kunt terugvinden, " zegt professor Guttmann.

"Je kunt één wandeling zien als een enkele polymeer, met willekeurige eigenschappen."

Dr. Beaton zegt dat, vaak, het vinden van een wiskundig bewijs voor een vermoeden is een lange, moeilijk proces, met vallen en opstaan, grommend werk en af ​​en toe een eureka-moment.

Voor Pythagoras, het eureka-moment was de vierkant-in-vierkant weergave van de driehoek; voor het Melbourne-team en hun collega's, het was de beste manier vinden om wiskundig met de willekeur om te gaan.

"Mensen probeerden een paar dingen toen het voor het eerst werd vermoed, maar niemand kwam veel vooruit, dus het was duidelijk dat er een nieuw idee nodig was, maar wat dat nieuwe idee zou moeten zijn, was niet duidelijk, ’ zegt professor De Gier.

Na enkele doodlopende wegen te hebben gevolgd, het team concentreerde zich op een nieuw idee in de wiskunde in verband met roostermodellen, genaamd "discrete holomorfiteit, " die werd gepopulariseerd door de Russische onderzoeker professor Stanislav Smirnov die in 2010 de Fields-medaille won voor uitstekende ontdekkingen in de wiskunde.

Met behulp van deze nieuwe vorm van wiskunde, het Melbourne-team ontdekte dat het honingraatrooster de juiste instelling was om hun polymeerprobleem te bewijzen.

"Om de een of andere reden, de wiskunde van zelfmijdende wandelingen op een honingraatrooster is mooi gelukt, ’ zegt professor de Gier.

"Als je dit op een vierkant rooster wilt doen, het werkt niet, maar voor andere problemen het vierkante rooster zou beter zijn."

Professor de Gier zegt dat een wiskundig bewijs niet alleen een intellectuele oefening is, het kan ons fundamentele dingen over de natuur vertellen.

"Het is interessant om te weten dat iets gebeurt of waar het gebeurt, maar het hebben van die logische redenering is interessanter omdat het inzicht geeft in waarom dingen gebeuren zoals ze gebeuren."