
Wetenschap
Wiskunde van schaal:Groot, klein en alles daartussenin

Hoeveel meren zijn er in Alaska? Thermokarst-meren op de noordhelling van Alaska lijken op elkaar en zijn fractaal. Krediet:schilderij van Cherissa Dukelow, CC BY-SA
Ademen. Als je longen uitzetten, lucht vult 500 miljoen kleine longblaasjes, elk een fractie van een millimeter breed. Terwijl je uitademt, deze miljoenen kleine ademhalingen smelten moeiteloos samen door steeds grotere luchtwegen tot één ultieme ademhaling.
Deze luchtwegen zijn fractaal.
Fractals zijn een wiskundig hulpmiddel voor het gedetailleerd beschrijven van objecten op elke schaal. Wiskundigen en natuurkundigen zoals ik gebruiken fractals en gerelateerde concepten om te begrijpen hoe dingen veranderen van klein naar groot.
Jij en ik vertalen tussen enorm verschillende schalen als we nadenken over hoe onze keuzes de wereld beïnvloeden. Draagt deze latte bij aan klimaatverandering? Moet ik stemmen bij deze verkiezingen?
Deze conceptuele instrumenten zijn zowel van toepassing op het lichaam als op landschappen, natuurrampen en de samenleving.
Fractals overal
In 1967, wiskundige Benoit Mandelbrot vroeg:"Hoe lang is de kust van Groot-Brittannië?"
Het is een strikvraag. Het antwoord hangt af van hoe je het meet. Als u de omtrek op een kaart volgt, je krijgt één antwoord, maar als je langs de kustlijn loopt met een meterstok, het resultaat is heel anders. Iedereen die heeft geprobeerd de lengte van een ruig wandelpad vanaf een kaart in te schatten, kent het verraad van het grootschalige beeld.
Dat komt omdat longen, de Britse kustlijn en wandelpaden hebben allemaal fractaliteit:hun lengte, aantal takken of een andere hoeveelheid hangt af van de schaal of resolutie die u gebruikt om ze te meten.
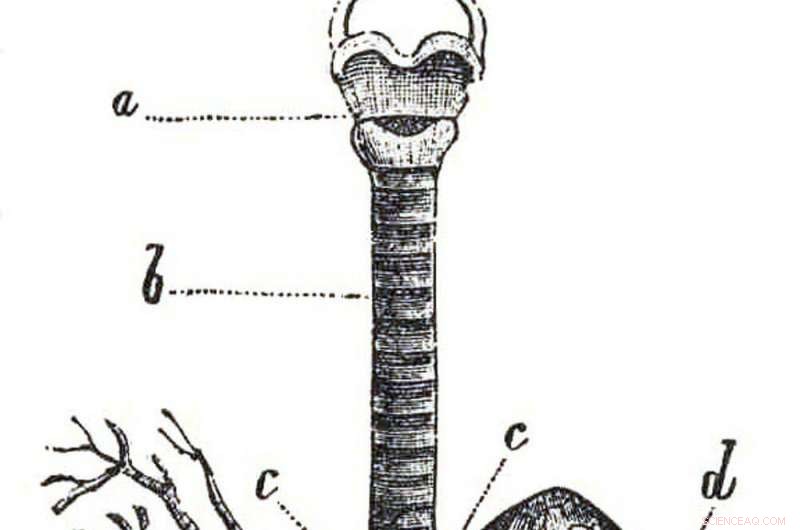
De takken in de longen zijn een voorbeeld van zelfgelijkenis. Krediet:Brockhaus en Efron Encyclopedic Dictionary/Wikimedia
De kustlijn lijkt ook op zichzelf:hij is gemaakt van kleinere kopieën van zichzelf. Varenbladeren, bomen, slakkenhuizen, landschappen, de silhouetten van bergen en riviernetwerken lijken allemaal op kleinere versies van zichzelf.
Dat is waarom, als je naar een luchtfoto van een landschap kijkt, het is vaak moeilijk te zeggen of de schaalbalk 50 km of 500 m moet zijn.
Je longen lijken op elkaar, omdat het lichaam elke tak nauwkeurig in exacte verhoudingen kalibreert, waardoor elke tak een kleinere replica van de vorige is. Dit modulaire ontwerp maakt longen efficiënt op elk formaat. Denk aan een kind en een volwassene, of een muis, een walvis. Het enige verschil tussen klein en groot is hoe vaak de luchtwegen zich vertakken.
Zelfgelijkenis en fractaliteit verschijnen in kunst en architectuur, in de bogen binnen bogen van Romeinse aquaducten en de torenspitsen van gotische kathedralen die het bladerdak weerspiegelen. Zelfs oude Chinese kalligrafen Huai Su en Yan Zhenqing waardeerden de fractaliteit van zomerwolken, scheuren in een muur en watervlekken in een lekkend huis in 722.
Schaalinvariantie
Zelfgelijkende objecten hebben een schaalinvariantie. Met andere woorden, sommige eigendommen blijven behouden, ongeacht hoe groot ze worden, zoals de efficiëntie van de longen.
In werkelijkheid, schaalinvariantie beschrijft wat er tussen schalen verandert door te zeggen wat niet verandert.

Satellietfoto van Groot-Brittannië en Noord-Ierland. Krediet:NASA
Leonardo da Vinci merkte op dat, als bomen vertakken, de totale dwarsdoorsnede van alle takken blijft behouden. Met andere woorden, van stam tot twijg gaan, het aantal takken en hun diameter veranderen met elke vertakking, maar de totale dikte van alle samengebundelde takken blijft hetzelfde.
Da Vinci's waarneming impliceert een schaalinvariantie:voor elke tak van een bepaalde straal, er zijn vier stroomafwaartse takken met de helft van die straal.
Aardbevingsfrequentie heeft een vergelijkbare schaalinvariantie, die werd waargenomen in de jaren 1940. De grote komen voor de geest:Lissabon 1755, San Francisco 1989, maar er vinden elke dag veel kleine aardbevingen plaats in Californië. De wet van Gutenberg-Richter zegt dat de frequentie van aardbevingen afhangt van de grootte van de aardbeving. Het antwoord is verrassend eenvoudig. Een tien keer grotere aardbeving komt ongeveer een tiende zo vaak voor.
Maatschappij en de machtswet
Een 19e-eeuwse econoom Vilifredo Pareto - beroemd in de business school vanwege de 80/20-regel - merkte op dat het aantal gezinnen met een bepaald vermogen omgekeerd evenredig is met hun vermogen, verhoogd tot een exponent. Pareto mat de exponent voor verschillende jaren en verschillende landen en ontdekte dat deze meestal rond de 1,5 lag.
De welvaartsverdeling van Pareto werd bekend als de machtswet. ogenschijnlijk vanwege de exponent of "macht".
Alles wat op zichzelf lijkt, heeft een overeenkomstige machtswet. In een aprilkrant mijn collega en ik beschrijven de bijbehorende machtswet voor longen, bloedvaten en bomen. Het verschilt alleen van de machtswet van Pareto door rekening te houden met specifieke verhoudingen tussen takken.
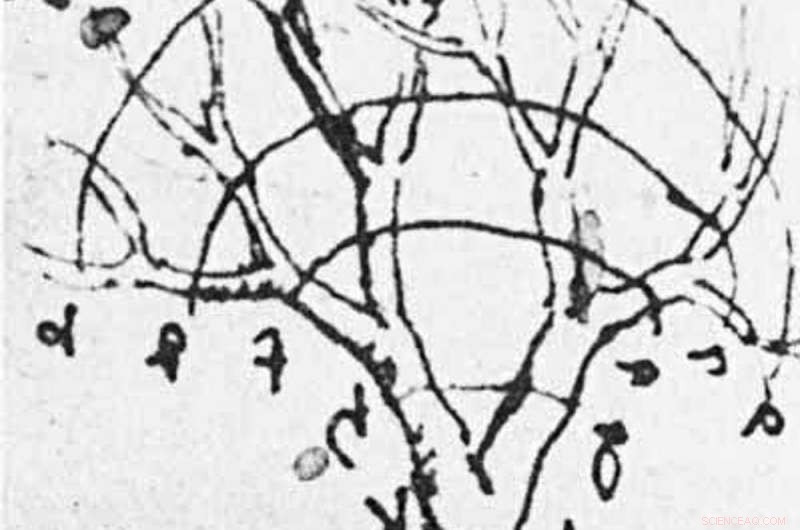
Een schets van Leonardo da Vinci's aantekeningen op boomtakken. Krediet:Fractal Foundation
De grootte van fortuinen is dan verwant aan de grootte van boomtakjes of bloedvaten - een paar stammen of grote takken en exponentieel meer kleine takjes.
Pareto beschouwde zijn verdeling van rijkdom als een natuurwet, maar veel verschillende modellen van sociale organisatie leiden tot een Pareto-verdeling en samenlevingen variëren in welvaartsongelijkheid. Hoe hoger de exponent van Pareto, hoe meer egalitair de samenleving.
Van het begrijpen hoe mensen zijn opgebouwd uit kleine cellen tot hoe we de planeet beïnvloeden, zelfgelijkenis, fractaliteit en schaalinvariantie helpen vaak bij het vertalen van het ene organisatieniveau naar het andere.
Dit artikel is opnieuw gepubliceerd vanuit The Conversation onder een Creative Commons-licentie. Lees het originele artikel. 
 Het onderwaterwonderland van Boedapest trekt duikers van heinde en verre
Het onderwaterwonderland van Boedapest trekt duikers van heinde en verre Kunnen onze bossen de volgende droogte overleven?
Kunnen onze bossen de volgende droogte overleven? NASA vindt zware regenval in tropische storm Hikaa
NASA vindt zware regenval in tropische storm Hikaa Oireachtas-commissie:boeren moeten opkomen voor het aanplanten van bossen om klimaatverandering aan te pakken
Oireachtas-commissie:boeren moeten opkomen voor het aanplanten van bossen om klimaatverandering aan te pakken Nul herstel voor koralen bij back-to-back bleking in Australië
Nul herstel voor koralen bij back-to-back bleking in Australië
Hoofdlijnen
- Vergelijking & identificatie van kikkers en menselijke bloedcellen
- Mensen gebruiken niet zoveel denkkracht als we graag denken
- Hoe hoge bomen suikers verplaatsen
- Is het tijd dat ons begrip van evolutie evolueert?
- Virussen bestrijden:codebrekers worden codeschrijvers
- Plasticity Cell Definition
- Welke organen helpen het menselijk lichaam om zich te ontdoen van door cellen geproduceerd afval?
- Onderzoekers identificeren een paar receptoren die essentieel zijn voor de communicatie tussen mannen en vrouwen bij planten
- Onderzoek onthult hoe klimaatverandering de aquacultuur van Hawaiiaanse visvijvers kan beïnvloeden
- Zwarte en Latinx-conservatieven verschuiven competentie naar blank publiek:studie

- Federale stimuleringshulp heeft de ongelijkheid tussen blanken en minderheden vergroot

- Archeologen vinden overblijfselen van tempel uit het Romeinse tijdperk in Egypte

- Tijden waarin we ons niet gedroegen, kunnen op de lange termijn nuttig zijn, studie vondsten

- 800 miljoen mensen gebruiken nu regelmatig Aziatische Engelsen

 End-to-end leren van het genereren van co-spraakgebaren voor humanoïde robots
End-to-end leren van het genereren van co-spraakgebaren voor humanoïde robots Kunnen koralen zich aanpassen aan klimaatverandering?
Kunnen koralen zich aanpassen aan klimaatverandering? Ruimtewandelende astronaut verliest spiegel, nieuwste ruimteafval
Ruimtewandelende astronaut verliest spiegel, nieuwste ruimteafval Hoe schaaldieren ademen?
Hoe schaaldieren ademen?  ESA's eerste satelliet:COS-B
ESA's eerste satelliet:COS-B Laatste gemeenschappelijke aap-menselijke voorouder was waarschijnlijk zo groot als een gibbon
Laatste gemeenschappelijke aap-menselijke voorouder was waarschijnlijk zo groot als een gibbon  Kinderen leren een thermometer te lezen
Kinderen leren een thermometer te lezen  Onderzoekers bedenken een schakelaar die de elektronica kan verbeteren
Onderzoekers bedenken een schakelaar die de elektronica kan verbeteren
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

