
Wetenschap
Een steen met een gewicht van 98 newton wordt 50 meter boven de grond van de rand van een brug geduwd. Wat was de kinetische energie halverwege de val?
$$KE =\frac{1}{2}mv^2$$
Waar KE kinetische energie is, is m de massa van het gesteente en v de snelheid ervan.
Eerst moeten we de snelheid van het gesteente halverwege vinden. We kunnen de bewegingsvergelijking gebruiken:
$$v^2 =u^2 + 2as$$
Waar:
- v is de eindsnelheid (halverwege)
- u is de beginsnelheid (0 m/s, aangezien het gesteente valt)
- a is de versnelling als gevolg van de zwaartekracht (-9,8 m/s²)
- s is de afgelegde afstand (de helft van de totale hoogte, 25 meter)
Als we de waarden invoeren, krijgen we:
$$v^2 =0 + 2(-9,8)(25)$$
$$v^2 =-490$$
$$v =\sqrt{-490} =22,14 \ m/s$$
Nu kunnen we de kinetische energie halverwege berekenen:
$$KE =\frac{1}{2}(98)(22.14)^2$$
$$KE =24.100 \ J$$
Daarom is de kinetische energie van het rek in het midden van zijn val 24.100 Joule.
 Wat staat voor staal op het periodiek systeem?
Wat staat voor staal op het periodiek systeem?  Onderzoek suggereert dat helium een oppasrol speelt bij het vormen van stabiele chemische verbindingen onder hoge druk
Onderzoek suggereert dat helium een oppasrol speelt bij het vormen van stabiele chemische verbindingen onder hoge druk Experiment leidt tot materiaal dat is aangepast voor gebruik bij watersplitsing op zonne-energie om waterstof te produceren
Experiment leidt tot materiaal dat is aangepast voor gebruik bij watersplitsing op zonne-energie om waterstof te produceren  Is asgas vloeibaar of vast?
Is asgas vloeibaar of vast?  Milk & Vinegar Experiment for a Science Fair
Milk & Vinegar Experiment for a Science Fair
 'Smerig en weerzinwekkend' of juwelen uit de natuurlijke wereld? De ingewikkelde geschiedenis van de mens-kikkerrelaties
'Smerig en weerzinwekkend' of juwelen uit de natuurlijke wereld? De ingewikkelde geschiedenis van de mens-kikkerrelaties  Door droogte geteisterde Australische boeren nu geteisterd door overstromingen
Door droogte geteisterde Australische boeren nu geteisterd door overstromingen Het volgen van veranderingen in de omvang van wetland kan helpen de snelheid van klimaatverandering te voorspellen
Het volgen van veranderingen in de omvang van wetland kan helpen de snelheid van klimaatverandering te voorspellen De ijsbergproductie meten met aardbevingen
De ijsbergproductie meten met aardbevingen Chemische cocktail gevonden in Barrier Reef-schildpadden
Chemische cocktail gevonden in Barrier Reef-schildpadden
Hoofdlijnen
- Filmen hoe ons immuunsysteem bacteriën doodt
- 5 stadia van mitose
- Sarcodina Life Cycle
- Iets om op te kauwen:Onderzoekers zoeken naar verbanden in de manier waarop dieren voedsel eten en verteren
- Hoe verschilt mitose in de cellen van dieren en planten?
- Nieuwe studie onthult waarom sommige bedreigde koralen 'algen'-partners ruilen
- In welk jaar bouwde Francis Crick het DNA-model?
- Zeeleeuwen hebben unieke snorharen waarmee ze zelfs de snelste vis kunnen vangen
- Gewoon een faag? Hoe de roofdieren van bacteriën het darmmicrobioom kunnen vormen
- Biomechanica van de kick-start-beweging bij wedstrijdzwemmen

- Milieuverliezen in kwantuminformatiesystemen vermijden

- Onderzoeker experimenteert met elektron-plasma-interacties

- Kwantumeffect veroorzaakt ongebruikelijke materiaaluitbreiding
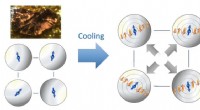
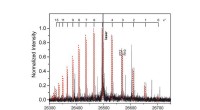
- Wetenschappers lossen een halve eeuw oud magnesiumdimeermysterie op
 Wat als we op de maan zouden leven?
Wat als we op de maan zouden leven?  Hoe leden van het microbioom specifiek Salmonella-infecties bestrijden
Hoe leden van het microbioom specifiek Salmonella-infecties bestrijden  Na de verwoesting van de cycloon, terug naar af voor Mozambiques Beira
Na de verwoesting van de cycloon, terug naar af voor Mozambiques Beira Licht op efficiëntieverlies in organische zonnecellen
Licht op efficiëntieverlies in organische zonnecellen Olijfolie en schimmel beschermen hout tegen houtrot
Olijfolie en schimmel beschermen hout tegen houtrot In Shawnee National Forest woedt een debat over de vraag hoe bomen het beste kunnen worden beschermd te midden van klimaatverandering en bosbranden
In Shawnee National Forest woedt een debat over de vraag hoe bomen het beste kunnen worden beschermd te midden van klimaatverandering en bosbranden  IceCube helpt bij het demystificeren van vreemde radio-uitbarstingen vanuit de verre ruimte
IceCube helpt bij het demystificeren van vreemde radio-uitbarstingen vanuit de verre ruimte Taalvaardigheden zijn van cruciaal belang voor het begrijpen van residentiële segregatie, zegt onderzoek
Taalvaardigheden zijn van cruciaal belang voor het begrijpen van residentiële segregatie, zegt onderzoek
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

