
Wetenschap
Een blok van 6 kg wordt 8 m omhoog geduwd in een grof hellend vlak met een horizontale kracht van 75 N als de beginsnelheid 2 ms en kinetische wrijving 25N de beweging tegenwerkt, wat dan?
$$W =Fd\cos\theta =(75 \text{ N})(8 \text{ m})\cos37° =466,51 \text{ J}$$
De arbeid die wordt verricht door de kracht van kinetische wrijving bij het tegenwerken van de beweging is:
$$W_f =-f_kd =-(25 \text{ N})(8 \text{ m}) =-200 \text{ J}$$
De verandering in de kinetische energie van het blok is:
$$\Delta K =K_f - K_i =\frac{1}{2}mv_f^2 - \frac{1}{2}mv_i^2$$
We kunnen het behoud van energie gebruiken om het werk van de krachten te relateren aan de verandering in kinetische energie:
$$W + W_f =\Delta K$$
Als we de waarden vervangen die we hebben berekend, krijgen we:
$$466,51 \text{ J} - 200 \text{ J} =\frac{1}{2}(6 \text{ kg})v_f^2 - \frac{1}{2}(6 \text{ kg} )(2 \text{ m/s})^2$$
Als we $v_f$ oplossen, krijgen we:
$$v_f =5,24 \text{ m/s}$$
Daarom is de snelheid van het blok aan het einde van de verplaatsing van 8 m 5,24 m/s.
 Simulaties laten zien dat ijzer de corrosie in 'inert' kooldioxide katalyseert
Simulaties laten zien dat ijzer de corrosie in 'inert' kooldioxide katalyseert  Welke van de volgende omschrijvingen beschrijft geen zuur?
Welke van de volgende omschrijvingen beschrijft geen zuur?  Welke mineralen bruisen als er zoutzuur op de mineralen valt?
Welke mineralen bruisen als er zoutzuur op de mineralen valt?  Wat blijkt uit de reactie ca2 plus aq 2oh-aq -- caoh2 s h16.71?
Wat blijkt uit de reactie ca2 plus aq 2oh-aq -- caoh2 s h16.71?  Nieuwe MD-simulatie werpt licht op het mysterie van de structuur van gehydrateerde elektronen
Nieuwe MD-simulatie werpt licht op het mysterie van de structuur van gehydrateerde elektronen
 Afbeelding:Lake Huron
Afbeelding:Lake Huron Winter in Nieuw-Zeeland warmste, natste ooit
Winter in Nieuw-Zeeland warmste, natste ooit Onderzoekers onderzoeken oorzaken van verandering van landbedekking in Afrikaanse savannes
Onderzoekers onderzoeken oorzaken van verandering van landbedekking in Afrikaanse savannes Opwarming van de aarde zal miljoenen meer blootstellen aan overstromingen
Opwarming van de aarde zal miljoenen meer blootstellen aan overstromingen Wetenschappers zeggen dat de kosten van het afvangen van CO2 afnemen
Wetenschappers zeggen dat de kosten van het afvangen van CO2 afnemen
Hoofdlijnen
- Bijenimiterende vliegen vertonen bestuiverpotentieel
- Team ontwikkelt nieuw type antistollingsmiddel waarvan de werking snel kan worden gestopt
- Hebben abiotische factoren invloed op biotische factoren?
- Wat is erytrocyanine?
- Onderzoekers ontdekken dat een klein organisme de kracht heeft om een hardnekkig broeikasgas op landbouwvelden te verminderen
- Frankrijk verzet zich tegen EU-verlenging van 5 jaar voor onkruidverdelger glyfosaat
- Hoe de hagedisstaart normaal intact kan blijven maar afbreekt wanneer dat nodig is
- Bacteriën voor klimaatneutrale chemicaliën van de toekomst
- Artikel geeft een gedetailleerd overzicht van deelnemers aan Golden Retriever Lifetime Study
- Natuurkundige creëert vijfde toestand van materie vanuit de woonkamer

- Wat een nooit eerder gezien radioactief verval ons kan vertellen over neutrino's

- Een model voor het beschrijven van de hydrodynamica van menigten

- Wetenschappers manipuleren de eigenschappen van kwantumstippen

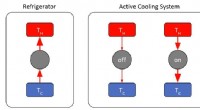
- Gebruik van metalen met een hoge thermo-elektrische vermogensfactor om een efficiënte, volledig actieve koeler te creëren
 Nanodeeltjes zijn van nature aanwezig in links- en rechtshandige versies
Nanodeeltjes zijn van nature aanwezig in links- en rechtshandige versies Langdurige pijnverlichting met MOF's
Langdurige pijnverlichting met MOF's Schuldspel over 830 miljoen euro schikking in VW's Duitse dieselzaken
Schuldspel over 830 miljoen euro schikking in VW's Duitse dieselzaken Een leraar, een spion, een schild - dit nanodeeltje draagt veel hoeden in het lichaam
Een leraar, een spion, een schild - dit nanodeeltje draagt veel hoeden in het lichaam Supply chain-innovatie kan voedseltekorten door coronavirus verminderen
Supply chain-innovatie kan voedseltekorten door coronavirus verminderen Welke aanvullende informatie is nodig om de molecuulformule te berekenen op basis van het massapercentage van elk element in een verbinding?
Welke aanvullende informatie is nodig om de molecuulformule te berekenen op basis van het massapercentage van elk element in een verbinding?  Flexibele microbatterijen voor wearables
Flexibele microbatterijen voor wearables Wat betekent een zwarte ring?
Wat betekent een zwarte ring?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

