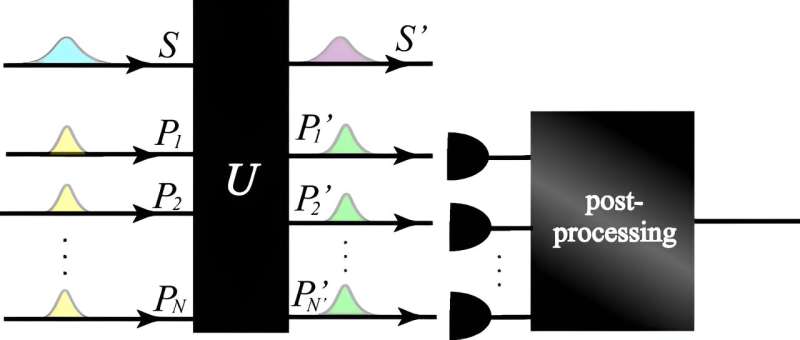
Een onderzoek gepubliceerd in het tijdschrift Physical Review Letters door onderzoekers in Japan lost een al lang bestaand probleem in de kwantumfysica op door het onzekerheidsprincipe te herdefiniëren.

Het onzekerheidsprincipe van Werner Heisenberg is een belangrijk en verrassend kenmerk van de kwantummechanica, en hij heeft daar zijn hooikoorts voor te danken. De jonge Duitse natuurkundige voelde zich in de zomer van 1925 ellendig in Berlijn en ging op vakantie op het afgelegen, rotsachtige eiland Helgoland, in de Noordzee voor de Noord-Duitse kust. Zijn allergieën verbeterden en hij kon zijn werk voortzetten in een poging de ingewikkeldheden van Bohrs atoommodel te begrijpen, waarbij hij tabellen ontwikkelde met interne atomaire eigenschappen, zoals energie, positie en momentum.

Toen hij terugkeerde naar Göttingen, besefte zijn adviseur, Max Born, dat deze tabellen elk in een matrix konden worden gevormd – in wezen een tweedimensionale waardentabel. Samen met de 22-jarige Pasqual Jordan verfijnden ze hun werk tot matrixmechanica – de eerste succesvolle theorie van de kwantummechanica – de natuurkundige wetten die kleine objecten zoals atomen en elektronen beschrijven.

Hoewel de matrixmechanica binnen enkele jaren vervangen zou zijn door de golffunctie van Schrödinger en zijn vergelijking, gaf het Heisenberg wel het inzicht om het onzekerheidsprincipe te formuleren:er is een grens aan hoe precies de locatie en het momentum van een kwantumsysteem, doorgaans een deeltje, kunnen zijn. gemeten.

De limiet van het product van de meetonzekerheden van de twee grootheden is h/4π, waarbij h de constante van Planck is, extreem klein maar toch niet nul. Kortom, je kunt niet zowel de positie als het momentum van een kwantumobject met willekeurige precisie meten; het meten van het ene met een hogere precisie betekent dat het andere alleen met een lagere precisie kan worden gemeten.

Stel dat we vanuit een fysiek perspectief de positie en het momentum van een elektron willen meten. Je moet op de een of andere manier licht op een systeem laten schijnen om de eigenschappen ervan te meten. Licht wordt gekwantiseerd als fotonen, die een niet-nul-energie hebben. Door een foton op het elektron te laten schijnen, wordt het elektron noodzakelijkerwijs uit zijn oorspronkelijke staat verstoord. In de kwantummechanica legt alleen al het meten een limiet op aan de nauwkeurigheid van de meting.

Soortgelijke onzekerheden gelden voor metingen van tijd en energie, en hoekpositie en impulsmoment, en in het algemeen twee variabelen die niet "pendelen" wanneer ze worden weergegeven als operatoren in de rigoureuze kwantummechanica.

Een paar decennia later werd het onzekerheidsprincipe door natuurkundigen Eugene Wigner, vervolgens Huzihiro Araki en Mutsuo M. Yanase verfijnd tot de stelling van Wigner-Araki-Yanase (WAY), die stelt dat voor twee waarneembare grootheden q en p, waarbij p behouden blijft ( zoals het momentum van een systeem), dan kan q, zelfs als p helemaal niet wordt gemeten, niet met willekeurige precisie worden gemeten.

"Als gevolg van de WAY-stelling kunnen we zien dat het (in zekere zin) onmogelijk is om de positie van het deeltje q te meten; het enige wat we kunnen meten is de positie ervan ten opzichte van het apparaat, q-Q", zegt wiskundige John Baez van het University of California, Riverside heeft geschreven, waarbij Q de positie van het meetapparaat is.

Maar de WAY-stelling was alleen van toepassing op grootheden zoals de spin van deeltjes, die alleen discrete en begrensde grootheden kunnen aannemen.

Nu hebben Yui Kuramochi van de Kyushu Universiteit en Hiroyasu Tajima van de Universiteit voor Elektrocommunicatie in Japan een al lang bestaand probleem opgelost door aan te tonen dat de WAY-stelling ook van toepassing is op waarneembare grootheden die continu (niet discreet) of onbegrensd zijn, zoals positie.

"Volgens het onzekerheidsprincipe kunnen positie en momentum niet tegelijkertijd nauwkeurig worden gemeten", aldus Kuramochi. "Ons resultaat geeft een extra beperking:zelfs alleen de positie zelf kan niet nauwkeurig worden gemeten, zolang we natuurlijke metingen gebruiken die voldoen aan het behoud van momentum." Hun bewijs onderzoekt een 'onbegrensde operator', fysieke grootheden die oneindig grote waarden kunnen aannemen.

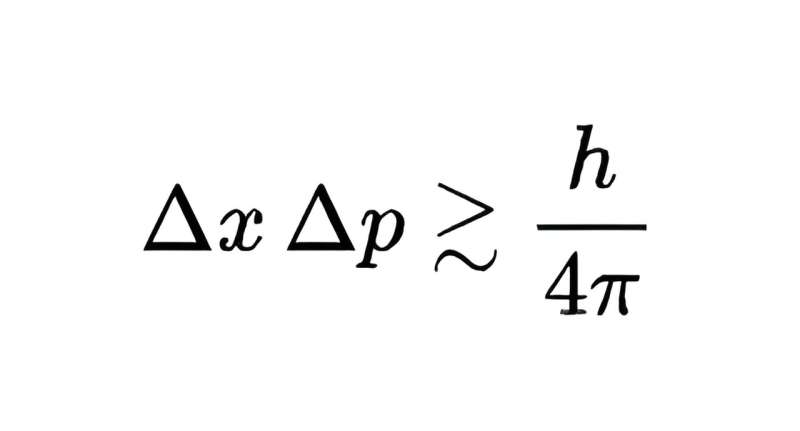
Strikt genomen vereist het resultaat een bepaalde voorwaarde die ten grondslag ligt aan de WAY-stelling, de zogenaamde Yanase-voorwaarde. Hoewel het zeer technisch is, bepaalt het in wezen de compatibiliteit van de onbegrensde variabele van het apparaat met de behouden hoeveelheid. De Yanase-voorwaarde lijkt, hoewel wiskundig, wenselijk voor toepassingen op fysieke systemen in de echte wereld.

‘Het WAY-theorema voorspelt dat onder een behoudswet een fysieke grootheid die niet met de behouden lading communiceert, niet zonder fouten kan worden gemeten’, vervolgt Kuramochi. "Dit komt overeen met een antwoord op een probleem dat al 60 jaar openstaat. Het nieuwe resultaat lost een decennia-oud probleem op over hoe dergelijke continue en onbegrensde waarneembare waarden moeten worden benaderd, vooral op gebieden als de kwantumoptica, waar de nieuwe stellinguitbreiding waarschijnlijk toepassingen zal vinden ."

De oorspronkelijke WAY-stelling verbiedt dat de meetfout nul is, maar het is een kwalitatieve stelling en specificeert niet de meetlimiet en zelfs niet of er een ondergrens groter dan nul is. Hetzelfde geldt voor deze WAY-stellinguitbreiding door Kuramochi en Tajima.

In hun artikel schrijven de auteurs dat het nog steeds een open vraag is of de oorspronkelijke WAY-stelling voor herhaalde metingen kan worden gegeneraliseerd zoals ze hebben gedaan, naar onbegrensde geconserveerde waarneembare waarden.

Het team suggereert nieuwe onderzoeksrichtingen naar uitbreidingen van de WAY-stelling en zou hun resultaten graag willen generaliseren naar staten met beperkte energie, aangezien hun huidige resultaten beperkt zijn tot staatsonafhankelijke gevallen en tot benaderende gevallen. Eén mogelijke toepassing is het stellen van grenzen aan de manier waarop transmissieprotocollen van kwantumnetwerken beter kunnen presteren dan klassieke limieten.

Meer informatie: Yui Kuramochi et al., Wigner-Araki-Yanase-stelling voor continue en onbegrensde geconserveerde observabelen, Physical Review Letters (2023). DOI:10.1103/PhysRevLett.131.210201

Journaalinformatie: Fysieke beoordelingsbrieven

© 2023 Science X Netwerk