
Wetenschap
Een nieuwe gerichte aanpak kan rommelige kwantum-scramblerproblemen helpen ontwarren
De wereld is een rommelige, lawaaierige plek en het vermogen om effectief te focussen is een waardevolle vaardigheid. Op een druk feest moeten bijvoorbeeld het gekletter van bestek, de gesprekken, de muziek, het krabben aan het label van je shirt en bijna al het andere naar de achtergrond verdwijnen, zodat je je kunt concentreren op het vinden van bekende gezichten of het geven van de persoon naast je. onverdeelde aandacht.
Op dezelfde manier zijn de natuur en experimenten vol afleidingen en verwaarloosbare interacties, dus moeten wetenschappers hun aandacht bewust richten op bronnen van nuttige informatie. De temperatuur van het drukbezochte feest is bijvoorbeeld het resultaat van de energie die door elk molecuul in de lucht wordt gedragen, de luchtstromen, de moleculen in de lucht die warmte opnemen als ze van de gasten afketsen en talloze andere interacties.
Maar als je alleen maar wilt meten hoe warm de kamer is, kun je beter een thermometer gebruiken die je de gemiddelde temperatuur van deeltjes in de buurt geeft, in plaats van te proberen alles wat er gebeurt vanaf atomair niveau te detecteren en te volgen. Een paar goedgekozen kenmerken, zoals temperatuur en druk, zijn vaak de sleutel tot het begrijpen van een complex fenomeen.
Het is vooral waardevol voor onderzoekers om hun aandacht te richten bij het werken aan de kwantumfysica. Wetenschappers hebben aangetoond dat de kwantummechanica kleine deeltjes en hun interacties nauwkeurig beschrijft, maar de details worden vaak overweldigend als onderzoekers kijken naar veel op elkaar inwerkende kwantumdeeltjes.
Het toepassen van de regels van de kwantumfysica op slechts enkele tientallen deeltjes is vaak meer dan welke natuurkundige dan ook – zelfs als hij een supercomputer gebruikt – kan bijhouden. Bij kwantumonderzoek moeten wetenschappers dus vaak essentiële kenmerken identificeren en bepalen hoe ze deze kunnen gebruiken om praktische inzichten te verkrijgen zonder te worden begraven in een lawine van details.
In een artikel gepubliceerd in het tijdschrift Physical Review Letters in januari 2024 identificeerden JQI Fellow Victor Galitski en JQI-afgestudeerde student Amit Vikram een nieuwe manier waarop onderzoekers nuttige inzichten kunnen verkrijgen in de manier waarop informatie die verband houdt met een configuratie van deeltjes verspreid raakt en in de loop van de tijd effectief verloren gaat. Hun techniek richt zich op één enkel kenmerk dat beschrijft hoe verschillende hoeveelheden energie kunnen worden vastgehouden door verschillende configuraties van een kwantumsysteem.
De aanpak biedt inzicht in hoe een verzameling kwantumdeeltjes kan evolueren zonder dat de onderzoekers hoeven te worstelen met de complexiteit van de interacties die ervoor zorgen dat het systeem in de loop van de tijd verandert.
Dit resultaat kwam voort uit een eerder project waarin het paar een definitie van chaos voor de kwantumwereld voorstelde. In dat project werkte het tweetal met een vergelijking die de relatie tussen energie en tijd beschrijft – de minder populaire neef van het onzekerheidsprincipe van Heisenberg voor positie en momentum.
Het onzekerheidsprincipe van Heisenberg betekent dat er altijd een afweging is tussen hoe nauwkeurig je tegelijkertijd de positie en het momentum van een kwantumdeeltje kunt kennen. De wisselwerking die wordt beschreven door de energie-tijd-onzekerheidsrelatie is niet zo netjes gedefinieerd als zijn neef, dus onderzoekers moeten de toepassing ervan afstemmen op verschillende contexten en voorzichtig zijn met hoe zij deze interpreteren. Maar over het algemeen betekent deze relatie dat het nauwkeuriger kennen van de energie van een kwantumtoestand de tijd doet toenemen die nodig is om de staat naar een nieuwe staat te laten overschakelen.
Toen Galitski en Vikram nadachten over de relatie tussen energie en tijd-onzekerheid, realiseerden ze zich dat deze zich op natuurlijke wijze leende voor het bestuderen van veranderingen in kwantumsystemen – zelfs die met veel deeltjes – zonder te verzanden in al te veel details. Met behulp van deze relatie ontwikkelde het tweetal een aanpak die slechts één kenmerk van een systeem gebruikt om te berekenen hoe snel de informatie in een initiële verzameling kwantumdeeltjes zich kan vermengen en verspreiden.
Het kenmerk waar ze hun methode omheen hebben gebouwd, wordt de spectrale vormfactor genoemd. Het beschrijft de energieën die de kwantumfysica toestaat dat een systeem vasthoudt en hoe vaak ze voorkomen – als een kaart die laat zien welke energieën gebruikelijk zijn en welke zeldzaam zijn voor een bepaald kwantumsysteem.
De contouren van de kaart zijn het resultaat van een bepalend kenmerk van de kwantumfysica:het feit dat kwantumdeeltjes alleen in bepaalde toestanden kunnen worden gevonden met verschillende – gekwantiseerde – energieën. En wanneer kwantumdeeltjes interageren, is de energie van de hele combinatie ook beperkt tot bepaalde discrete opties.
Voor de meeste kwantumsystemen zijn sommige van de toegestane energieën alleen mogelijk voor een enkele combinatie van de deeltjes, terwijl andere energieën het resultaat kunnen zijn van veel verschillende combinaties. De beschikbaarheid van de verschillende energieconfiguraties in een systeem heeft een diepgaande invloed op de resulterende fysica, waardoor de spectrale vormfactor een waardevol hulpmiddel is voor onderzoekers.
Galitski en Vikram hebben een formulering van de energie-tijd-onzekerheidsrelatie op maat gemaakt rond de spectrale vormfactor om hun methode te ontwikkelen. Deze aanpak is uiteraard van toepassing op de verspreiding van informatie, aangezien informatie en energie nauw verwant zijn in de kwantumfysica.
Terwijl ze deze verspreiding bestudeerden, richtten Galitski en Vikram hun aandacht op een open vraag in de natuurkunde, het snel-versleutelende vermoeden, dat tot doel heeft vast te stellen hoe lang het duurt voordat de organisatie van een initiële verzameling deeltjes is vervormd – om over de informatie ervan te beschikken. gemengd en verspreid onder alle op elkaar inwerkende deeltjes totdat het feitelijk onherstelbaar wordt.
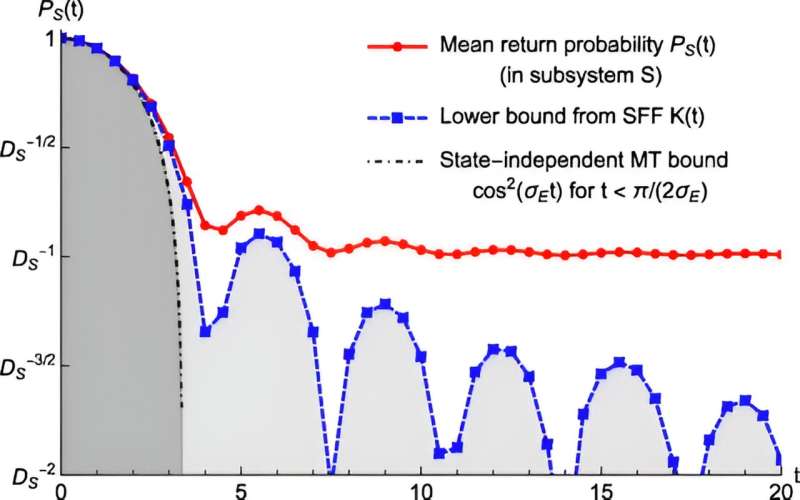
Het vermoeden gaat niet alleen over de snelste versleuteling die mogelijk is voor een enkel geval, maar gaat over hoe de tijd die de versleuteling in beslag neemt, verandert op basis van de omvang of complexiteit van het systeem.
Informatieverlies tijdens kwantumversleuteling is vergelijkbaar met het smelten van een ijssculptuur. Stel dat een beeldhouwer het woord ‘zwaan’ in ijs spelt en het vervolgens op een zonnige dag verstrooid in een bak met water laat liggen. In eerste instantie kunt u het woord in één oogopslag lezen. Later is de 's' op zijn kant gevallen en is de bovenkant van de 'a' eraf gevallen, waardoor het op een 'u' lijkt, maar je kunt nog steeds nauwkeurig raden wat het ooit heeft gespeld.
Maar op een gegeven moment is er gewoon een plas water. Het kan nog steeds koud zijn, wat erop wijst dat er recentelijk ijs heeft gelegen, maar er is geen praktische hoop om erachter te komen of het ijs een levensechte zwanensculptuur was, uitgehouwen in het woord 'zwaan', of gewoon een saai blok ijs.
Hoe lang het proces duurt, hangt af van zowel het ijs als de omgeving:misschien minuten voor een klein ijsblokje in een meer of een hele middag voor een zestig meter hoog middelpunt in een kleine plas.
De ijssculptuur lijkt op de initiële informatie die zich in een deel van de kwantumdeeltjes bevindt, en het omringende water bestaat uit alle andere kwantumdeeltjes waarmee ze kunnen interageren. Maar in tegenstelling tot ijs kan elk deeltje in de kwantumwereld tegelijkertijd meerdere toestanden bewonen, een kwantumsuperpositie genoemd, en onlosmakelijk met elkaar verbonden raken door kwantumverstrengeling, wat het afleiden van de oorspronkelijke toestand extra moeilijk maakt nadat deze de kans heeft gehad om te veranderen.
Om praktische redenen hebben Galitski en Vikram hun techniek zo ontworpen dat deze toepasbaar is op situaties waarin onderzoekers nooit de exacte toestanden kennen van alle op elkaar inwerkende kwantumdeeltjes.
Hun aanpak werkt voor een reeks gevallen, variërend van gevallen waarin informatie is opgeslagen in een klein deel van alle op elkaar inwerkende kwantumdeeltjes, tot gevallen waarin de informatie zich op een meerderheid van de deeltjes bevindt – van een ijsblokje in een meer tot een beeldhouwwerk in een plas. . Dit geeft de techniek een voordeel ten opzichte van eerdere benaderingen die alleen werken voor informatie die is opgeslagen op een paar van de originele deeltjes.
Met behulp van de nieuwe techniek kan het tweetal inzicht krijgen in hoe lang het duurt voordat een kwantumboodschap effectief wegsmelt voor een grote verscheidenheid aan kwantumsituaties. Zolang ze de spectrale vormfactor kennen, hoeven ze verder niets te weten.
"Het is altijd leuk om uitspraken te kunnen formuleren die zo weinig mogelijk veronderstellen, wat betekent dat ze zo algemeen mogelijk zijn binnen je basisaannames", zegt Vikram, de eerste auteur van het artikel. "De leuke kleine bonus op dit moment is dat de spectrale vormfactor een grootheid is die we in principe kunnen meten."
Het vermogen van onderzoekers om de spectrale vormfactor te meten zal hen in staat stellen de techniek te gebruiken, zelfs als veel details van het systeem een mysterie zijn. Als wetenschappers niet over voldoende details beschikken om de spectrale vormfactor wiskundig af te leiden of om een aangepaste beschrijving van de deeltjes en hun interacties op maat te maken, kan een gemeten spectrale vormfactor nog steeds waardevolle inzichten opleveren.
Als voorbeeld van het toepassen van de techniek keken Galitski en Vikram naar een kwantummodel van scrambling, het Sachdev-Ye-Kitaev (SYK) -model. Sommige onderzoekers denken dat er overeenkomsten kunnen zijn tussen het SYK-model en de manier waarop informatie wordt vervormd en verloren gaat als deze in een zwart gat valt.
Uit de resultaten van Galitski en Vikram bleek dat de tijd voor het versleutelen steeds langer werd naarmate ze naar steeds grotere aantallen deeltjes keken, in plaats van zich te vestigen in omstandigheden die zo snel mogelijk vervormden.
"Het duurt erg lang voordat grote verzamelingen deeltjes informatie verliezen in de rest van het systeem", zegt Vikram. ‘Dat is iets dat we op een heel eenvoudige manier kunnen bereiken zonder iets te weten over de structuur van het SYK-model, afgezien van het energiespectrum. En het houdt verband met dingen waar mensen over hebben nagedacht over vereenvoudigde modellen voor zwarte gaten. een zwart gat kan iets heel anders blijken te zijn dan niemand zich had kunnen voorstellen."
Galitski en Vikram hopen dat toekomstige experimenten hun resultaten zullen bevestigen, en ze zijn van plan te blijven zoeken naar meer manieren om een algemeen kwantumkenmerk te relateren aan de resulterende dynamiek zonder op veel specifieke details te vertrouwen.
Zij en hun collega's onderzoeken ook eigenschappen van de spectrale vormfactor waaraan elk systeem zou moeten voldoen, en werken aan het identificeren van beperkingen op het gebied van scrambling die universeel zijn voor alle kwantumsystemen.