Wetenschap
Nieuw raamwerk voor het classificeren van chaos en thermalisatie
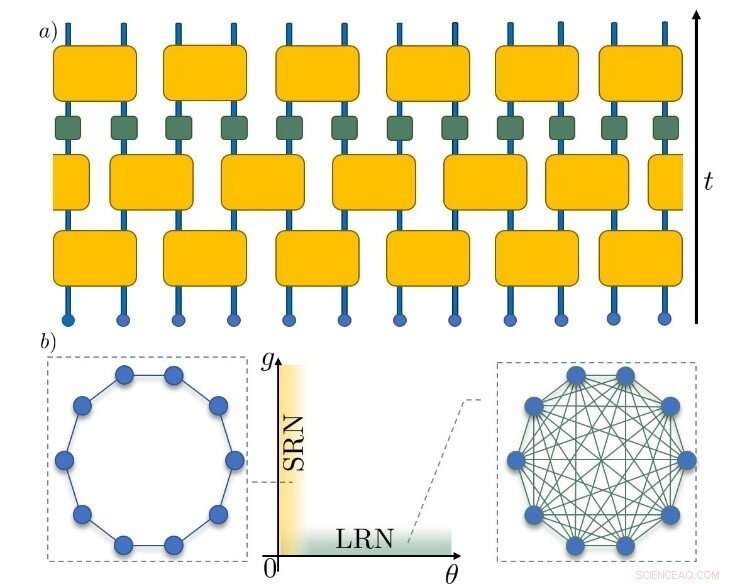
Figuur 1. Schematische weergave van het Unitary Circuit Map-model. (a) De zwarte pijl aan de rechterkant toont de richting van de tijd terwijl de deeltjes, weergegeven door kleine blauwe cirkels, evolueren. De gele vierkanten vertegenwoordigen de transformaties die de deeltjes koppelen. De groene vierkanten geven de chaos-inducerende niet-lineaire transformaties aan. (b) Afhankelijk van de geselecteerde parameters kan de koppeling tussen de deeltjes van korte (links) of lange (rechts) aard zijn. Dit heeft uiteindelijk invloed op de opkomende tijdschalen van chaotische dynamiek. Krediet:Instituut voor Basiswetenschappen
Een populair voorbeeld van chaotisch gedrag is het vlindereffect:een vlinder kan ergens in de Atlantische Oceaan met zijn vleugels klapperen en een tornado in Colorado veroorzaken. Deze opmerkelijke fabel illustreert hoe de extreme gevoeligheid van de dynamiek van chaotische systemen dramatisch verschillende resultaten kan opleveren ondanks kleine verschillen in de beginomstandigheden. De fundamentele natuurwetten die de dynamiek van fysieke systemen beheersen, zijn inherent niet-lineair, wat vaak leidt tot chaos en daaropvolgende thermalisatie.
Je kunt je echter afvragen waarom er geen ongebreidelde toename van tornado's in Colorado is, veroorzaakt door een enorme teleurstelling van vlinders in mondiale aangelegenheden, zoals bijvoorbeeld de opwarming van de aarde? Dit komt omdat fysieke dynamiek, hoewel chaotisch, in staat is om opmerkelijk stabiele toestanden aan te tonen. Een voorbeeld is de stabiliteit van ons zonnestelsel - het gehoorzaamt aan niet-lineaire wetten van de natuurkunde, die schijnbaar chaos in het systeem kunnen veroorzaken.
De reden voor deze stabiliteit berust op het feit dat zwak chaotische systemen een zeer geordende periodieke dynamiek kunnen vertonen die miljoenen jaren kan aanhouden. Deze ontdekking werd in de jaren vijftig gedaan door de grote wiskundigen Kolmogorov, Arnold en Moser. Hun ontdekking werkt echter alleen in het geval van systemen met een klein aantal op elkaar inwerkende elementen. Als het systeem veel samenstellende delen bevat, is het lot ervan niet zo goed begrepen.
Onderzoekers van het Center for Theoretical Physics of Complex Systems (PCS) binnen het Institute for Basic Science (IBS), Zuid-Korea, hebben onlangs een nieuw raamwerk geïntroduceerd voor het karakteriseren van zwak chaotische dynamiek in complexe systemen die een groot aantal samenstellende deeltjes bevatten. Om dit te bereiken, gebruikten ze een op kwantumcomputer gebaseerd model—Unitary Circuits Map—om chaos te simuleren.
Het onderzoeken van tijdschalen van chaotiek is een uitdagende taak, waarvoor efficiënte rekenmethoden nodig zijn. Het in deze studie geïmplementeerde Unitary Circuit Map-model beantwoordt aan deze eis. "Het model zorgt voor een efficiënte en foutloze voortplanting van toestanden in de tijd", legt Merab Malishava uit, "wat essentieel is voor het modelleren van extreem zwakke chaoticiteit in grote systemen. Dergelijke modellen werden eerder gebruikt om recordbrekende niet-lineaire evolutietijden te bereiken, wat was ook gedaan in onze groep."
Als gevolg hiervan waren ze in staat om de dynamiek binnen het systeem te classificeren door tijd- en lengteschalen te identificeren die naar voren komen als de thermalisatie dramatisch vertraagt. De onderzoekers ontdekten dat als de samenstellende delen op een langeafstandsnetwerk (LRN) zijn aangesloten (bijvoorbeeld op een alles-naar-alles), de thermalisatiedynamiek wordt gekenmerkt door één unieke tijdschaal, de Lyapunov-tijd. Als de koppeling echter van een korteafstandsnetwerk (SRN) is (bijvoorbeeld naaste buur), ontstaat er een extra lengteschaal die verband houdt met het langdurig bevriezen van grotere delen van het systeem met zeldzame chaotische spatten.
Meestal worden de onderzoeken naar dergelijke gevoelige dynamiek uitgevoerd met behulp van de technieken van het analyseren van het gedrag van waarneembare objecten. Deze technieken dateren uit de jaren vijftig, toen de eerste experimenten met chaoticiteit en thermalisatie werden uitgevoerd. De auteurs identificeerden een nieuwe analysemethode - door de Lyapunov-spectrumschaal te onderzoeken.
Merab Malishava zegt:"Vorige methoden kunnen leiden tot ambigue resultaten. Je kiest een waarneembare en merkt schijnbaar thermalisatie en denkt dat de dynamiek chaotisch is. Maar als een ander waarneembaar wordt bestudeerd, vanuit een ander perspectief, dan concludeer je dat het systeem bevroren is en niets verandert, wat betekent dat er geen thermalisatie is. Dit is de ambiguïteit die we hebben overwonnen. Het Lyapunov-spectrum is een reeks tijdschalen die de dynamiek volledig en volledig karakteriseren. En wat meer is, het is hetzelfde vanuit elk oogpunt! Uniek en ondubbelzinnig. "
De resultaten zijn niet alleen interessant vanuit een fundamenteel standpunt. Ze hebben ook het potentieel om licht te werpen op de realisaties van kwantumcomputers. Kwantumberekening vereist coherente dynamiek, wat geen thermalisatie betekent. In het huidige werk werd een dramatische vertraging van de thermische dynamiek bestudeerd met opkomende quasi-geconserveerde grootheden. Het kwantificeren van dit geval zou mogelijk fenomenen als lokalisatie van veel lichamen kunnen verklaren, wat een van de basisideeën is om thermalisatie in kwantumcomputers te voorkomen.
Een andere geweldige prestatie van het onderzoek heeft betrekking op de toepasbaarheid van de resultaten op een overgrote meerderheid van fysieke modellen, variërend van eenvoudige oscillatornetwerken tot complexe spinnetwerkdynamiek. Dr. Sergej Flach, de leider van de onderzoeksgroep en de directeur van PCS legt uit:"We hebben vijf jaar gewerkt aan de ontwikkeling van een raamwerk om zwak chaotische dynamiek in macroscopische systemen te classificeren, wat resulteerde in een reeks werken die het gebied aanzienlijk vooruitbrachten. We hebben nauw gerichte case-by-case studies terzijde geschoven ten gunste van het bevorderen van een conceptuele benadering die betrouwbaar en relateerbaar is in een groot aantal fysieke realisaties. Dit specifieke werk is een zeer belangrijke bouwsteen in het bovengenoemde kader. We ontdekten dat een traditionele manier van kijken is soms niet de meest informatieve en bood een nieuwe alternatieve benadering. Ons werk stopt hier geenszins, omdat we uitkijken naar het bevorderen van de wetenschap met meer baanbrekende ideeën."
Dit onderzoek is onlangs gepubliceerd in Physical Review Letters. + Verder verkennen
Bevriezing bij verhitting:Vorming van dynamisch glas
 Onderzoekers rapporteren nieuwe techniek voor het ontdooien van oppervlakken
Onderzoekers rapporteren nieuwe techniek voor het ontdooien van oppervlakken Plastic dat de planeet redt? Nieuwe hars voor startups helpt de industrie groen te worden
Plastic dat de planeet redt? Nieuwe hars voor startups helpt de industrie groen te worden Welke rol speelt chlorofyl in fotosynthese?
Welke rol speelt chlorofyl in fotosynthese?  Borstimplantaten markeren met tomaten-DNA om namaak te voorkomen
Borstimplantaten markeren met tomaten-DNA om namaak te voorkomen Hoe stabiliseert water de temperatuur?
Hoe stabiliseert water de temperatuur?
 Vogels die van glimmende dingen houden
Vogels die van glimmende dingen houden Een nieuwe kijk op (afval)water en milieubehoud
Een nieuwe kijk op (afval)water en milieubehoud Nieuw onderzoek snijdt door de waas rond rookvrije tabaksproducten
Nieuw onderzoek snijdt door de waas rond rookvrije tabaksproducten Nieuwe studie zegt dat wetenschappelijke basis voor EPA's Endangerment Finding sterker is dan ooit
Nieuwe studie zegt dat wetenschappelijke basis voor EPA's Endangerment Finding sterker is dan ooit NASA ziet extra-tropische storm Saola langs Japan bewegen
NASA ziet extra-tropische storm Saola langs Japan bewegen
Hoofdlijnen
- Genezing van verbrande poten met vissenhuid
- Welke vormen over het midden van een cel nabij het einde van Telophase?
- Fun Biology Presentatie Onderwerpen
- Honingbijen ultra-verbonden door hun microbioom
- Drie voorbeelden van protisten met wetenschappelijke namen
- Van stroper tot boswachter:de Siberische tijgers van China redden
- Namen van de Enzymen in de Mond & Esophagus
- Hoe komen de spermacellen in een stuifmeelkorrel aan bij de eicelklus in een plant-ovule?
- Japanse walvisjagers naar Antarctica
 Gezonde bodem verhoogt het gewicht van de dieren
Gezonde bodem verhoogt het gewicht van de dieren Het komt allemaal neer op ruwheid
Het komt allemaal neer op ruwheid Astronomen onderzoeken planetaire nevel NGC 6302 met Hubble
Astronomen onderzoeken planetaire nevel NGC 6302 met Hubble Hoe Monomials en binomials af te trekken
Hoe Monomials en binomials af te trekken  Testlocatie voor door ESA gesteunde luchtademende motor
Testlocatie voor door ESA gesteunde luchtademende motor Onderzoekers ontwikkelen techniek die explosieven kan detecteren, gevaarlijke gassen snel en op afstand
Onderzoekers ontwikkelen techniek die explosieven kan detecteren, gevaarlijke gassen snel en op afstand Vliegen door de veiligere lucht
Vliegen door de veiligere lucht Ultra-diffuus sterrenstelsel F8D1 heeft een gigantische getijdenstaart, waarnemingen vinden
Ultra-diffuus sterrenstelsel F8D1 heeft een gigantische getijdenstaart, waarnemingen vinden
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com