
Wetenschap
Gelokaliseerde orbitale schaalcorrectiefunctie die DFT naar een nieuw niveau van nauwkeurigheid brengt
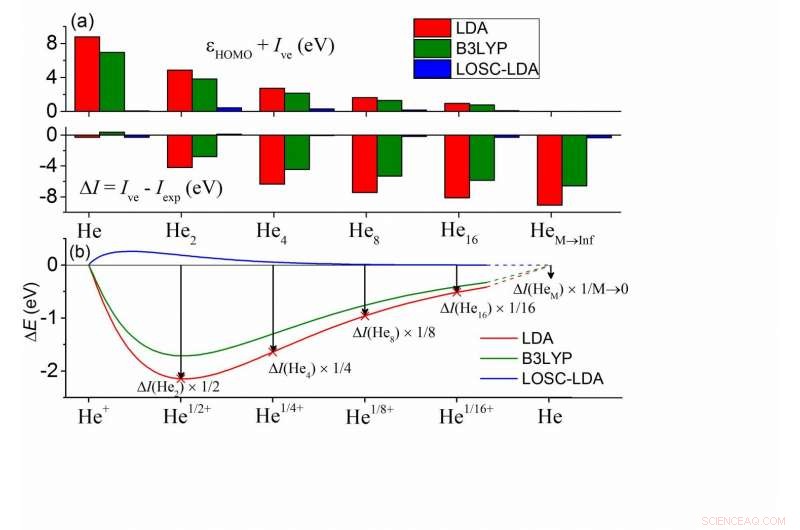
(a) Afwijkingen tussen de berekende ?HOMO en -Ive en tussen Ive en Iexp voor een reeks HeM-clusters. In elke cluster zijn alle He-atomen chemisch equivalent. De dichtstbijzijnde naburige atomen zijn gescheiden door 10Å, en de Iexp van HeM wordt goed benaderd door Iexp van een He-atoom. (b) Berekende totale energie-afwijking van de lineariteitsvoorwaarde van een fractioneel geladen He-atoom als functie van de fractionele lading δ. Hier ΔE(Heδ+) =E(Heδ+)-δE(He+)-(1-δ)E(He), en de δ-waarden zijn in de figuur geschaald voor een directe vergelijking met (a). Krediet:©Science China Press
De dichtheidsfunctionaaltheorie van Kohn-Sham is een van de meest succesvolle theorieën in de chemie. Het is formeel streng; zijn relatief lage rekenkosten en concurrerende nauwkeurigheid in kleine en middelgrote systemen maken het een van de meest populaire methoden in elektronische structuurberekeningen, en misschien wel de enige keuze voor het modelleren van kwantumeffecten van elektronen in grote chemische en biologische systemen. Hoe dan ook, de exacte functionele is niet expliciet bekend en de state-of-the-art densiteit functionele benaderingen (DFA's) lijden aan systematische fouten. Een van de dominante fouten in DFA's is de delokalisatiefout, die alomtegenwoordig is en zich op verschillende manieren manifesteert. Dit is al tientallen jaren een uitdagend open probleem. Onlangs, Chen Li, Neil Qiang Su en Weitao Yang van Duke University en Xiao Zheng van de University of Science and Technology of China ontwikkelden een nieuw gelokaliseerd orbital scaling correction (LOSC)-raamwerk dat de systematische eliminatie van de delokalisatiefout aantoont.
De belangrijkste gevolgen van delokalisatiefouten in DFA's kunnen worden onderverdeeld in twee aspecten:(1) Kohn-Sham (KS) orbitale energiefout en (2) totale energiefout. De delokalisatiefout leidt tot belangrijke mislukkingen in praktische toepassingen zoals de onfysische onderschatting van bandhiaten, de buitensporig gedelokaliseerde elektronenverdelingen en verkeerde ladingsoverdrachten. Wat deze twee aspecten van fouten betreft, beide manifesteren zich op een grootteafhankelijke manier. Vooral, onder de KS-orbitale energieën, de hoogste bezette moleculaire orbitale (HOMO) energie, HOMO, wordt verondersteld overeen te komen met de (negatieve) verticale ionisatiepotentiaal (-Ive), zoals vereist door de exacte functionele. Verder, de Ive zoals berekend door DFA's worden verondersteld overeen te komen met de experimentele waarde, Iexp.
Voor veelgebruikte DFA's, aan de twee voorwaarden is niet voldaan. Zoals blijkt uit de heliumclusterberekeningen in de subfiguur (a), de HOMO-energie door de lokale dichtheidsbenadering (LDA) toont een positieve fout in vergelijking met -Ive terwijl Ive een negatieve fout vertoont, en de twee fouten worden op een grootteafhankelijke manier weergegeven, wat suggereert dat de delokalisatiefout van DFA's op de een of andere manier moet verschijnen, of allebei, terwijl de som van de grootheden ongewijzigd blijft. Bovendien, dit komt veel voor in allerlei DFA's, inclusief de meest populaire B3LYP-functioneel, zoals weergegeven in het groen.
Om deze fouten te begrijpen, scheikundigen kunnen ze in kaart brengen in de fouten van een fractioneel geladen He-atoom, zoals geïllustreerd in de subfiguur (b). De fractionele systeemenergieën worden verondersteld lineair te schalen met het fractionele elektronengetal n (0?n <1) voor de exacte functie. Getoond in subfiguur (b) is de energie-afwijking van de lineariteitsvoorwaarde voor een enkel He-atoom, waar de fractionele systeemenergieën worden onderschat, definieert dit de delokalisatiefout. Bovendien, de fractionele ladingsfout in (b) komt 1-1 overeen met de totale energiefout ΔI =Ive - Iexp. In de limiet van M gaat naar oneindig, kan men afleiden dat ΔI overeenkomt met de hellingsfout van de E(N)-curve bij het gehele getal, wat precies de HOMO-energiefout is van een enkel He-atoom. Daarom, alle fouten zijn met elkaar verbonden. Het is dus mogelijk om delokalisatiefout systematisch te elimineren door (1) de fouten in (b) te verwijderen en (2) te garanderen dat de fout in alle systemen op een consistente manier wordt verwijderd.
In het huidige werk van LOSC, de auteurs bedachten nieuwe lokale variabelen, orbitallets genoemd, dit zijn gelokaliseerde orbitalen (LO's) die lokaliteit bereiken in zowel ruimtelijke als energieruimten. Door deze orbitallets, ze waren in staat om de elektronendichtheid en KS-dichtheidsmatrix uit te drukken in de lokale weergave, waar de lokale bezettingsmatrix die bestaat uit fractionele getallen op natuurlijke wijze ontstaat. Daarom, deze lokale variabelen zijn in staat om lokale fractionele informatie nauwkeurig en volledig vast te leggen in de orbitale ruimte, en dienen als de perfecte bouwstenen voor de LOSC-functionaliteit. Verder, door de termen in de GSC- en LSC-functionaliteiten te herschrijven in termen van formules voor krommingscorrectie en analogie te maken met de LOSC, ze introduceerden een lokale krommingsmatrix, waarvan de elementen zijn ontworpen als een functie van de orbitallets, één-op-één correspondentie met de lokale bezettingsmatrix. Eindelijk, de LOSC-formule is geschreven als een expliciete en elegante uitdrukking over de bovenliggende functionele in termen van deze twee matrices.
De LOSC bereikt alle gewenste functies. In de bovenstaande figuur is de LOSC-LDA-fouten zijn in wezen verwaarloosbaar klein, om de geldigheid en consistentie van de correctie aan te geven. Deze zijn ook gevalideerd door de sterk verbeterde dissociatiecurven van diatomische moleculaire kationen, variërend van H2+, hij2+, water dimeer kation en benzeen dimeer kation. de HOMO, LUMO-energiefouten zijn aanzienlijk verminderd en de goede prestaties blijven behouden naarmate de systeemomvang groeit. Dit is aangetoond door testen op polyaceen- en trans-polyacetyleenoligomeren. Verder, de LOSC is in staat om de juiste elektronendichtheid te verkrijgen wanneer de ouder-DFA's het kwalitatief verkeerd maken, zoals blijkt uit het voorbeeld van een gesolvateerd chlooranion wanneer beroofd van een elektron.
De prestaties van LOSC tonen dus de belofte van het systematisch elimineren van delokalisatiefouten binnen de KS-dichtheidsfunctionaliteiten. Het is vermeldenswaard dat, in tegenstelling tot het traditionele paradigma van het ontwerpen van functionalen met behulp van de dichtheid, de dichtheidsgradiënten, de kinetische energiedichtheid, enzovoort., het LOSC-raamwerk omvat volledig nieuwe ingrediënten, de orbitallets, die zelf impliciete functionalen zijn van de KS-dichtheidsmatrix, en demonstreerden hun unieke vermogen om langdurige problemen in verband met traditionele DFA's aan te pakken. Dit weerspiegelt een paradigmaverandering in het ontwerpen van functionalen, en verbreedt de weg enorm in de zoektocht naar het exacte functionele in de eigen leefruimte. In deze betekenis, LOSC heeft de trend ingeluid in het ontwikkelen van een nieuwe generatie dichtheidsfunctionele benaderingen, het bevorderen van de dichtheidsfunctionaaltheorie naar een nieuw niveau van nauwkeurigheid.
 Soorten waterplanten en dieren in de rivier de Mississippi
Soorten waterplanten en dieren in de rivier de Mississippi  Bomen in de uiterwaarden van de Amazone stoten evenveel methaan uit als alle oceanen van de aarde samen
Bomen in de uiterwaarden van de Amazone stoten evenveel methaan uit als alle oceanen van de aarde samen Kunnen verzekeringspremies ervoor zorgen dat we klimaatverandering heelhuids doorkomen?
Kunnen verzekeringspremies ervoor zorgen dat we klimaatverandering heelhuids doorkomen? Dit enzym stelde het leven in staat een vijandige aarde te veroveren
Dit enzym stelde het leven in staat een vijandige aarde te veroveren Voormalige kerncentrale in Colorado open voor publiek als toevluchtsoord voor wilde dieren
Voormalige kerncentrale in Colorado open voor publiek als toevluchtsoord voor wilde dieren
Hoofdlijnen
- Wat beïnvloedt een Trait Expression de meeste, genetica of de omgeving?
- Een omkeerbare hoofdschakelaar ontdekken voor ontwikkeling
- Octopussen gestrand op het strand van Wales - hier zijn de wetenschappelijke theorieën waarom
- Bioom: definitie, types, kenmerken en voorbeelden
- De machtige Banyan-boom kan eeuwenlang lopen en leven
- Onderzoek suggereert dat gorilla's spontaan voedselreinigingsgedrag kunnen ontwikkelen
- Mysterieuze nieuwe DNA-structuur gevonden in levende menselijke cellen
- The Differences Between Clams & Scallops
- Wetenschappers volgen haaien die DNA-fragmenten uit de zee plukken
- Schoenkoordtheorie:de wetenschap laat zien waarom schoenveters loskomen

- Nieuwe techniek onthult de ingewikkelde schoonheid van een gebarsten glas

- Gevangen elektronen prikkelen kernen naar hogere energietoestanden

- Fragmenten van energie - geen golven of deeltjes - kunnen de fundamentele bouwstenen van het universum zijn

- Hoe worden elementen gevormd in sterren?

 Nanodwergen worden tumormoordenaars
Nanodwergen worden tumormoordenaars Donkere luchtverordening om de lichtvervuiling van Pittsburgh te dimmen
Donkere luchtverordening om de lichtvervuiling van Pittsburgh te dimmen Hoe is een schroef als een hellend vlak?
Hoe is een schroef als een hellend vlak?  Wetenschappers verklaren vorming van maanstofwolken
Wetenschappers verklaren vorming van maanstofwolken Gemeenschappelijke Huisspinnen in Wisconsin
Gemeenschappelijke Huisspinnen in Wisconsin  Bedreigde planten in Maleisië
Bedreigde planten in Maleisië De uitdagingen van een buitenaards ruimtevluchtprogramma:ontsnappen aan superaarde en rode dwergsterren
De uitdagingen van een buitenaards ruimtevluchtprogramma:ontsnappen aan superaarde en rode dwergsterren Wet op op afbeeldingen gebaseerd seksueel misbruik en online verwijdering niet geschikt voor het beoogde doel
Wet op op afbeeldingen gebaseerd seksueel misbruik en online verwijdering niet geschikt voor het beoogde doel
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

