
Wetenschap
De straal van een niobiumatoom heeft een dichtheid van 8,57 en kristalliseert met de op het lichaam gecentreerde kubieke eenheidscel?
$$V=a^3$$
Waarbij 'a' de lengte van de rand van de kubus is.
Het volume van één niobiumatoom is:
$$V_{Nb}=(4/3)\pi r^3$$
Omdat er twee atomen per eenheidscel zijn, is het volume van twee niobiumatomen:
$$2V_{Nb}=(8/3)\pi r^3$$
Als we deze twee volumes gelijk aan elkaar stellen, krijgen we:
$$a^3=(8/3)\pi r^3$$
Als we 'r' oplossen, krijgen we:
$$r=\sqrt[3]{\frac{3a^3}{8\pi}}$$
De dichtheid van Niobium wordt gegeven door:
$$\rho=\frac{2M}{a^3N_A}$$
Waar M de molaire massa van Niobium is (92,91 g/mol), $N_A$ het getal van Avogadro is (6,022 x 10^23 atomen/mol), en 'a' de lengte van de rand van de kubus is.
Als we 'a' oplossen, krijgen we:
$$a=\sqrt[3]{\frac{2M}{\rho N_A}}$$
Als we deze uitdrukking voor 'a' vervangen door de vergelijking voor 'r', krijgen we:
$$r=\sqrt[3]{\frac{3(2M/\rho N_A)^3}{8\pi}}$$
Als we de waarden voor M, $\rho$ en $N_A$ invoeren, krijgen we:
$$r=\sqrt[3]{\frac{3(2\times92.91\text{ g/mol}/8.57\text{ g/cm}^3\times6.022\times10^{23}\text { atomen/mol})^3}{8\pi}}$$
$$r=1,43\times10^{-8}\text{ cm}$$
Daarom is de straal van een niobiumatoom $$1,43\times10^{-8}\text{ cm}$$.
 Rode vloed blijft zich verspreiden rond het zuidwesten van Florida
Rode vloed blijft zich verspreiden rond het zuidwesten van Florida Fysieke kenmerken van de Northeast
Fysieke kenmerken van de Northeast We kunnen luchthavens niet uitbreiden nadat we een klimaatnoodtoestand hebben uitgeroepen - laten we in plaats daarvan overschakelen op koolstofarm transport
We kunnen luchthavens niet uitbreiden nadat we een klimaatnoodtoestand hebben uitgeroepen - laten we in plaats daarvan overschakelen op koolstofarm transport De verschillen tussen dieren en insecten
De verschillen tussen dieren en insecten  Extreme zeespiegels zullen naar verwachting langs de wereldwijde kustlijnen stijgen
Extreme zeespiegels zullen naar verwachting langs de wereldwijde kustlijnen stijgen
Hoofdlijnen
- Hoe boeren en technologie samenwerken om gewassen beter te testen
- Namen van de structurele componenten van het menselijk hart
- Studie vindt variatie binnen soorten een cruciaal aspect van biodiversiteit
- Wat is het gebruik van computers in de biologie?
- Jackfruit uit de schappen laten springen
- Waarom kunnen de onderzoeken van Robert Hooke en Anton van Leeuwenhoek worden beschouwd als een begin van microscopiemicrobiologie?
- Plantaanpassingen: woestijn, tropisch regenwoud, toendra
- De controverse over Imane Khelif laat zien hoe sekstesten in de vrouwensport toezichthouders voor een onmogelijke opgave plaatsen
- Wetenschappers koppelen eicelspecifieke histon H1FOO aan een betere iPS-celgeneratie
- Speekseltest voor cannabis kan ooit helpen bij het identificeren van gehandicapte bestuurders

- Nieuwe grieptest gemakkelijk als ademen, met sneller resultaat

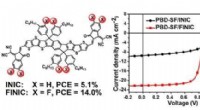
- Onderzoekers ontwikkelen elektronenacceptor met gefuseerde ring met 3D-exciton en ladingstransport
- Nieuwe fotonische vloeibare kristallen kunnen leiden tot displays van de volgende generatie

- Miniproteïnen die tweeledige aanvallen op virale eiwitten kunnen lanceren

 Gecombineerd team van natuurkundigen en biologen bouwen de ziekte van Lyme detector met behulp van koolstof nanobuis sensor
Gecombineerd team van natuurkundigen en biologen bouwen de ziekte van Lyme detector met behulp van koolstof nanobuis sensor Waar is de zwaartekrachtlijn van het menselijk lichaam?
Waar is de zwaartekrachtlijn van het menselijk lichaam?  Tesla onthult Model Y SUV, uitbreiden naar populair segment
Tesla onthult Model Y SUV, uitbreiden naar populair segment Oud DNA brengt ons dichter bij het ontsluiten van de geheimen van hoe de moderne mens is geëvolueerd
Oud DNA brengt ons dichter bij het ontsluiten van de geheimen van hoe de moderne mens is geëvolueerd  Deens rechtssysteem opgeschrikt door gebrekkig bewijs van telefoonlocatie
Deens rechtssysteem opgeschrikt door gebrekkig bewijs van telefoonlocatie De auto is koning in L.A. County, ondanks de groeiende mogelijkheden voor openbaar vervoer
De auto is koning in L.A. County, ondanks de groeiende mogelijkheden voor openbaar vervoer De dag breekt aan in een vierdaagse werkweek
De dag breekt aan in een vierdaagse werkweek Innovatie is wijdverbreid in landelijke gebieden, niet alleen steden
Innovatie is wijdverbreid in landelijke gebieden, niet alleen steden
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

