
Wetenschap
Een tango met verwarde polymeren

Chris Soteros. Krediet:Universiteit van Saskatchewan
Terwijl statistici worden gedreven door problemen uit de echte wereld, U of S wiskundeprofessor Chris Soteros wordt gemotiveerd door het meer esoterische gedrag van moleculen met een lange keten, zoals polymeren en DNA, en de wiskundige problemen die ze opleveren.
Haar werk omvat het analyseren van het vouw- en 'verpakkingsgedrag' van deze moleculen. Aangezien in elke cel van ons lichaam twee meter DNA is gevouwen, het bestuderen van het gedrag is inderdaad ontmoedigend.
Om het probleem te helpen oplossen, Soteros vereenvoudigt en simuleert deze moleculen op een driedimensionaal rooster, gebruikt vervolgens wiskundige hulpmiddelen zoals willekeurige en zelfvermijdende wandelingen om hun gedrag te modelleren.
Het sporadische pad van een willekeurige wandeling wordt vaak omschreven als "een dronkaards wandeling naar huis, " en wordt gebruikt om willekeurige bewegingen in grote datasets te modelleren - van beursschommelingen tot deeltjesfysica. Een zelfvermijdende wandeling is een willekeurige wandeling die niet hetzelfde pad kan kruisen of stappen kan volgen. Aangezien geen twee atomen dezelfde ruimte kunnen innemen, in drie dimensies is het een ideaal hulpmiddel om polymeergedrag te modelleren.
Om het gedrag van polymeren te bestuderen, Soteros modelleert een polymeeroplossing door een roosterloop te gebruiken om het polymeer weer te geven en de lege ruimtes eromheen om de oplosmiddelmoleculen van de oplossing weer te geven.
In experimentele oplossing bij hoge temperaturen, het polymeer gedraagt zich als een zichzelf vermijdende wandeling. "Bij deze temperaturen het polymeer geeft er de voorkeur aan dicht bij de oplosmiddelmoleculen te zijn, maar als je de temperatuur verlaagt, het polymeer staat het liefst dichter bij zichzelf, ", legt Soteros uit.
Verrassend genoeg, bij een bepaalde lagere temperatuur gedraagt het polymeer zich als een random walk, en onder die temperatuur vindt een "instorting"-overgang plaats, en het polymeer vouwt zichzelf in.
"Het was pas in de late jaren '70 dat de instortingsovergang werd waargenomen in het laboratorium, en je moest een zeer groot molecuul in een zeer verdunde oplossing hebben om de overgang te zien, " zegt Soteros. "Dit is een voorbeeld van wiskunde die een gedrag voorspelt voordat het door experimenten werd bevestigd."
Soms worden theorieën andersom ontdekt. Oud-student Michael Szafron (MSc'00, BEd'09, Ph.D.'09) - nu assistent-professor aan de School of Public Health - kwam naar Soteros met een complex probleem. Lange strengen DNA kunnen in de knoop raken als ze in de celkern worden verpakt, maar om succesvol te repliceren, DNA moet worden ontknoopt. Enzymen die type II-topoisomerasen worden genoemd, voeren de noodzakelijke ontwarring uit door één streng DNA te knippen, de andere streng door de breuk halen en vervolgens de uiteinden van de gebroken streng weer vastmaken. Hoe werkt deze verrassende oplossing zo goed, en hoe kan het wiskundig worden gemodelleerd?
Het helpt om je een lange ketting voor te stellen met een knoop; het losmaken van de gesp helpt om de knoop te ontwarren. "Het probleem is dat een sluiting van een ketting ver weg kan zijn van waar de knoop zit, dus het zou moeilijk zijn om het door te trekken, ", zegt Soteros. Toch lijken deze enzymen precies te weten waar ze het DNA moeten knippen.
Door het basisgedrag van zeer grote moleculen in oplossing te modelleren, Soteros bouwt wiskundig bewijs om te begrijpen hoe deze enzymen zo efficiënt werken - en hoe ze kunnen worden gebruikt om nieuwe antibiotica en geneesmiddelen tegen kanker te ontwikkelen.
 Mexico zet zich schrap voor mogelijk catastrofale orkaan Willa
Mexico zet zich schrap voor mogelijk catastrofale orkaan Willa Bosbrand in Oregon verbrandt gebied bijna zo groot als Los Angeles
Bosbrand in Oregon verbrandt gebied bijna zo groot als Los Angeles Onderzoek suggereert dat vlees- en zuivelindustrie op schema ligt om oliemaatschappijen te overtreffen als grootste uitstoters van broeikasgassen
Onderzoek suggereert dat vlees- en zuivelindustrie op schema ligt om oliemaatschappijen te overtreffen als grootste uitstoters van broeikasgassen Watergovernance:kan minder soms meer zijn?
Watergovernance:kan minder soms meer zijn? Kan een verenigd pad voor ontwikkeling en behoud leiden tot een betere toekomst?
Kan een verenigd pad voor ontwikkeling en behoud leiden tot een betere toekomst?
Hoofdlijnen
- Wetenschappers presenteren een nieuwe methode om elk eiwit in elk soort cel direct en snel te vernietigen
- Twee neuropeptiden in zebravissen geven aanwijzingen voor de complexe neurale mechanismen die ten grondslag liggen aan slaap
- Hoe het boren naar olie in het Arctic National Wildlife Refuge van invloed kan zijn op dieren in het wild
- Interferentie berekenen
- Hoe werkt het skelet met het ademhalingssysteem?
- Hoe maak je een celmodel van een Amoeba
- Wetenschappers werken aan een omkeerbare vorm van genbewerking
- Knollen in de problemen
- Wat worden clusters van cellichamen genoemd?
- Neerslag titratie technieken

- Atmosferische koolstof omzetten in industrieel bruikbare materialen

- Hoogenergetisch vormgeheugenpolymeer kan op een dag robots helpen hun spieren te buigen
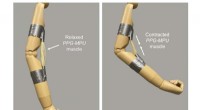
- Enzymconformatie beïnvloedt de prestaties van lipase-aangedreven nanomotoren
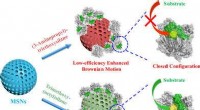
- Stal, zelfverstorende microbellen als intraveneuze zuurstofdragers

 De gemiddelde lengte van Mahi Mahi
De gemiddelde lengte van Mahi Mahi  Nationale leiders bezoeken waarvan is aangetoond dat ze de publieke opinie in gastlanden beïnvloeden
Nationale leiders bezoeken waarvan is aangetoond dat ze de publieke opinie in gastlanden beïnvloeden Onderzoek werpt nieuw licht op vroege turquoise mijnbouw in het zuidwesten
Onderzoek werpt nieuw licht op vroege turquoise mijnbouw in het zuidwesten Dag
Dag  Zacht en bolvormig:onderzoekers bestuderen dynamiek van druppelimpact
Zacht en bolvormig:onderzoekers bestuderen dynamiek van druppelimpact Welke wapens werden tijdens de koloniale dagen van North Carolina gebruikt?
Welke wapens werden tijdens de koloniale dagen van North Carolina gebruikt?  Nanosponzen nemen keer op keer olie op
Nanosponzen nemen keer op keer olie op Een consensusdocument over de stand van de wetenschap ter bestrijding van desinformatie
Een consensusdocument over de stand van de wetenschap ter bestrijding van desinformatie
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | German | Dutch | Danish | Norway | Swedish |

-
Wetenschap © https://nl.scienceaq.com

