
Wetenschap
Diep leren vanuit een dynamisch oogpunt
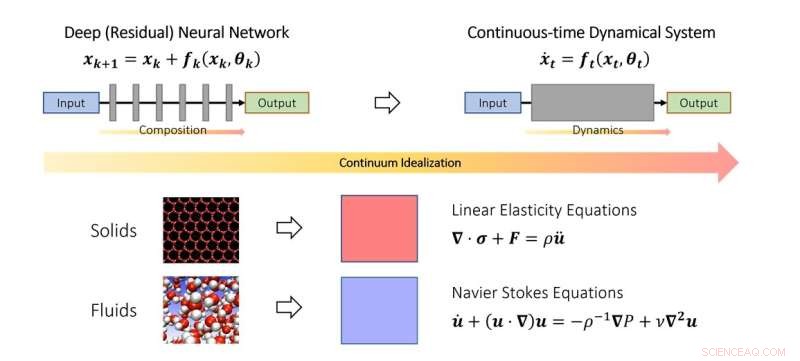
Het continue gezichtspunt van diep leren. Net zoals wetenschappers vaste- en vloeistofmechanica bestuderen in de continuümlimiet, kan men diepe neurale netwerken ook idealiseren als een discretisatie van een continu dynamisch systeem. In het schema vertegenwoordigt de fictieve tijdparameter een continu analoog van lagen en de dynamica modelleert de laagstapeling. Krediet:Qianxiao Li
NUS-wiskundigen hebben een nieuw theoretisch raamwerk ontwikkeld op basis van dynamische systemen om te begrijpen wanneer en hoe een diep neuraal netwerk willekeurige relaties kan leren.
Ondanks het grote succes in de praktijk, blijft het begrijpen van de theoretische principes van deep learning een uitdagende taak. Een van de meest fundamentele vragen is:kunnen diepe neurale netwerken willekeurige input-outputrelaties leren (in de wiskunde worden dit functies genoemd), en verschilt de manier waarop ze dit bereiken van traditionele methodologieën?
Om deze vraag te begrijpen, is het noodzakelijk om na te denken over wat er precies nieuw is in diepe neurale netwerken in vergelijking met traditionele paradigma's voor functiebenadering. Klassieke Fourierreeksen benadert bijvoorbeeld gecompliceerde functies als een gewogen som van eenvoudigere functies, zoals sinussen en cosinussen. Diepe neurale netwerken werken heel anders. In plaats van gewogen sommen bouwen ze complexe functies uit het herhaaldelijk opstapelen van eenvoudige functies (lagen). Dit wordt in de wiskunde ook wel functiesamenstelling genoemd. De hamvraag is hoe ingewikkelde functies kunnen worden opgebouwd uit eenvoudige door ze op elkaar te stapelen. Het blijkt dat dit een vrij nieuw probleem is in de tak van de wiskunde die bekend staat als de benaderingstheorie.
In deze studie gepubliceerd in het Journal of the European Mathematical Society , ontwikkelden assistent-professor Qianxiao LI van de afdeling Wiskunde, National University of Singapore en zijn medewerkers een nieuwe theorie over de benaderingsmogelijkheden van functiesamenstelling. Een interessante observatie is dat hoewel functiesamenstelling een uitdaging is om in de praktijk te analyseren vanwege de discrete en niet-lineaire structuur, dit niet de eerste keer is dat er dergelijke problemen zijn.
In de studie van de beweging van vaste stoffen en vloeistoffen worden ze vaak geïdealiseerd als een continuüm van deeltjes, die voldoen aan enkele continue vergelijkingen (gewone of partiële differentiaalvergelijkingen). Hierdoor kan de moeilijkheid van het modelleren van dergelijke systemen op het discrete, atomaire niveau worden omzeild. In plaats daarvan werden continuümvergelijkingen afgeleid die hun gedrag op macroscopisch niveau modelleren.
De kerngedachte in de studie is dat dit concept kan worden uitgebreid tot diepe neurale netwerken, door de gelaagde structuur te idealiseren als een continu dynamisch systeem. Dit verbindt deep learning met de tak van de wiskunde die bekend staat als dynamische systemen. Dergelijke verbindingen maken de ontwikkeling mogelijk van nieuwe hulpmiddelen om de wiskunde van diep leren te begrijpen, inclusief een algemene karakterisering van wanneer het inderdaad willekeurige relaties kan benaderen.
Prof Li zei:"Het dynamische systeemperspectief van deep learning biedt een veelbelovend wiskundig raamwerk dat de onderscheidende aspecten van diepe neurale netwerken benadrukt in vergelijking met traditionele paradigma's. Dit brengt spannende nieuwe wiskundige problemen met zich mee op het raakvlak van dynamische systemen, benaderingstheorie en machine learning. "
"Een veelbelovend gebied voor toekomstige ontwikkeling is om dit raamwerk uit te breiden om andere aspecten van diepe neurale netwerken te bestuderen, zoals hoe ze effectief te trainen en hoe ervoor te zorgen dat ze beter werken op ongeziene datasets", voegde prof. Li toe. + Verder verkennen
Rationeel neuraal netwerk bevordert het leren van partiële differentiatievergelijkingen
 Wetenschappers ontcijferen het multi-domein, volledige structuur van de humane smoothened receptor
Wetenschappers ontcijferen het multi-domein, volledige structuur van de humane smoothened receptor Berekening van Valency
Berekening van Valency Het overwinnen van de uitdagingen bij gecontroleerde thermische depositie van organische diradicalen
Het overwinnen van de uitdagingen bij gecontroleerde thermische depositie van organische diradicalen Hoe lineaire en ringvormige moleculen te scheiden?
Hoe lineaire en ringvormige moleculen te scheiden? Polymeerfilms slagen voor de elektronenkanontest
Polymeerfilms slagen voor de elektronenkanontest
Hoofdlijnen
- Oude levensvorm ontdekt in afgelegen Tasmaanse vallei
- Wetenschappers ontdekken nieuwe uitgestorven mierensoorten ingekapseld in barnsteen
- Franse regering verklaart de oorlog aan pesticiden
- Hoe klimaatverandering subalpiene wilde bloemengemeenschappen kan hervormen
- Tijdgebonden eten vermindert cardiovasculaire gezondheidsrisico's die samenhangen met ploegenarbeid voor brandweerlieden
- Microbioomtransplantaties bieden ziekteresistentie in ernstig bedreigde Hawaiiaanse plant
- Chili vecht om een favoriete mossel te redden
- Recordaantal walvissen geteld in Patagonië in Argentinië
- VS zegt dat sneeuwminnende lynx geen speciale bescherming meer nodig heeft
- Jane Goodall:een mondiaal gezicht voor wereldwijde vrede

- Tanden van Homo antecessor werpen licht op trends in de tandevolutie van de pleistocene mensachtigen
- Oude site op de Westelijke Jordaanoever trekt christenen, en controverse

- Archeologen bestuderen hoe loodvergiftiging het Romeinse rijk beïnvloedde

- Analyse van overblijfselen in een oud graf geeft inzicht in de neolithische geschiedenis in Polen

 Radicale breuken eenvoudiger maken
Radicale breuken eenvoudiger maken Voordelen en nadelen van Convex Mirrors
Voordelen en nadelen van Convex Mirrors  Maak een lijst van drie factoren die van invloed zijn op de windrichting
Maak een lijst van drie factoren die van invloed zijn op de windrichting Bereken het drumvolume
Bereken het drumvolume  Onderzoekers manipuleren collectieve dynamiek in magnetische nanostructuren
Onderzoekers manipuleren collectieve dynamiek in magnetische nanostructuren Microsoft staat kort bovenaan Apple als meest waardevolle bedrijf
Microsoft staat kort bovenaan Apple als meest waardevolle bedrijf Oude luizenachtige insecten gevonden om zich te voeden met dinosaurusveren
Oude luizenachtige insecten gevonden om zich te voeden met dinosaurusveren Taiheiyo Evergreen Forest Animals
Taiheiyo Evergreen Forest Animals
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

