
Wetenschap
Wiskundige ontdekt voorwaarden voor stabilisatie van differentiële ongelijkheden van hogere orde
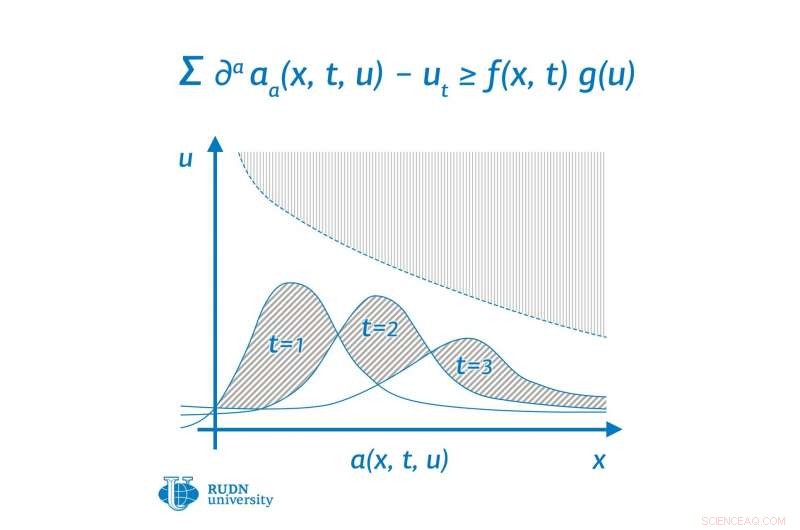
Krediet:RUDN University
Een wiskundige van de RUDN University (Rusland) en een collega hebben de voorwaarden voor stabilisatie van differentiële ongelijkheden van hoge orde bepaald. Met dit resultaat kunnen wiskundigen beperkingen opleggen aan de oplossingen van vergelijkingen die sommige fysische processen beschrijven, zoals diffusieprocessen en convectieprocessen. Het artikel is gepubliceerd in het tijdschrift Asymptotische analyse .
Interesse in differentiële ongelijkheden komt voort uit een groot aantal wiskundige modelleringsproblemen in de natuurwetenschappen, evenals bij het oplossen van technische en fysieke problemen. Het is vaak nodig om verschillende functies te definiëren die verband houden met verschillende differentiële ongelijkheden. Hiervoor is een gelijk aantal ongelijkheden nodig. Als elk van deze ongelijkheden differentieel is, dat is, heeft de vorm van een relatie die onbekende functies en hun afgeleiden verbindt, dit is een systeem van differentiële ongelijkheden. Systemen van differentiële ongelijkheden beschrijven echte fysieke processen met een zekere mate van nauwkeurigheid (bijvoorbeeld apparaten die fysieke verschijnselen registreren, zijn niet perfect en bevatten enkele fouten). Het kan blijken dat een kleine fout in de initiële gegevens significante veranderingen veroorzaakt in de oplossing van de ongelijkheid. Daarom, het is belangrijk om limieten te stellen aan de oplossingen van differentiaalvergelijkingen.
Andrey Shishkov van S.M. Nikol'skii Mathematisch Instituut van de RUDN Universiteit en Andrej Kon'kov van de Staatsuniversiteit van Moskou verkregen het resultaat, die de klassieke Keller-Osserman-voorwaarde voor differentiaalvergelijkingen generaliseert. De stelling van Keller-Osserman bevat voorwaarden voor het ontbreken van positieve oplossingen voor niet-lineaire elliptische ongelijkheden van de tweede orde. Deze stelling dient als basis voor studies naar de afwezigheid van oplossingen voor vergelijkingen en ongelijkheden. Bovendien, voor differentiële operatoren van hoge orde, alle eerder bekende onderzoeken waren beperkt tot het geval van niet-lineariteit van de macht. Het geval van willekeurige niet-lineariteit is alleen bestudeerd voor tweede-orde-operators. Wiskundigen hebben differentiële ongelijkheden van hogere ordes onderzocht en hun resultaat is van toepassing op een brede klasse van problemen - vergelijkingen van de tweede en derde orde.
De resultaten kunnen worden toegepast op zowel parabolische als zogenaamde anti-parabolische ongelijkheden. Parabolische vergelijkingen zijn wijdverbreid in de natuurkunde:deze omvatten vergelijkingen die de processen van convectie beschrijven, diffusie en het specifieke geval - de warmtegeleidingsvergelijking; het Navier-Stokes-systeem van vergelijkingen dat de beweging van vloeistoffen en gassen beschrijft, is een systeem van parabolische vergelijkingen met uiteenlopende beperkingen.
De vragen werden voorheen voornamelijk bestudeerd voor differentiaaloperatoren van de tweede orde, en het geval van hogere-orde operators is veel minder bestudeerd. Wiskundigen deden onderzoek naar differentiële ongelijkheden van hogere orde en verkregen voldoende stabilisatiecondities voor zogenaamde zwakke oplossingen van differentiële ongelijkheden. Tegelijkertijd, de beginvoorwaarden worden niet gesteld aan de oplossingen van de bestudeerde differentiaalongelijkheid. De auteurs stellen ook geen ellipticiteitsvoorwaarden voor de coëfficiënten van de differentiaaloperator.
 Polymeeronderzoekers ontdekken pad naar duurzame en biologisch afbreekbare polyesters
Polymeeronderzoekers ontdekken pad naar duurzame en biologisch afbreekbare polyesters Vooruitgang in de richting van het aansluiten van een antibioticapomp
Vooruitgang in de richting van het aansluiten van een antibioticapomp Onderzoekers presenteren een microbiële stam die in staat is tot massale barnsteenzuurproductie
Onderzoekers presenteren een microbiële stam die in staat is tot massale barnsteenzuurproductie Zoals de hond van Pavlov, deze thermoplast leert een nieuwe truc:lopen
Zoals de hond van Pavlov, deze thermoplast leert een nieuwe truc:lopen Uitvinding biedt nieuwe optie voor het bewaken van de gezondheid van het hart
Uitvinding biedt nieuwe optie voor het bewaken van de gezondheid van het hart
Hoofdlijnen
- Wat zijn emoties,
- Waarom door deuropeningen lopen ons doet vergeten
- DNA versus RNA: wat zijn de overeenkomsten en verschillen? (met diagram)
- Onderzoek toont aan dat walvissen, al een bedreigde diersoort, kan een vage toekomst tegemoet gaan
- Wat zijn de sporten op het DNA Dubbelschroef gemaakt van?
- Tropische vogel waarschijnlijk uit koers geblazen door orkaan Jose
- Research Paper Onderwerpen in Biochemistry
- Zal er ooit een gelukkige pil zijn?
- Het ochtendkoor horen:Okina was een nieuw akoestisch monitoringnetwerk
- Google-zoekgegevens onthullen Amerikaanse zorgen over abortus

- Stimulans voor het aanpassen van woningen kan ook de energierekening en ongelijkheid verminderen

- Oudste verwant van zagers en regenwormen

- Waarom is het Pentagon geïnteresseerd in UFO's?

- Enquête toont aan dat nieuwe levensstijlvoorkeuren een nieuw tijdperk voor de werkplek inluiden

 Klokkenluider Cambridge Analytica roept op tot online regulering
Klokkenluider Cambridge Analytica roept op tot online regulering Complexe dynamiek maakt meerwater groen en bruin
Complexe dynamiek maakt meerwater groen en bruin Onderzoekers documenteren een kwantumspingolf voor licht
Onderzoekers documenteren een kwantumspingolf voor licht Experts proberen te voorkomen dat schilderijen van Georgia OKeeffe vervagen
Experts proberen te voorkomen dat schilderijen van Georgia OKeeffe vervagen Schonere lucht met aardwarmte
Schonere lucht met aardwarmte Quantum dots nemen efficiënte beslissingen
Quantum dots nemen efficiënte beslissingen Hoogte, breedte en vierkante voet berekenen
Hoogte, breedte en vierkante voet berekenen Om voedselverspilling tegen te gaan, we moeten misschien meer betalen voor wat we eten?
Om voedselverspilling tegen te gaan, we moeten misschien meer betalen voor wat we eten?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

