Om te leren hoe codebrekers geheime berichten kraken, je moet weten hoe mensen codes maken. In de volgende sectie, we zullen meer te weten komen over enkele van de eerste pogingen om berichten te verbergen.

1. Polybius-vierkanten en Caesar-verschuivingen
2. Het Trimethius-tableau
3. Het Vigenère-cijfer
4. ADFGX-codering
5. Codeermachines
6. cryptanalyse
7. De code breken
8. Beroemde onopgeloste codes

Polybius-vierkanten en Caesar-verschuivingen

Hoewel historische bevindingen aantonen dat verschillende oude beschavingen elementen van cijfers en codes gebruikten in hun schrift, code-experts zeggen dat deze voorbeelden bedoeld waren om de boodschap een gevoel van belang en formaliteit te geven. De persoon die het bericht schrijft, is bedoeld om zijn publiek het te laten lezen.

De Grieken waren een van de eerste beschavingen die cijfers gebruikten om in het geheim te communiceren. Een Griekse geleerde genaamd Polybius stelde een systeem voor voor het vercijferen van een bericht waarin een cryptograaf elke letter voorstelde met een paar cijfers variërend van één tot vijf met behulp van een vierkant van 5 bij 5 (de letters I en J deelden een vierkant). Het Polybius-plein (ook wel het dambord genoemd) ziet er als volgt uit:

Een cryptograaf zou de letter "B" als "12" schrijven. De letter O is "34". Om de uitdrukking "Hoe dingen werken, " zou de cryptograaf "233452 4344452121 5234422543" schrijven. Omdat hij elke letter vervangt door twee cijfers, het is moeilijk voor iemand die niet bekend is met de code om te bepalen wat dit bericht betekent. De cryptograaf zou het nog moeilijker kunnen maken door de volgorde van de letters door elkaar te halen in plaats van ze alfabetisch uit te schrijven.

Julius Caesar vond nog een vroeg cijfer uit - een die heel eenvoudig was en toch zijn vijanden in verwarring bracht. Hij creëerde vercijferde berichten door de volgorde van het alfabet met een bepaald aantal letters te verschuiven. Bijvoorbeeld, als je het Engelse alfabet drie plaatsen naar beneden zou schuiven, de letter "D" zou de letter "A, " terwijl de letter "E" "B" zou betekenen, enzovoort. Je kunt deze code visualiseren door de twee alfabetten op elkaar te schrijven met de bijbehorende leesbare tekst en cijfer die als volgt overeenkomen:

Merk op dat het cijferalfabet rondloopt naar "A" nadat het "Z" heeft bereikt. Met behulp van dit cijfersysteem, je zou de uitdrukking "Hoe dingen werken" kunnen vercijferen als "KRZ VWXII ZRUNV."

Beide systemen, het Polybiusplein en de Caesarverschuiving, vormden de basis van veel toekomstige codeersystemen.

In de volgende sectie, we zullen een paar van deze meer geavanceerde coderingsmethoden bekijken.

De taal ontcijferen Tot vercijferen een bericht betekent het vervangen van de letters in de tekst door het vervangende alfabet. Het leesbare bericht heet de platte tekst . De cryptograaf zet de leesbare tekst om in een cijfer en stuurt het door. De ontvanger van het bericht gebruikt de juiste techniek, genaamd de toets , om de boodschap te ontcijferen, het veranderen van een cijfer terug in een leesbare tekst.

Het Trimethius-tableau

Na de val van het Romeinse Rijk, de westerse wereld ging wat we nu de donkere middeleeuwen noemen binnen. Gedurende deze periode, beurs daalde en cryptografie onderging hetzelfde lot. Pas in de Renaissance werd cryptografie weer populair. De Renaissance was niet alleen een periode van intense creativiteit en leren, maar ook van intriges, politiek, oorlogvoering en bedrog.

Cryptografen gingen op zoek naar nieuwe manieren om berichten te vercijferen. De Caesar Shift was te gemakkelijk te kraken -- met genoeg tijd en geduld, bijna iedereen kon de leesbare tekst achter de gecodeerde tekst ontdekken. Koningen en priesters huurden geleerden in om nieuwe manieren te bedenken om geheime boodschappen te verzenden.

Een van die geleerden was Johannes Trimethius, die voorstelde om het alfabet in een matrix te leggen, of tableau . De matrix was 26 rijen lang en 26 kolommen breed. De eerste rij bevatte het alfabet zoals het normaal wordt geschreven. De volgende rij gebruikte een Caesar Shift om het alfabet over één spatie te verplaatsen. Elke rij verschoof het alfabet een andere plek, zodat de laatste rij begon met "Z" en eindigde op "Y". U kunt het alfabet normaal lezen door over de eerste rij of door de eerste kolom te kijken. Het ziet er zo uit:

Zoals je kunt zien, elke rij is een Caesar Shift. Om een ​​brief te vercijferen, de cryptograaf kiest een rij en gebruikt de bovenste rij als leesbare tekstgids. Een cryptograaf die de 10e rij gebruikt, bijvoorbeeld, zou de leesbare letter "A" als "J" vercijferen.

Trimethius stopte daar niet -- hij stelde voor dat cryptografen berichten vercijferen door de eerste rij voor de eerste letter te gebruiken, de tweede rij voor de tweede letter, en zo verder op het tableau. Na 26 opeenvolgende brieven, de cryptograaf zou dan weer bij de eerste rij beginnen en weer verder werken totdat hij het hele bericht had vercijferd. Met behulp van deze methode, hij kon de uitdrukking "How Stuff Works" vercijferen als "HPY VXZLM EXBVE."

Het tableau van Trimethius is een goed voorbeeld van een polyalfabetisch cijfer . De meeste vroege cijfers waren: monoalfabetisch , wat betekent dat één cijferalfabet het leesbare alfabet verving. Een polyalfabetisch cijfer gebruikt meerdere alfabetten om de leesbare tekst te vervangen. Hoewel in elke rij dezelfde letters worden gebruikt, de letters van die rij hebben een andere betekenis. Een cryptograaf vercijfert een leesbare tekst "A" in rij drie als een "C, " maar een "A" in rij 23 is een "W." Het systeem van Trimethius gebruikt daarom 26 alfabetten -- één voor elke letter in het normale alfabet.

In de volgende sectie, we zullen leren hoe een geleerde genaamd Vigenère een complex polyalfabetisch cijfer heeft gemaakt.

Het Vigenère-cijfer

In de late jaren 1500, Blaise de Vigenère stelde een polyalfabetisch systeem voor dat bijzonder moeilijk te ontcijferen is. Zijn methode gebruikte een combinatie van het Trimethius tableau en a toets . De sleutel bepaalde welk van de alfabetten in de tabel de ontcijferaar moest gebruiken, maar maakte niet per se deel uit van de eigenlijke boodschap. Laten we nog eens naar het Trimethius-tableau kijken:

Laten we aannemen dat u een bericht versleutelt met het sleutelwoord 'CIPHER'. Je zou de eerste letter vercijferen met behulp van de "C"-rij als richtlijn, met behulp van de letter gevonden op de kruising van de "C"-rij en de kolom van de corresponderende leesbare letter. Voor de tweede brief je zou de "I" rij gebruiken, enzovoort. Zodra u de rij "R" gebruikt om een ​​letter te vercijferen, je zou terug beginnen bij "C". Met behulp van dit sleutelwoord en deze methode, je zou "How Stuff Works" op deze manier kunnen vercijferen:

Uw vercijferde bericht zou lezen, "JWL ZXLHN LVVBU." Als je een langer bericht wilt schrijven, je zou de sleutel keer op keer herhalen om je leesbare tekst te vercijferen. De ontvanger van uw bericht moet de sleutel van tevoren weten om de tekst te kunnen ontcijferen.

Vigenère suggereerde een nog complexer schema dat gebruik maakte van a priming brief gevolgd door het bericht zelf als de sleutel. De priming letter duidde de rij aan die de cryptograaf als eerste gebruikte om het bericht te beginnen. Zowel de cryptograaf als de ontvanger wisten vooraf welke priming letter ze moesten gebruiken. Deze methode maakte het kraken van cijfers extreem moeilijk, maar het kostte ook veel tijd en een fout in het begin van het bericht kan alles wat volgde verminken. Terwijl het systeem veilig was, de meeste mensen vonden het te complex om effectief te gebruiken. Hier is een voorbeeld van het systeem van Vigenère -- in dit geval is de beginletter " NS ":

te ontcijferen, de ontvanger zou eerst naar de eerste letter van het versleutelde bericht kijken, een "K" in dit geval, en gebruik de Trimethius-tabel om te vinden waar de "K" viel in de rij "D" -- onthoud, zowel de cryptograaf als de ontvanger weten vooraf dat de eerste letter van de sleutel altijd "D, " ongeacht wat de rest van het bericht zegt. De letter bovenaan die kolom is "H." De "H" wordt de volgende letter in de sleutel van het cijfer, dus de ontvanger zou vervolgens naar de rij "H" kijken en de volgende letter in het cijfer vinden - in dit geval een "V". Dat zou de ontvanger een "O" geven. Door deze methode te volgen, de ontvanger kan het hele bericht ontcijferen, al duurt het even.

Het complexere Vigenère-systeem sloeg pas aan in de jaren 1800, maar het wordt nog steeds gebruikt in moderne codeermachines [bron:Kahn].

In de volgende sectie, we zullen meer te weten komen over de ADFGX-code die door Duitsland is gemaakt tijdens de Eerste Wereldoorlog.

ADFGX-codering

Na de uitvinding van de telegraaf, het was nu mogelijk voor individuen om onmiddellijk over hele landen te communiceren met behulp van morsecode. Helaas, het was ook mogelijk voor iedereen met de juiste apparatuur om een ​​lijn af te tappen en mee te luisteren op centrales. Bovendien, de meeste mensen moesten vertrouwen op griffiers om berichten te coderen en te decoderen, waardoor het onmogelijk is om clandestien platte tekst te verzenden. Alweer, cijfers werden belangrijk.

Duitsland creëerde een nieuw cijfer op basis van een combinatie van het Polybius-dambord en cijfers met sleutelwoorden. Het stond bekend als het ADFGX-cijfer, omdat dat de enige letters waren die in het cijfer werden gebruikt. De Duitsers kozen deze letters omdat hun morsecode-equivalenten moeilijk te verwarren zijn, het verkleinen van de kans op fouten.

De eerste stap was om een ​​matrix te maken die veel op het Polybius-dambord leek:

Cryptografen zouden paren cijferletters gebruiken om leesbare letters weer te geven. De rij van de letter wordt het eerste cijfer in het paar, en de kolom wordt het tweede cijfer. In dit voorbeeld, de vercijferde letter "B" wordt "AD, " terwijl "O" "FG" wordt. Niet alle ADFGX-matrices hadden het alfabet in alfabetische volgorde uitgezet.

Volgende, de cryptograaf zou zijn bericht vercijferen. Laten we het bij 'Hoe dingen werken' houden. Met behulp van deze matrix, we zouden "DFFGXD GFGGGXDADA XDFGGDDXGF" krijgen.

De volgende stap was het bepalen van een sleutelwoord, die elke lengte kan hebben, maar geen herhaalde letters kan bevatten. Voor dit voorbeeld, we zullen het woord gebruiken DEUTSCH . De cryptograaf zou een raster maken met het sleutelwoord bovenaan gespeld. De cryptograaf zou dan het vercijferde bericht in het raster schrijven, de cijferparen in afzonderlijke letters splitsen en van de ene rij naar de andere wikkelen.

Volgende, de cryptograaf zou het raster herschikken zodat de letters van het sleutelwoord in alfabetische volgorde stonden, de corresponderende kolommen van de letters dienovereenkomstig verschuiven:

Hij zou dan het bericht uitschrijven door elke kolom naar beneden te volgen (zonder rekening te houden met de letters van het sleutelwoord op de bovenste rij). Dit bericht zou verschijnen als "DDG DFDD FGAD GAG XXFF GGDG FGXX." Het is waarschijnlijk duidelijk waarom deze code zo uitdagend was -- cryptografen vercijferden en getransponeerd elk leesteken. Om te decoderen, je zou het sleutelwoord (DEUTSCH) moeten kennen, dan zou je vanaf daar achteruit werken. Je zou beginnen met een raster met de kolommen alfabetisch gerangschikt. Als je het eenmaal hebt ingevuld, je zou de kolommen correct kunnen herschikken en je matrix gebruiken om het bericht te ontcijferen.

Woorden tellen Een van de manieren waarop u een sleutelwoord in een ADFGX-cijfer kunt raden, is door het aantal woorden in het gecodeerde bericht te tellen. Het aantal gecodeerde woorden geeft aan hoe lang het sleutelwoord is -- elk gecodeerd woord vertegenwoordigt een tekstkolom, en elke kolom komt overeen met een letter in het sleutelwoord. In ons voorbeeld, er zijn zeven woorden in de gecodeerde boodschap, wat betekent dat er zeven kolommen zijn met een sleutelwoord van zeven letters. Zowaar, DEUTSCH heeft zeven letters. Omdat de gecodeerde woorden en het originele bericht verschillende woordentellingen kunnen hebben - zeven gecodeerde woorden versus drie platte tekstwoorden in ons voorbeeld - wordt het ontcijferen van het bericht een grotere uitdaging.

In de volgende sectie, we zullen kijken naar enkele van de apparaten die cryptografen hebben uitgevonden om raadselachtige cijfers te maken.

Codeermachines

Een van de vroegst bekende versleutelingsapparaten is de Alberti-schijf, uitgevonden door Leon Battista Alberti, in de 15e eeuw. Het apparaat bestond uit twee schijven, de binnenste bevat een gecodeerd alfabet en de buitenste een tweede, afgekapt alfabet en de cijfers 1 tot 4. De buitenste schijf roteerde om verschillende letters te matchen met de binnenste cirkel, welke letters de cryptograaf als leesbare tekst gebruikte. De letters van de buitenste schijf dienden toen als cijfertekst.

William West/AFP/Getty Images
Dan Brown's roman "The Da Vinci Code" volgt de avonturen
van een professor symboliek terwijl hij codes en cijfers oplost, sommige
waarvan hij breekt met behulp van een Cardano Grille.

Omdat het alfabet van de binnenste schijf vervormd was, de ontvanger zou een identieke kopie nodig hebben van de schijf die de cryptograaf heeft gebruikt om het bericht te ontcijferen. Om het systeem veiliger te maken, de cryptograaf kan de uitlijning van de schijf veranderen in het midden van een bericht, misschien na drie of vier woorden. De cryptograaf en ontvanger zouden weten dat ze de schijfinstellingen moeten wijzigen na een voorgeschreven aantal woorden, misschien eerst de schijf zo instellen dat de binnenste cirkel "A" overeenkomt met de buitenste cirkel "W" voor de eerste vier woorden, dan met "N" voor de volgende vier, enzovoort. Dit maakte het kraken van het cijfer veel moeilijker.

Cardano-roosters en steganografie Een slimme manier om een ​​geheime boodschap te verbergen is duidelijk zichtbaar. Een manier om dit te doen is door a Cardano-rooster -- een stuk papier of karton met uitgesneden gaten. Om een ​​bericht te coderen, je legt een rooster op een blanco vel papier en schrijft je boodschap door de gaten van het rooster. Je vult de rest van het papier met onschuldige tekst. Wanneer uw ontvanger het bericht ontvangt, hij legt er een identiek rooster over om de geheime tekst te zien. Dit is een vorm van steganografie , het verbergen van een bericht in iets anders.

In de 19de eeuw, Thomas Jefferson stelde een nieuwe codeermachine voor. Het was een cilinder van schijven gemonteerd op een spindel. Op de rand van elke schijf stonden de letters van het alfabet, in willekeurige volgorde gerangschikt. Een cryptograaf zou de schijven kunnen uitlijnen om een ​​kort bericht over de cilinder te spellen. Hij zou dan naar een andere rij over de cilinder kijken, dat lijkt op gebrabbel, en stuur dat naar de ontvanger. De ontvanger zou een identieke cilinder gebruiken om de reeks onzinbrieven te spellen, scan dan de rest van de cilinder, op zoek naar een bericht in het Engels. 1922, het Amerikaanse leger nam een ​​apparaat aan dat erg op dat van Jefferson leek; andere takken van het leger volgden al snel het voorbeeld [bron:Kahn].

Misschien wel het meest bekende versleutelingsapparaat was dat van Duitsland Enigma-machine uit het begin van de 20e eeuw. De Enigma Machine leek op een typemachine, maar in plaats van lettertoetsen had het een reeks lampjes met op elk een letter gestempeld. Door op een toets te drukken, liep er een elektrische stroom door een complex systeem van draden en tandwielen, resulterend in een vercijferde letter verhelderend. Bijvoorbeeld, u kunt op de toets voor de letter "A" drukken en de "T" zien oplichten.

Foto met dank aan het Amerikaanse leger
Duitse soldaten met behulp van een
Enigma Machine in het veld.

Wat de Enigma Machine zo'n formidabel coderingsapparaat maakte, was dat zodra je op een letter drukte, een rotor in de machine zou draaien, het veranderen van de elektrodecontactpunten in de machine. Dit betekent dat als u een tweede keer op "A" drukt, een andere letter zou oplichten in plaats van "T." Elke keer dat u een letter typt, de rotor draaide, en na een bepaald aantal letters, een tweede rotor ingeschakeld, dan een derde. Met de machine kon de operator veranderen hoe brieven in de machine werden ingevoerd, zodat wanneer u op één letter drukt, de machine zou het interpreteren alsof u een andere letter had ingedrukt.

Hoe kraakt een cryptanalist zo'n moeilijke code? In de volgende sectie, we zullen leren hoe codes en cijfers worden gebroken.

cryptanalyse

Hoewel er honderden verschillende codes en coderingssystemen in de wereld zijn, er zijn enkele universele eigenschappen en technieken die cryptanalisten gebruiken om ze op te lossen. Geduld en doorzettingsvermogen zijn twee van de belangrijkste eigenschappen van een cryptanalist. Het oplossen van een cijfer kan veel tijd kosten, soms moet u op uw stappen terugkeren of opnieuw beginnen. Het is verleidelijk om op te geven als je wordt geconfronteerd met een bijzonder uitdagende code.

Een andere belangrijke vaardigheid om te hebben is een sterke bekendheid met de taal waarin de leesbare tekst is geschreven. Het is bijna onmogelijk om een ​​gecodeerd bericht in een onbekende taal op te lossen.

Navajo Code Talkers Tijdens de Tweede Wereldoorlog, de Verenigde Staten gebruikten Navajo Native Americans om berichten te coderen. De Navajo's gebruikten een codesysteem op basis van hoe hun taal in het Engels werd vertaald. Ze kenden termen als 'vliegtuig' toe aan codewoorden als 'Da-he-tih-hi, " wat "kolibrie" betekent. Om woorden te vercijferen die geen corresponderend codewoord hadden, ze gebruikten een gecodeerd alfabet. Dit gecodeerde alfabet gebruikte Navajo-vertalingen van Engelse woorden om letters weer te geven; bijvoorbeeld, het Navajo-woord "wol-la-chee" betekende "mier, " zodat "wol-la-chee" voor de letter "a" zou kunnen staan. Sommige letters werden vertegenwoordigd door meerdere Navajo-woorden. De Navajo-taal was zo vreemd voor de Japanners, ze hebben de code nooit gebroken [bron:Kahn].

Een sterke bekendheid met een taal omvat ook een begrip van de taal ontslag .

Redundantie houdt in dat elke taal meer karakters of woorden bevat dan nodig zijn om informatie over te brengen. De regels van de Engelse taal creëren redundantie -- bijvoorbeeld, geen enkel Engels woord begint met de letters "ng." Engels is ook sterk afhankelijk van een klein aantal woorden. Woorden als "de, " "van, " "en, " "tot, " "een, " "in, " "Dat, " "het, " "is, " en "ik" zijn goed voor meer dan een kwart van de tekst van een gemiddeld bericht dat in het Engels is geschreven [bron:Kahn].

Het kennen van de overtollige kwaliteiten van een taal maakt de taak van een cryptanalist veel gemakkelijker. Hoe ingewikkeld het cijfer ook is, het volgt de regels van een bepaalde taal zodat de ontvanger het bericht kan begrijpen. Cryptanalisten zoeken naar patronen in cijfers om veelvoorkomende woorden en lettercombinaties te vinden.

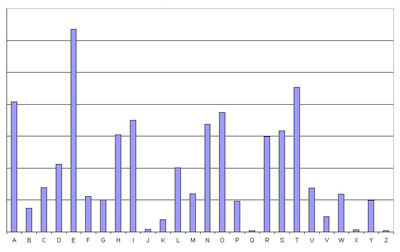
Een basistechniek in cryptanalyse is: frequentie analyse . Elke taal gebruikt bepaalde letters vaker dan andere. In Engels, de letter "e" is de meest voorkomende letter. Door de karakters in een tekst op te tellen, een cryptanalist kan heel snel zien wat voor soort cijfer hij heeft. Als de verdeling van de cijferfrequentie vergelijkbaar is met de verdeling van de frequentie van een normaal alfabet, de cryptanalist kan concluderen dat hij te maken heeft met een monoalfabetisch cijfer.

©HowStuffWorks 2007
Deze grafiek toont de frequentie waarmee
elke letter in de Engelse taal wordt gebruikt.

In de volgende sectie, we zullen kijken naar meer complexe cryptanalyse en de rol die geluk speelt bij het breken van een cijfer.

Kneepjes van het vak Cryptografen gebruiken veel methoden om cryptoanalisten te verwarren. acrofonie is een methode die een letter codeert door een woord te gebruiken dat begint met de klank van die letter. "Bat" kan staan ​​voor "b, " terwijl "sluwheid" zou kunnen staan ​​voor "k." A polyfoon is een symbool dat meer dan één letter van leesbare tekst vertegenwoordigt -- een "%" kan bijvoorbeeld zowel een "r" als een "j" vertegenwoordigen, terwijl homofone substitutie gebruikt verschillende cijfers om dezelfde leesbare letter weer te geven -- "%" en "&" kunnen beide de letter "c" vertegenwoordigen. Sommige cryptografen gooien er zelfs in null-symbolen dat stelt helemaal niets voor.

De code breken

Meer gecompliceerde cijfers vereisen een combinatie van ervaring, experimenteren en af ​​en toe een gok in het donker. De moeilijkste cijfers zijn kort, doorlopende blokken tekens. Als het bericht van de cryptograaf bevat: woord pauzes , spaties tussen elk vercijferd woord, het maakt het ontcijferen veel gemakkelijker. De cryptanalist zoekt naar groepen herhaalde cijfers, analyseren waar die groepen letters binnen de context van woorden vallen en raden wat die letters zouden kunnen betekenen. Als de cryptanalist een idee heeft over de inhoud van het bericht, hij zou naar bepaalde woorden kunnen zoeken. Een cryptanalist die een bericht van een marinekapitein onderschept, kan zoeken naar termen die verwijzen naar weerpatronen of zeecondities. Als hij vermoedt dat 'hyuwna' 'stormachtig' betekent, 'Misschien kan hij de rest van het cijfer kraken.

Christopher Furlong/Getty Images
Het breken van de code die in het plafond van de Rosslyn-kapel in Schotland is uitgehouwen, onthult een reeks muzikale passages.

Veel polyalfabetische cijfers zijn gebaseerd op sleutelwoorden, wat de boodschap kwetsbaar maakt. Als de cryptoanalist het juiste sleutelwoord raadt, hij kan het hele bericht snel ontcijferen. Het is belangrijk voor cryptografen om sleutelwoorden regelmatig te veranderen en ongebruikelijke of onzinnige sleutelwoorden te gebruiken. Het onthouden van een onzinsleutelwoord kan een uitdaging zijn, en als u uw coderingssysteem zo moeilijk maakt dat uw ontvanger het bericht niet snel kan ontcijferen, uw communicatiesysteem faalt.

Cryptanalisten maken gebruik van elke mogelijkheid om een ​​cijfer op te lossen. Als de cryptograaf een coderingsapparaat heeft gebruikt, een slimme cryptanalist zal proberen hetzelfde apparaat te krijgen of er een te maken op basis van zijn theorieën over de methodologie van de cryptograaf. Tijdens de Tweede Wereldoorlog, Poolse cryptanalisten bemachtigden een Enigma Machine en waren dicht bij het uitvogelen van het Duitse coderingssysteem toen het te gevaarlijk werd om door te gaan. De Polen wisselden hun informatie en technologie uit met de geallieerden, die hun eigen Enigma-machines maakten en veel van de gecodeerde berichten van Duitsland ontcijferden.

Moderne versleutelingsmethoden op hoog niveau zijn gebaseerd op wiskundige processen die relatief eenvoudig te maken zijn, maar uiterst moeilijk te ontcijferen. Encryptie met openbare sleutel is een goed voorbeeld. Het gebruikt twee sleutels:een voor het coderen van een bericht en een voor het decoderen. De coderingssleutel is de openbare sleutel, beschikbaar voor iedereen die met de houder van de geheime sleutel wil communiceren. De geheime sleutel decodeert berichten die zijn versleuteld met de openbare sleutel en vice versa. Voor meer informatie over versleuteling met openbare sleutels, zie Hoe versleuteling werkt.

De complexe algoritmen die cryptografen gebruiken, zorgen voorlopig voor geheimhouding. Dat zal veranderen als quantum computing een realiteit wordt. Kwantumcomputers konden de factoren van een groot aantal veel sneller vinden dan een klassieke computer. Als ingenieurs een betrouwbare kwantumcomputer bouwen, vrijwel elk versleuteld bericht op internet zal kwetsbaar zijn. Voor meer informatie over hoe cryptografen van plan zijn om met problemen om te gaan, lees Hoe Quantum Encryptie werkt.

In de volgende sectie, we kijken naar enkele codes en cijfers die onopgelost blijven, tot grote ergernis van cryptoanalisten.

Beroemde onopgeloste codes

Hoewel de meeste cryptoanalisten je dat zullen vertellen, theoretisch, er bestaat niet zoiets als een onbreekbare code, een paar cryptografen hebben codes en cijfers gemaakt die niemand heeft weten te kraken. In de meeste gevallen, er is gewoon niet genoeg tekst in het bericht voor cryptanalisten om te analyseren. Soms, het systeem van de cryptograaf is te complex, of er kan helemaal geen bericht zijn - de codes en cijfers kunnen bedrog zijn.

In de jaren 1800, een pamflet met drie versleutelde berichten begon te verschijnen in een kleine gemeenschap in Virginia. Het pamflet beschreef de avonturen van een man, Beale genaamd, die rijk was geworden door op zoek te gaan naar goud. naar verluidt, Beale had het grootste deel van zijn rijkdom op een geheime locatie verborgen en liet een gecodeerde boodschap achter die leidde naar de locatie van de schat bij een herbergier. Twintig jaar gingen voorbij zonder bericht van Beale, en de herbergier zocht hulp bij het oplossen van de gecodeerde berichten. Eventueel, iemand heeft vastgesteld dat een van de berichten de onafhankelijkheidsverklaring als codeboek gebruikte, maar het ontcijferde bericht gaf slechts vage hints over de locatie van de schat en beweerde dat de andere berichten er rechtstreeks naar toe zouden leiden. Niemand heeft een van de andere berichten opgelost, en velen geloven dat de hele zaak een hoax is.

De Zodiac-moordenaar stuurde gecodeerde berichten zoals deze naar
San Francisco kranten
In de jaren 1960.

Halverwege de jaren zestig, inwoners van San Francisco en omliggende provincies waren doodsbang voor een wrede moordenaar die de politie beschimpte met gecodeerde berichten. De moordenaar noemde zichzelf de Zodiac en stuurde de meeste van zijn brieven naar San Francisco kranten, af en toe een lang gecodeerd bericht over drie kranten verdelen. Naar men zegt, de cijfers verbijsterden wetshandhavings- en inlichtingendiensten, hoewel amateur-cryptanalisten erin slaagden de meeste van hen te kraken. Er zijn een paar berichten die nooit zijn opgelost, sommigen zouden een aanwijzing kunnen zijn voor de identiteit van de moordenaar.

Richard Feynman, natuurkundige en pionier op het gebied van nanotechnologie, ontving drie gecodeerde berichten van een wetenschapper in Los Alamos en deelde ze met zijn afgestudeerde studenten toen hij ze zelf niet kon ontcijferen. Momenteel, ze staan ​​op een puzzelsite. Cryptanalisten zijn er alleen in geslaagd om het eerste bericht te ontcijferen, wat de openingsregels bleken te zijn van Chaucer's "Canterbury Tales", geschreven in het Midden-Engels.

In 1990, Jim Sanborn creëerde een sculptuur genaamd Kryptos voor het CIA-hoofdkwartier in Langley, Va. Kryptos bevat vier vercijferde berichten, maar cryptanalisten hebben er slechts drie opgelost. Het laatste bericht heeft zeer weinig tekens (ofwel 97 of 98, afhankelijk van of een teken echt bij het vierde bericht hoort), waardoor het erg moeilijk te analyseren is. Verschillende mensen en organisaties hebben opgeschept over het oplossen van de andere drie berichten, inclusief de CIA en de NSA.

Hoewel deze berichten samen met vele andere vandaag de dag onopgelost zijn, er is geen reden om aan te nemen dat ze voor altijd onopgelost zullen blijven. Al meer dan 100 jaar, een gecodeerd bericht geschreven door Edgar Allen Poe onopgelost bleef, raadselachtige professionele en amateur-cryptanalisten. Maar in 2000, een man genaamd Gil Broza kraakte het cijfer. Hij ontdekte dat het cijfer meerdere homofone vervangingen gebruikte -- Poe had 14 cijfers gebruikt om de letter "e" weer te geven -- evenals verschillende fouten. Broza's werk bewijst dat het feit dat een code niet is opgelost, niet betekent dat deze niet oplosbaar is [bron:Elonka.com].