
Wetenschap
Een auto van 1250 kg die met een snelheid van 32,0 m/s door de straat rijdt, botst tegen een auto die ervoor geparkeerd staat en een massa van 875 kg heeft. beweegt 6 m/s weg?
Het initiële momentum van het systeem is:
$$P_i =m_1v_1 + m_2v_2$$
waar:
$$m_1$$ is de massa van de eerste auto (1250 kg)
$$v_1$$ is de snelheid van de eerste auto (32,0 m/s)
$$m_2$$ is de massa van de tweede auto (875 kg)
$$v_2$$ is de snelheid van de tweede auto (0 m/s, aangezien deze aanvankelijk geparkeerd staat)
Het uiteindelijke momentum van het systeem is:
$$P_f =(m_1 + m_2)v_f$$
waar:
$$v_f$$ is de eindsnelheid van de twee auto's, die we willen vinden
Als we het initiële momentum gelijk stellen aan het uiteindelijke momentum, krijgen we:
$$m_1v_1 + m_2v_2 =(m_1 + m_2)v_f$$
Als we $$v_f$$ oplossen, krijgen we:
$$v_f =\frac{m_1v_1 + m_2v_2}{m_1 + m_2}$$
Als we de gegeven waarden vervangen, krijgen we:
$$v_f =\frac{(1250 \text{ kg})(32,0 \text{ m/s}) + (875 \text{ kg})(0 \text{ m/s})}{1250 \text{ kg} + 875 \text{ kg}}$$
$$v_f =\frac{40000 \text{ kg m/s}}{2125 \text{ kg}}$$
$$v_f =18,8 m/s$$
Daarom rijden de twee auto's weg met een snelheid van 18,8 m/s.
 Door licht geactiveerde metaalkatalysator vernietigt vitale energiebron van kankercellen
Door licht geactiveerde metaalkatalysator vernietigt vitale energiebron van kankercellen Welk materiaal wordt gebruikt bij het maken van thermistors?
Welk materiaal wordt gebruikt bij het maken van thermistors?  Wetenschappers werken aan het maken van microchip-elementen van moleculaire grootte
Wetenschappers werken aan het maken van microchip-elementen van moleculaire grootte Element 3 lithium heeft één valentie-elektron en element 4 beryllium twee elektronen 5 boor hoeveel elektronen?
Element 3 lithium heeft één valentie-elektron en element 4 beryllium twee elektronen 5 boor hoeveel elektronen?  Wat wordt er gebruikt in een atoombom?
Wat wordt er gebruikt in een atoombom?
 Onderzoeksteam ontdekt dat soorten perceptuele vermogens delen die van invloed zijn op de manier waarop communicatie evolueert
Onderzoeksteam ontdekt dat soorten perceptuele vermogens delen die van invloed zijn op de manier waarop communicatie evolueert  NASA vindt Tropical Storm 07W nabij Kadena Air Base, Okinawa
NASA vindt Tropical Storm 07W nabij Kadena Air Base, Okinawa Hoe kan een land zich vermenigvuldigen?
Hoe kan een land zich vermenigvuldigen?  Welke dieren eten teken van herten?
Welke dieren eten teken van herten?  Superdiepe diamanten bevatten mogelijk nieuwe informatie over het binnenste van de aarde
Superdiepe diamanten bevatten mogelijk nieuwe informatie over het binnenste van de aarde
Hoofdlijnen
- Australische hagedissen eisen tol van schildpadeieren
- Kunnen we de taal van onze neven en nichten van primaten decoderen?
- Orka's migreren, studievondsten, maar waarom?
- Tsjaad breidt belangrijk natuurgebied in nationaal park uit
- Nutrient Agar vs. Blood Agar
- Wat is Ribonucleic Acid?
- De Dolly-erfenis:eet jij gekloond vlees?
- Hoe chimere, druppelvormende eiwitten kunnen bijdragen aan kanker
- Hoe kan een mutatie in DNA de eiwitsynthese beïnvloeden?
- Methode gevonden om fotonen elkaar af te stoten in een ultrakoud atomair gas
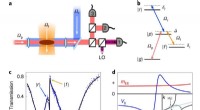
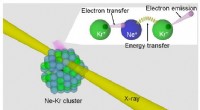
- Hoe röntgenstraling in materie genetische toxische laagenergetische elektronen creëert
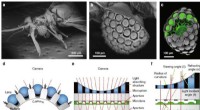
- Ultradunne digitale camera geïnspireerd op Xenos peckii-ogen
- Lokale symmetrie doorbreken - waarom water bevriest maar silica een glas vormt?

- Capillaire stroom wordt voor het eerst benut

 Wat is ondoorzichtig gas?
Wat is ondoorzichtig gas?  Wetenschapsbeurs over hoe vitamine C en ibuprofen de plantengroei beïnvloeden
Wetenschapsbeurs over hoe vitamine C en ibuprofen de plantengroei beïnvloeden Oude uitwerpselen onthullen hoe 'moerasdieet' de Vennen uit de Bronstijd met parasieten besmette
Oude uitwerpselen onthullen hoe 'moerasdieet' de Vennen uit de Bronstijd met parasieten besmette  Water + lucht + elektriciteit =waterstofperoxide
Water + lucht + elektriciteit =waterstofperoxide OSIRIS-REx-studenten vangen onverwachte glimp van zwart gat op
OSIRIS-REx-studenten vangen onverwachte glimp van zwart gat op Massatoerisme ontketent strijd om Montmartres ziel
Massatoerisme ontketent strijd om Montmartres ziel Hoe slimme bommen werken
Hoe slimme bommen werken  Hoe functies in Math
Hoe functies in Math
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

