
Wetenschap
Proton en een alfadeeltje komen vrij uit rust wanneer ze 0,225 van elkaar verwijderd zijn. Het heeft vier keer de massa en twee ladingen van een proton. Wat is maximale snelheid proton?
De initiële elektrische potentiële energie van het systeem is:
$$U_i=k\frac{(2q)(q)}{r_i}$$
Waar k de elektrostatische constante is en \(r_i=0,225m\). De uiteindelijke kinetische energie van het systeem is:
$$K_f=\frac{1}{2}mv_p^2+\frac{1}{2}(4m)v_\alpha^2$$
Waar \(v_p\) en \(v_\alpha\) respectievelijk de eindsnelheden van het proton- en alfadeeltje zijn.
Door het behoud van energie hebben we:
$$U_i=K_f$$
$$k\frac{(2q)(q)}{r_i}=\frac{1}{2}mv_p^2+2(4m)v_\alpha^2$$
$$k\frac{(2q)(q)}{0,225m}=\frac{1}{2}mv_p^2+8mv_\alpha^2$$
$$9\times10^9\frac{Nm^2}{C^2}\frac{2(1,6\times10^{-19}C)(1,6\times10^{-19}C)}{0,225m}=\frac{1}{2}(1,67\times10^{-19}kg)v_p^2+8(1,67\times10^{-27}kg)v_\alpha^2$$
$$7,94\times10^{-18}J=1,67\times10^{-27}kg(v_p^2+8v_\alpha^2)$$
$$4,74\times10^{9}m^2s^{-2}=v_p^2+8v_\alpha^2$$
Vanwege momentumbehoud hebben we:
$$0=(2q)v_p+(4q)v_\alpha$$
$$-2v_p=4v_\alpha$$
Vervanging in de vorige vergelijking:
$$4,74\times10^{9}m^2s^{-2}=v_p^2+8\left(-\frac{1}{2}v_p\right)^2$$
$$4,74\times10^{9}=v_p^2+v_p^2$$
$$4,74\times10^{9}=2v_p^2$$
$$v_p=\sqrt{\frac{4,74\times10^9}{2}}=\sqrt{2,37\times10^9}$$
$$\boxed{v_p=4,86\times10^4 m/s}$$
 Tropische regenwoudplanten voor kinderen
Tropische regenwoudplanten voor kinderen Uit onderzoek blijkt dat prehistorische pokdalige plekken op de zeebodem voor de kust van Californië in stand worden gehouden door krachtige sedimentstromen
Uit onderzoek blijkt dat prehistorische pokdalige plekken op de zeebodem voor de kust van Californië in stand worden gehouden door krachtige sedimentstromen  Wat de invasie van Oekraïne betekent voor het laatste klimaatveranderingsrapport van het IPCC
Wat de invasie van Oekraïne betekent voor het laatste klimaatveranderingsrapport van het IPCC Welke planeet heeft zure regenval?
Welke planeet heeft zure regenval?  Schotland zegt nee tegen fracken
Schotland zegt nee tegen fracken
Hoofdlijnen
- Genetische klokken bij zoöplanktonsoorten reguleren wat waarschijnlijk de grootste dagelijkse beweging van biomassa ter wereld is
- Hands-on Science-activiteiten over bloed
- Uit onderzoek blijkt dat de conservatieve en liberale eigenschappen van mensen terug te vinden zijn in hun Twitter-vocabulaire
- Onderzoekers identificeren hoe bacterie overleeft in zuurstofarme omgevingen
- Wat zijn de complementaire basen voor de volgende DNA-streng aatggccttagcagttgcatga?
- Droogte decimeert de belangrijkste katoenoogst in Texas
- Verbeteringen in de cryo-elektronenmicroscopie brengen het leven op atomair niveau duidelijker in beeld
- Soorten zenuwen in het menselijk lichaam
- Nieuwe coronavirussen zijn het meest riskant voor overloop
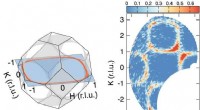
- Neutronen bewijzen het bestaan van spiraalvormige spinvloeistof
- Terwijl Run 3 begint, prijst CERN de ontdekking van exotische deeltjes

- Proton-kern-smashups leveren aanwijzingen op over quark-gluon-plasma

- Verborgen kwantuminformatie extraheren uit een lichtbron

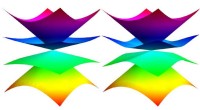
- Gluren in een wereld van spin-3/2 materialen
 Azijn bevat azijnzuur. De formule is:ch3cooh, één mol heeft een massa van?
Azijn bevat azijnzuur. De formule is:ch3cooh, één mol heeft een massa van?  Beantwoordt God gebeden? ASU-onderzoek zegt 'ja'
Beantwoordt God gebeden? ASU-onderzoek zegt 'ja'  Studie laat zien hoe weinig we weten over vrouwelijke terroristen
Studie laat zien hoe weinig we weten over vrouwelijke terroristen De verloren kunst van echt Damascus-staal
De verloren kunst van echt Damascus-staal  Ja, het heeft veel geregend, maar dat betekent niet dat de droogte in Australië is doorgebroken
Ja, het heeft veel geregend, maar dat betekent niet dat de droogte in Australië is doorgebroken Wat we weten over orkaan Irma:feiten, cijfers, voorspelling
Wat we weten over orkaan Irma:feiten, cijfers, voorspelling  Nucleaire technieken ontsluiten de structuur van een zeldzaam type supergeleidende intermetallische legering
Nucleaire technieken ontsluiten de structuur van een zeldzaam type supergeleidende intermetallische legering Nieuwe inzichten in de oorsprong van het leven
Nieuwe inzichten in de oorsprong van het leven
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

