Lassers en timmerlieden gebruiken allerlei gereedschappen om dingen in perfecte hoeken van 90 graden te zetten. Een snelle blik op de woordenlijst van een meetkundeboek zal je vertellen dat dit "rechte" hoeken worden genoemd.

We zien ze overal. Veel deurkozijnen hebben hoeken die in een rechte hoek zijn geplaatst. Dat geldt ook voor veel ramen, tapijten en koelkastmagneten. Om "The Red Green Show" te parafraseren, zijn ze het geheime wapen van een klusjesman.

Rechte hoeken moeten ook bekend zijn bij degenen onder ons die regelmatig naar teamsporten kijken. De volgende keer dat je favoriete NFL-ontvanger een touchdown scoort, let dan op de geverfde grasmat. De vier hoeken van de eindzone van een Amerikaans voetbalveld zijn allemaal hoeken van 90 graden. En dit zijn toevallig de bijproducten van loodrechte lijnen .

Loodrechte lijnen kruisen elkaar - of "snijden" elkaar in een rechte hoek. De oriëntatie onderscheidt ze van (onder andere) parallelle lijnen, die elkaar per definitie nooit, maar dan ook nooit snijden.

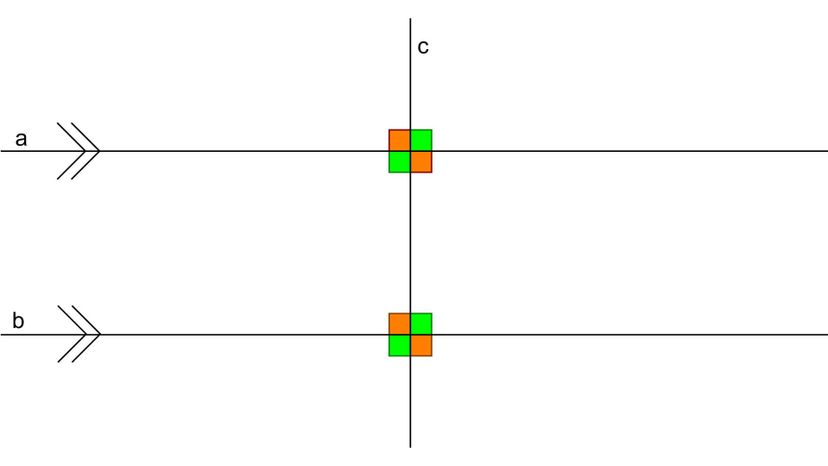
Maar er is nog een ander criterium. Als je technisch wilt worden, kruisen loodrechte lijnen elkaar niet alleen in hoeken van 90 graden; ze moeten ook coplanair . zijn . Het voorvoegsel "co-" geeft ons een hint over de betekenis van dit woord. Net als collega's die hun dagelijks brood verdienen in hetzelfde bedrijf, coplanair lijnen bestaan ​​op hetzelfde vlak.

Nee, dat betekent niet dat ze dezelfde vlucht hebben geboekt. We hebben het hier niet over vliegtuigen. Een geometrisch vlak is een plat, tweedimensionaal oppervlak. Hoewel ze niet dik zijn, strekken ze zich oneindig ver uit in zowel lengte als breedte.

Hoe dan ook, als je twee elkaar kruisende, coplanaire lijnen ziet en niet weet of ze loodrecht op elkaar staan, bestudeer dan hun hellingen . Kortom, de "helling" van een lijn is de maatstaf voor de steilheid.

Hellingen kunnen positief zijn of negatief . In grafieken stijgen lijnen met positieve hellingen steeds hoger boven de x-as, gezien van links naar rechts. Negatieve hellingen "bewegen" de andere kant op.

Ten slotte wordt gezegd dat een rechte lijn die evenwijdig aan de x-as loopt een helling nul heeft. Als een van deze "nul-slopers" (geen echte wiskundige term, maar wees gerust) een verticale lijn kruist die evenwijdig is aan de y-as, dan presto! Je hebt een paar loodrechte lijnen op je handen.

Dingen lopen niet altijd zo. Laten we aannemen dat uw snijdende lijnen niet parallel lopen met de x- en y-assen van de grafiek. Ze kunnen nog steeds loodrecht op elkaar staan, maar alleen als hun hellingen negatief omgekeerd zijn.

Om een ​​lang verhaal kort te maken, om de helling van een lijn te berekenen, moet je de stijging delen door zijn run . Een stijging is de verticale afstand tussen twee punten op een rechte lijn, gemeten in de eenheden op je grafiek. De runs lijken erg op elkaar, maar ze meten horizontale veranderingen.

Deel de stijging door de run en je krijgt een fractie. En "negatieve reciprocals" zijn in wezen omgedraaide breuken. De beste manier om dit uit te leggen is aan de hand van een voorbeeld:

Stel dat een van onze lijnen — die we "Lijn A" zullen noemen — een helling heeft die er als volgt uitziet:4/3

Als onze andere lijn — "Lijn B" — staat echt loodrecht op lijn A, dan verwachten we dat deze de volgende helling heeft:-3/4

Die twee hellingen zijn negatieve reciproke van elkaar. Vrijwel alle loodrechte lijnen moeten negatieve wederzijdse hellingen hebben. De enige uitzondering doet zich voor wanneer een lijn die evenwijdig is aan de y-as een lijn snijdt met een helling nul. Het is gewoon zoals de dingen zijn.

We kunnen hellingen ook classificeren als "hoog" of "laag". Een "hoge" helling is er een die er heel, heel steil uitziet - zoals het oppervlak van een uitdagende rotswand. "Lage" of "ondiepe" hellingen zijn precies het tegenovergestelde.