
Wetenschap
Mobius-strips:zo eenvoudig te maken, zo moeilijk te doorgronden

De wiskunde van verder eenvoudig ogende objecten kan verrassend verwarrend zijn. Er is waarschijnlijk geen groter voorbeeld hiervan dan de Möbius-strip.
Het is een eenzijdig object dat kan worden gemaakt door simpelweg een stuk papier te draaien en de uiteinden met wat tape te verbinden. Als je de lus met je vinger zou volgen, zou je uiteindelijk precies teruggaan waar je begon, terwijl je het hele oppervlak van de lus tijdens de reis had aangeraakt. Deze eenvoudige creatie, de Möbius-strip, is fundamenteel voor het hele gebied van topologie en dient als een typisch voorbeeld van verschillende wiskundige principes.
Een van deze principes is niet-oriënteerbaarheid , wat het onvermogen is voor wiskundigen om coördinaten aan een object toe te wijzen, bijvoorbeeld omhoog of omlaag, of van links naar rechts. Dit principe heeft een aantal interessante resultaten, aangezien wetenschappers niet helemaal zeker weten of het universum oriënteerbaar is.
Dit levert een verbijsterend scenario op:als een raket met astronauten lang genoeg de ruimte in vloog en vervolgens terugkeerde, ervan uitgaande dat het universum niet-oriënteerbaar was, is het mogelijk dat alle astronauten aan boord omgekeerd terug zouden komen.
Met andere woorden, de astronauten zouden terugkomen als spiegelbeelden van hun vroegere zelf, volledig omgedraaid. Hun hart zou aan de rechterkant zijn in plaats van aan de linkerkant en ze kunnen linkshandig zijn in plaats van rechtshandig. Als een van de astronauten vóór de vlucht zijn rechterbeen had verloren, zou de astronaut bij terugkeer zijn linkerbeen missen. Dit is wat er gebeurt als je over een niet-oriënteerbaar oppervlak rijdt, zoals een Möbius-strook.
Terwijl hopelijk je geest wordt opgeblazen - in ieder geval een klein beetje - moeten we een stap terug doen. Wat is een Möbius-strip en hoe kan een object met zo'n complexe wiskunde worden gemaakt door simpelweg een stuk papier te draaien?
Inhoud
- De geschiedenis van de Möbiusstrook
- Praktisch gebruik van de Mobius Strip
- Hoe maak je een Möbius-strip aan?
De geschiedenis van de Möbiusstrook
De Möbius-strip (soms geschreven als "Mobius-strip") werd voor het eerst ontdekt in 1858 door een Duitse wiskundige genaamd August Möbius terwijl hij meetkundige theorieën deed. Hoewel Möbius grotendeels wordt toegeschreven aan de ontdekking (vandaar de naam van de strip), werd deze bijna gelijktijdig ontdekt door een wiskundige genaamd Johann Listing. Hij hield echter op met het publiceren van zijn werk en werd verslagen door August Möbius.
De strip zelf wordt eenvoudig gedefinieerd als een eenzijdig niet-oriënteerbaar oppervlak dat wordt gecreëerd door een halve draai aan een band toe te voegen. Möbius-strips kunnen elke band zijn met een oneven aantal halve slagen, waardoor de strip uiteindelijk maar één zijde heeft, en dus één rand.
Sinds zijn ontdekking heeft de eenzijdige strip een fascinatie voor kunstenaars en wiskundigen. De strip maakte zelfs M.C. Escher, leidend tot zijn beroemde werken, "Möbius Strip I&II".
De ontdekking van de Möbius-strook was ook fundamenteel voor de vorming van het gebied van wiskundige topologie, de studie van geometrische eigenschappen die onveranderd blijven als een object wordt vervormd of uitgerekt. Topologie is van vitaal belang voor bepaalde gebieden van wiskunde en natuurkunde, zoals differentiaalvergelijkingen en snaartheorie.
Volgens topografische principes is een mok bijvoorbeeld eigenlijk een donut. Wiskundige en kunstenaar Henry Segerman legt het het beste uit in een YouTube-video:"Als je een koffiemok neemt, kun je de plek waar de koffie naartoe gaat een beetje losmaken en kun je het handvat een beetje uitknijpen en uiteindelijk kun je het vervormen in [a] symmetrische ronde donutvorm." (Dit verklaart de grap dat een topoloog iemand is die het verschil niet kan zien tussen een donut en een koffiemok.)
Praktisch gebruik van de Mobius Strip
De Möbius-strip is meer dan alleen een geweldige wiskundige theorie:hij heeft een aantal coole praktische toepassingen, of het nu gaat om een leerhulpmiddel voor complexere objecten of in machines.
Omdat de Möbius-strip bijvoorbeeld fysiek eenzijdig is, zorgt het gebruik van Möbius-strips in transportbanden en andere toepassingen ervoor dat de band zelf gedurende zijn hele levensduur geen ongelijkmatige slijtage krijgt. Universitair hoofddocent NJ Wildberger van de School of Mathematics aan de Universiteit van New South Wales, Australië, legde tijdens een lezingenreeks uit dat er vaak een twist wordt toegevoegd aan aandrijfriemen in machines, "met opzet om de riem aan beide zijden gelijkmatig te dragen." De Möbius-strip is ook te zien in de architectuur, bijvoorbeeld de Wuchazi-brug in China.

Dr. Edward English Jr., wiskundeleraar op de middelbare school en voormalig optisch ingenieur, zegt dat toen hij voor het eerst hoorde over de Möbius-strip op de lagere school, zijn leraar hem er een liet maken met papier, waarbij hij de Möbius-strip in de lengte doorsneed, waardoor een langere strip met twee volledige wendingen.
"Geïntrigeerd zijn door en blootgesteld worden aan dit concept van twee 'toestanden' hielp me, denk ik, toen ik op/neer-spin van elektronen tegenkwam," zegt hij, verwijzend naar zijn Ph.D. studies. "Verschillende kwantummechanica-ideeën waren voor mij niet zulke vreemde concepten om te accepteren en te begrijpen, omdat de Möbius-strip me kennis liet maken met dergelijke mogelijkheden." Voor velen is de Möbius-strip de eerste kennismaking met complexe geometrie en wiskunde.
Hoe maak je een Möbius-strip aan?

Een Möbius-strip maken is ongelooflijk eenvoudig. Neem gewoon een stuk papier en knip het in een dunne strook, zeg een inch of 2 breed (2,5-5 centimeter). Als je die strook eenmaal hebt gesneden, draai je gewoon een van de uiteinden 180 graden of een halve draai. Neem vervolgens wat tape en verbind dat uiteinde met het andere uiteinde, zodat een ring ontstaat met een halve draai aan de binnenkant. Je houdt nu een Möbius-strip over!
U kunt de principes van deze vorm het beste observeren door uw vinger te nemen en langs de zijkanten van de strip te volgen. Uiteindelijk kom je helemaal rond de vorm en vind je je vinger terug waar hij begon.
Als je een Möbius-strook door het midden snijdt, over de volledige lengte, houd je één grotere lus over met vier halve slagen. Dit laat je met een gedraaide cirkelvorm, maar een die nog steeds twee kanten heeft. Het is deze dualiteit die Dr. English noemde, die hem hielp om complexere principes te begrijpen.
Dat is nou coolAls je een bagel snijdt langs het pad van een Möbius-strook, houd je twee aan elkaar verbonden bagelringen over. Niet alleen dat, maar het oppervlak van de snede zal groter zijn dan alleen het doormidden snijden van de bagel, zodat u meer roomkaas op de bagel kunt smeren om te eten.
 Magnesiumlegering als lichter alternatief voor aluminiumlegering
Magnesiumlegering als lichter alternatief voor aluminiumlegering Het toevoegen van een inert polymeer aan plastic zonnecellen zorgt voor een hoog rendement en eenvoudige productie
Het toevoegen van een inert polymeer aan plastic zonnecellen zorgt voor een hoog rendement en eenvoudige productie Hoe de tijd voor cellen te vertragen?
Hoe de tijd voor cellen te vertragen? Nieuwe synthetische route voor productie van biobrandstoffen
Nieuwe synthetische route voor productie van biobrandstoffen 3D-printen elektrisch ondersteund, op parelmoer geïnspireerde structuren met zelfgevoelige mogelijkheden
3D-printen elektrisch ondersteund, op parelmoer geïnspireerde structuren met zelfgevoelige mogelijkheden
 Biotische en abiotische factoren in het savannegrasland
Biotische en abiotische factoren in het savannegrasland Klimaatverandering en de ineenstorting van Angkor Wat
Klimaatverandering en de ineenstorting van Angkor Wat EU geeft laatste waarschuwing aan Groot-Brittannië, Frankrijk over luchtvervuiling
EU geeft laatste waarschuwing aan Groot-Brittannië, Frankrijk over luchtvervuiling Parijs experimenteert met zelfrijdende bussen (update)
Parijs experimenteert met zelfrijdende bussen (update) Studies onderzoeken de rol van bodembedekkers bij het onderdrukken van glyfosaatresistent paardenkruid
Studies onderzoeken de rol van bodembedekkers bij het onderdrukken van glyfosaatresistent paardenkruid
Hoofdlijnen
- Microbieel moordmysterie opgelost
- Wat zijn de twee belangrijkste functies van nucleïnezuur in levende wezens?
Nucleïnezuren zijn kleine stukjes materie met grote rollen om te spelen. Genoemd naar hun locatie - de kern - deze zuren dragen informatie die cellen helpt bij het maken va
- Ontdekking van orgaanontwikkeling kan strijd tegen kanker stimuleren
- Wetenschappers bewerken vlindervleugelvlekken en strepen
- De evolutie van slijm:hoe zijn we aan al dit slijm gekomen?
- Hoe antidepressiva werken
- Delen van een dierencel voor kinderen
- Hoe een DNA-model te labelen
- Waarom planten spruiten vormen in het donker
- Nanometers converteren naar Joules

- Kwantumonderzoek verenigt twee ideeën en biedt een alternatieve route naar topologische supergeleiding

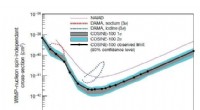
- COSINE-100-experiment onderzoekt mysterie van donkere materie
- Onderzoekers rapporteren nauwkeurigere meting van neutronen

- Natuurkundigen ontdekken nieuw type spingolven

 Regen belemmert reddingspogingen na dodelijke overstromingen in Japan
Regen belemmert reddingspogingen na dodelijke overstromingen in Japan Onderzoekers observeren interband collectieve excitaties in gedraaid dubbellaags grafeen
Onderzoekers observeren interband collectieve excitaties in gedraaid dubbellaags grafeen  Gezondheidssector geeft blockchain gloeiende prognose
Gezondheidssector geeft blockchain gloeiende prognose Zonnepanelen vervangen asfalt op een snelweg - hier zijn de resultaten
Zonnepanelen vervangen asfalt op een snelweg - hier zijn de resultaten Ingenieurs 3D print zacht, rubberachtige hersenimplantaten
Ingenieurs 3D print zacht, rubberachtige hersenimplantaten Mechanisme voor hMTH1s brede substraatspecificiteit onthuld
Mechanisme voor hMTH1s brede substraatspecificiteit onthuld Artsen zeggen dat de meeste statistieken van uw Apple Watch, Fitbit is niet nuttig voor hen
Artsen zeggen dat de meeste statistieken van uw Apple Watch, Fitbit is niet nuttig voor hen Verhoogde wereldwijde sterfte in verband met blootstelling aan arseen in diëten op basis van rijst
Verhoogde wereldwijde sterfte in verband met blootstelling aan arseen in diëten op basis van rijst
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

