Wetenschap
Ontdekking van een hybride huidtopologisch effect veroorzaakt door winst en verlies
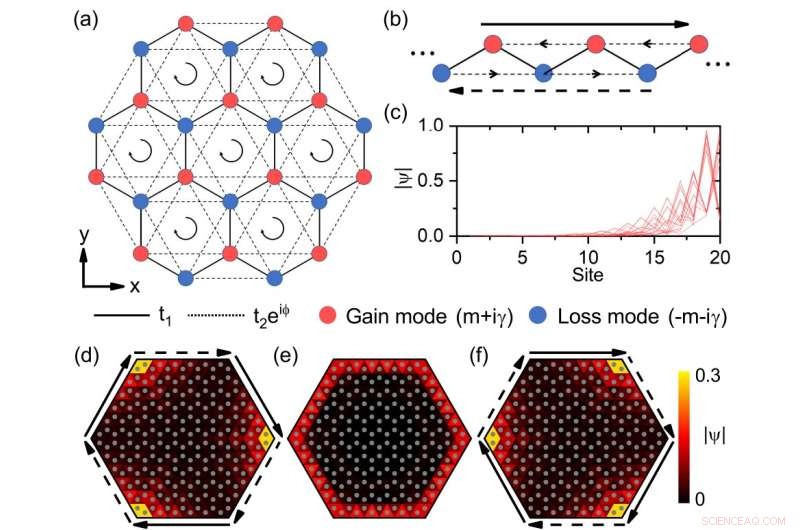
Fig. 1 Hybride huidtopologische modi in niet-Hermitiaans Haldane-model. (a) Schema van het niet-Hermitiaanse rooster. De rode (blauwe) cirkels geven locaties aan met tegengestelde massatermen +(m+iγ). (b) Zigzagrand van het honingraatrooster als een 1D-keten, die een niet-Hermitiaans huideffect heeft met winst en verlies ter plaatse. De lange ononderbroken (gestippelde) pijl geeft de chirale randstroom aan langs (tegenover) de gelokaliseerde richting [vergelijkbaar in (d) en (f)]. De zwarte pijlen in (a) en middelste pijlen in (b) geven de richtingen aan van de volgende-dichtstbijzijnde-buurkoppelingen t2 e iφ . (c) Profiel van alle eigenmodes voor de 1D-keten in (b) met 20 sites. De winst en het verlies ter plaatse zijn γ=3. (d)-(f) De chirale randmodus voor γ=0 (e) wordt huidtopologische modi voor γ=-0.6 (d) en γ=0.6 (f) met verschillende gelokaliseerde richtingen. Elke driehoek met een grijze cirkel geeft een site aan. Hier plant de chirale randmodus zich met de klok mee voort. Krediet:Tsinghua University
Onlangs hebben universitair hoofddocent Yong-Chun Liu van de afdeling Natuurkunde en anderen het hybride huidtopologische effect ontdekt dat wordt veroorzaakt door winst en verlies en de pariteitsfase-overgang tussen huidtopologische modi. De onderzoeksresultaten zijn gepubliceerd in Physical Review Letters onder de titel "Gain-loss-geïnduceerd hybride huid-topologisch effect."
Niet-Hermitische systemen zijn open systemen die kunnen worden beschreven door niet-Hermitische Hamiltonianen. Er zijn veel nieuwe eigenschappen in niet-Hermitische systemen, waaronder het niet-Hermitische huideffect. In dit effect worden alle eigentoestanden van een topologisch systeem (inclusief bulktoestanden en randtoestanden) gelokaliseerd op een van de systeemgrenzen en wordt de conventionele bulk-edge-correspondentie afgebroken. Er zijn hoofdzakelijk twee manieren om niet-Hermitiaanse systemen te realiseren:de ene gebruikt niet-wederkerige koppelingen en de andere gebruikt winst en verlies.
In het geval van niet-wederkerige koppelingen komt de niet-Hermiticiteit voort uit de niet-Hermitiaanse aard van de interactie tussen verschillende roosterplaatsen. De energie-uitwisseling tussen de roosterplaatsen is asymmetrisch, dus er is een netto energiestroom in één richting en alle energie wordt uiteindelijk verzameld op de grens. De niet-wederkerige systemen vertonen dus het skin-effect. In het geval van winst-verlies, komt de niet-hermiticiteit voort uit de winst en het verlies op elke roosterplaats, wat gelijk staat aan het toevoegen van denkbeeldige energie ter plaatse aan elke roosterplaats. Dit soort niet-Hermitiaans systeem leidt niet altijd tot het skin-effect. In realistische systemen zijn niet-wederkerige koppelingen meestal moeilijk te bereiken, maar dissipatie is wijdverbreid en gespreide dissipatiedissipatie is gelijk aan winst en verlies. Daarom is het van groot belang om het skin-effect in niet-Hermitiaanse systemen met winstverlies te bestuderen.
Ze vonden het hybride huidtopologische effect dat wordt veroorzaakt door winst en verlies in tweedimensionale systemen. Dit soort skin-effect is selectief, d.w.z. de bulktoestanden en de randtoestanden hebben verschillend gedrag. De bulktoestanden worden niet beïnvloed door het skin-effect en blijven verlengd, terwijl de randtoestanden skin-effect vertonen en verder naar hoeken zijn gelokaliseerd. Dit hybride fenomeen van huideffect en topologisch effect toont de unieke eigenschappen van niet-Hermitische topologische systemen, die geen Hermitische of niet-topologische analogen hebben.
Als specifiek voorbeeld beschouwden ze het niet-Hermitiaanse Haldane-model met winst en verlies [Fig. 1 (a)]. In het Haldane-model worden de topologische randtoestanden verkregen door ter plaatse energie en lokale magnetische flux te introduceren. Het is een van de twee belangrijke modellen om het kwantum afwijkende Hall-effect in de fysica van de gecondenseerde materie te realiseren. Ze ontdekten dat als gespreide winst en verlies worden geïntroduceerd in de dichtstbijzijnde buurlocaties in het Haldane-model, de topologische randmodi van het systeem het skin-effect zullen vertonen en gelokaliseerd zijn in de hoeken, terwijl de bulkmodi niet worden beïnvloed. Het onthult dus een hybride huidtopologisch effect.
Door alleen de roosterplaatsen aan de randen te analyseren, kan dit tweede-orde skin-topologische effect worden vereenvoudigd tot het eerste-orde skin-effect aan de randen. In het vereenvoudigde eendimensionale model zijn er chirale randstromen als gevolg van de niet-lokale magnetische flux die wordt geïntroduceerd door de complexe naast-dichtstbijzijnde-buurkoppelingen. Ze zijn equivalent aan niet-wederkerige koppelingen, dus het systeem vertoont het eerste-orde skin-effect [Fig. 1 (b)—(c)]. Integendeel, er is alleen lokale flux, en de niet-wederkerigheid heft in het grootste deel van het systeem op. De bulkmodi worden dus niet beïnvloed door het skin-effect. Door de versterking en het verlies van het systeem aan te passen, kan de richting van de randstromen worden gewijzigd om de richting van het huidtopologische effect te regelen [Fig. 1 (d)—(f)].
Ze verkregen verder de relatie tussen de pariteits-tijd (PT) symmetrieën van het systeem en het hybride huid-topologische effect. Bij het kiezen van de open randvoorwaarde en de periodieke randvoorwaarde in verschillende richtingen, vertoont het systeem verschillende soorten PT-symmetrieën voor verschillende soorten randen. De globale PT-symmetrie die elke modus die in de ene grens is gelokaliseerd in de andere grens in kaart brengt, sluit de opkomst van het hybride huidtopologische effect uit, terwijl de lokale PT-symmetrie met mapping binnen elke subcel het bestaan van het hybride huidtopologische effect mogelijk maakt.
Daarom biedt de analyse van PT-symmetrieën van het systeem een eenvoudige en effectieve manier om te beoordelen of er een hybride huidtopologisch effect is. In het bijzonder ontdekten ze dat wanneer de winst en het verlies in het systeem toenemen, de PT-faseovergang zal plaatsvinden tussen de huidtopologische modi, vergezeld van het verschijnen van uitzonderlijke punten (EP's). Wanneer de PT-symmetrie wordt verbroken, zijn de eigenenergieën van de huidtopologische modi niet langer reëel en worden de verdelingen van de overeenkomstige eigenmodi PT-asymmetrisch.
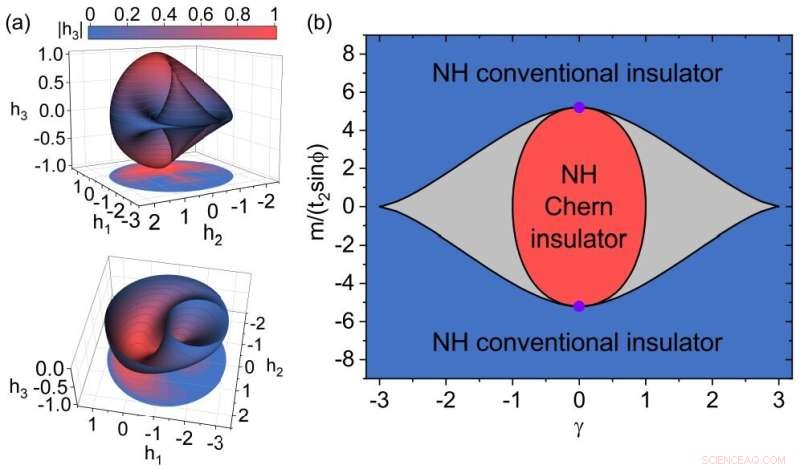
Fig. 2 The topology and phase diagram of the non-Hermitian Haldane model. (a) The surface S mapped from the first Brillouin zone, i.e., mapping from (kx , ky ) to (h1 , h2 , h3 ). The color map represents the magnitude of h3 . The density map below is the projection of the surface. The bottom figure is half of the top figure for h3 <0. (b) The phase diagram. The red area is the non-Hermitian Chern insulator phase where C=1. The blue area is the non-Hermitian conventional insulator phase where C=0. The gray area is a gapless phase with EPs between two bulk bands. The black curves are phase boundaries. The purple points indicate the Hermitian phase boundary with the emergence of Dirac points. Credit:Tsinghua University
In addition, they studied the Chern numbers in the non-Hermitian system and obtained the phase diagram. They provided intuitionistic geometric meanings of the Chern numbers as topological invariants. As shown in Fig. 2(a), the two-dimensional Brillouin zone of the system can be mapped to a closed spherical surface S in the three-dimensional space, and the gap-closing points of the system form a circle L in the three-dimensional space. When the surface S encloses the circle L, the system is at the non-Hermitian Chern insulator phase, and the Chern number is 1, corresponding to the red region in Fig. 2(b). When the circle L is outside the surface S, the system is at the non-Hermitian conventional insulator phase, and the Chen number is 0, corresponding to the blue area in Fig. 2 (b). In the gray area in Fig. 2 (b), the system band gap is closed at six EPs.
The conclusion of this work is also applicable to the system with no gain and only pure dissipation. Dissipation is common in many physical systems, such as optical systems, atomic systems, and optomechanical systems. This work paves the way to realize non-Hermitian topological effect by gain and loss and study PT phase transition in higher-dimensional systems. It also provides attractive insights for potential applications in topological optics. + Verder verkennen
An approach for constructing non-Hermitian topological invariants in real space
 Nieuwe inzichten in het toxine achter tetanus
Nieuwe inzichten in het toxine achter tetanus Gebruik van Polyvinyl Acetate
Gebruik van Polyvinyl Acetate Zonlicht kan worden gebruikt om verontreinigende stoffen in water uit te roeien
Zonlicht kan worden gebruikt om verontreinigende stoffen in water uit te roeien Kennis opbouwen van veranderingen in de uraniumchemie
Kennis opbouwen van veranderingen in de uraniumchemie Wat is Variable Valency?
Wat is Variable Valency?
Elektronen bestaan in banen rond een atoomkern. Hoe hoger het aantal banen, hoe groter de afstand van de elektronen tot de kern. Atomen proberen een stabiele toestand te bereiken vergelijkbaar met die van de edelgassen of
 FOTO'S:Scènes onder de middernachtzon in het noordpoolgebied
FOTO'S:Scènes onder de middernachtzon in het noordpoolgebied Wat is de toekomst van bioplastics?
Wat is de toekomst van bioplastics?  Nieuwe verweringsanalyse volgt nauwkeurig de geochemische flux onder het aardoppervlak
Nieuwe verweringsanalyse volgt nauwkeurig de geochemische flux onder het aardoppervlak Geavanceerde modelleringstechnieken kunnen de manier waarop steden omgaan met overstromingen verbeteren
Geavanceerde modelleringstechnieken kunnen de manier waarop steden omgaan met overstromingen verbeteren Duurzame ontwikkelingsdoelen hebben een laatste zetje nodig met nog maar 10 jaar te gaan
Duurzame ontwikkelingsdoelen hebben een laatste zetje nodig met nog maar 10 jaar te gaan
Hoofdlijnen
- Een bouwsteen voor leverfitness op oudere leeftijd
- Gymnospermen: definitie, levenscyclus, typen en voorbeelden
- Geometrie speelt een belangrijke rol in hoe cellen zich gedragen, onderzoekers rapporteren
- Verdringing in de huid:stamcellen voelen buurtdichtheid om beslissingen te nemen
- Beoordelingskader voor de instandhouding en het beheer van peulvruchtenplanten in Oost-Afrika aan de kust
- Geen bewijs dat het onthoornen van zwarte neushoorns een negatieve invloed heeft op de voortplanting of overleving van de soort, studievondsten
- Nieuwe insectensoort bootst dode bladeren na voor camouflage
- Een Chromosome-diagram interpreteren
- Wat is de elektrische impuls die een axon naar beneden beweegt?
 Snel, betrouwbare test voor besmetting met micro-organismen
Snel, betrouwbare test voor besmetting met micro-organismen Nieuwe stoffenbibliotheek om het zoeken naar actieve stoffen te versnellen
Nieuwe stoffenbibliotheek om het zoeken naar actieve stoffen te versnellen Eenzaamheid blijkt hoog te zijn in openbare woongemeenschappen voor senioren
Eenzaamheid blijkt hoog te zijn in openbare woongemeenschappen voor senioren Digitale marketing verbetert de naleving van productterugroepacties, een nieuw hulpmiddel bieden om de veiligheid van de consument te verbeteren
Digitale marketing verbetert de naleving van productterugroepacties, een nieuw hulpmiddel bieden om de veiligheid van de consument te verbeteren Folie versus Mylar
Folie versus Mylar Explosie in Beiroet:de ramp was uitzonderlijk, maar de gebeurtenissen die eraan voorafgingen niet, zeggen onderzoekers
Explosie in Beiroet:de ramp was uitzonderlijk, maar de gebeurtenissen die eraan voorafgingen niet, zeggen onderzoekers Verband tussen continentaal uiteenvallen, vulkanische koolstofemissies en evolutie
Verband tussen continentaal uiteenvallen, vulkanische koolstofemissies en evolutie Hoe inheemse kennis de moderne wetenschap en technologie vooruit helpt
Hoe inheemse kennis de moderne wetenschap en technologie vooruit helpt
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com