
Wetenschap
Onderzoekers vinden een betere machtswet die aardbevingen voorspelt, aderen, bankrekeningen
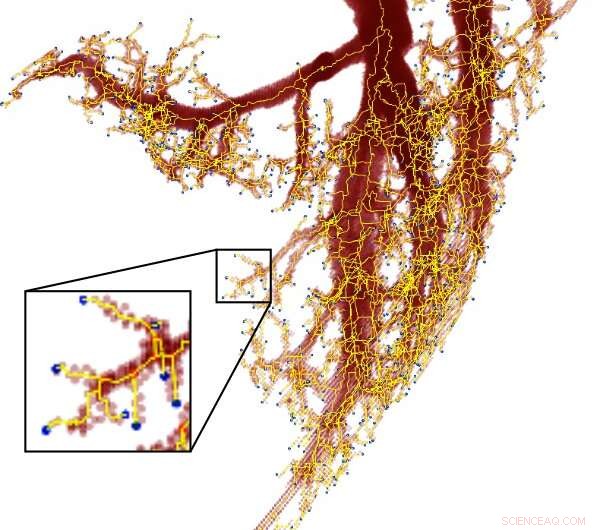
Omdat aderen zich in ongeveer evenredige delen vertakken, ze worden ook als een fractal beschouwd. Krediet:met dank aan afbeelding/Mitchell Newberry
Gigantische aardbevingen en extreme rijkdom lijken misschien niet veel gemeen te hebben, maar de frequentie waarmee de "Big One" San Francisco zal raken en hoe vaak iemand zoveel geld zal verdienen als Bill Gates, kunnen beide worden voorspeld met een statistische meting die een machtswet-exponent wordt genoemd.
Voor de vorige eeuw, onderzoekers hebben een zogenaamde machtswet gebruikt om bepaalde soorten gebeurtenissen te voorspellen, inclusief hoe vaak aardbevingen op bepaalde punten op de schaal van Richter zullen voorkomen. Maar een onderzoeker van de Universiteit van Michigan merkte op dat deze machtswet niet in alle omstandigheden past.
Mitchell Newberry, een fellow uit Michigan en assistent-professor aan het UM Center for the Study of Complex Systems, suggereert een aanpassing van de machtswet die rekening zou houden met gebeurtenissen die in vaste verhoudingen toenemen of afnemen, bijvoorbeeld, wanneer een manager ongeveer 20 procent meer verdient dan zijn of haar werknemer.
Deze aanpassingen zijn van invloed op de schatting van de kans op aardbevingen, het aantal haarvaten in het menselijk lichaam, en de grootte van megasteden en zonnevlammen. En ze kunnen herzien wanneer ze de volgende Big One kunnen verwachten.
Wanneer wetenschappers zoiets als de waarschijnlijkheid van extreme rijkdom in een grafiek plotten, de curve is een vloeiende lijn. Dat komt omdat mensen elk bedrag op hun bankrekening kunnen hebben.
"De gladheid van deze curve betekent dat elke waarde mogelijk is, ' zei Newberry. 'Ik zou net zo gemakkelijk een cent meer kunnen verdienen als een cent minder.'
Dat is niet precies het geval bij gebeurtenissen zoals aardbevingen vanwege de manier waarop ze worden geregistreerd op de schaal van Richter. De Richter-magnitude van aardbevingen neemt toe of af in stappen van 0,1, exponentieel. Een aardbeving met een kracht van 3,1 is 1,26 keer zo krachtig als een aardbeving met een kracht van 3,0. dus niet elke waarde is mogelijk op de schaal. De schaal van Richter is een voorbeeld van een concept dat "zelfgelijkenis, " of wanneer een gebeurtenis of ding is gemaakt van proportioneel kleinere kopieën van zichzelf.
Zelfgelijkenis in de natuur kun je zien als de vertakking van nerven in een blad, of in geometrie als passende driehoeken binnen grotere driehoeken van dezelfde vorm, een Sierpinski-driehoek genoemd. Dus, om rekening te houden met gebeurtenissen die in exacte proporties veranderen, Newberry en zijn co-auteur Van Savage van de Universiteit van Californië, Los Angeles, construeerde de discrete machtswet.

De Koch-curve herhaalt zich oneindig, zelfgelijkenis vertonen. Krediet:Wikimedia-gebruiker Leofun01
In deze machtswetvergelijkingen, de exponent in de vergelijking is de variabele waarvoor wetenschappers een oplossing zoeken. Bij aardbevingen, die exponent, de Gutenberg-Richter b-waarde genoemd, werd voor het eerst gemeten in 1944 en geeft aan hoe vaak een aardbeving van een bepaalde sterkte waarschijnlijk zal voorkomen. De discrete machtswet van Newberry produceerde een correctie van 11,7% ten opzichte van schattingen op basis van de continue machtswet, de exponent dichter bij de historische frequentie van grote aardbevingen brengen. Zelfs een correctie van 5% vertaalt zich in een meer dan tweevoudig verschil in wanneer de volgende gigantische aardbeving kan worden verwacht.
"Al 100 jaar mensen hebben gesproken over ongeveer één soort verdeling van de machtswetten. Het is de machtswetverdeling van rijkdom en aardbevingen, " zei Newberry. "Alleen nu, we documenteren deze discrete schalen. In plaats van een vloeiende curve, onze machtswet ziet eruit als een oneindige trap."
Newberry merkte de fout in de continue machtswet op in zijn studie van de fysica van de bloedsomloop. De bloedsomloop begint met één groot bloedvat:de aorta. Naarmate de aorta zich splitst in verschillende takken - de halsslagader en de subclavia - neemt elke nieuwe tak in diameter met ongeveer tweederde af.
Hij gebruikte de continue machtswet om de afmetingen van bloedvaten te schatten terwijl ze zich blijven vertakken. Maar de machtswet leverde afmetingen van bloedvaten op die niet konden voorkomen. Het gaf aan dat een bloedvat misschien maar iets kleiner is dan de stam waaruit het vertakt in plaats van ongeveer tweederde van de grootte van die stam.
"Met behulp van de continue machtswet, we kregen net antwoorden waarvan we wisten dat ze fout waren, " zei Newberry. "Door te debuggen wat mislukte, we kwamen erachter dat deze verdeling de veronderstelling maakt dat elke bloedvatgrootte even plausibel is. We weten dat voor echte vasculatuur, dat is niet het geval."
Dus Newberry heeft de machtswet omgekeerd. Door naar bloedvaten te kijken, Newberry kon de machtswet-exponent afleiden uit twee constanten:hoeveel vertakkingen op elke kruising - twee - en hoeveel kleiner elke vertakking is ten opzichte van de stam. Vatmaten meten bij elke divisie, Newberry kon de verdeling van de bloedvaten oplossen.
"Er is een middenweg tussen een continue machtswet en de discrete machtswet, " zei Newberry. "In de discrete machtswet, alles is in perfect strakke proporties ingedeeld, van de hoogste schaal tot het oneindig kleine. In de continue machtswet, alles is perfect willekeurig ingedeeld. Bijna alles wat in werkelijkheid op zichzelf lijkt, is een mix van deze twee."
De studie van Newberry is gepubliceerd in het tijdschrift Fysieke beoordelingsbrieven .
 Wetenschappers vinden een fluctuerende stijgende trend van open landbouwstroverbranding in Noordoost-China
Wetenschappers vinden een fluctuerende stijgende trend van open landbouwstroverbranding in Noordoost-China Effectief verwijderen van kooldioxide uit de atmosfeer
Effectief verwijderen van kooldioxide uit de atmosfeer Soorten bomen, gras en struiken in de savanne
Soorten bomen, gras en struiken in de savanne  Visgedrag Wetenschap Eerlijke ideeën
Visgedrag Wetenschap Eerlijke ideeën  Klimaatverandering vergroot migratie ten koste van de armen
Klimaatverandering vergroot migratie ten koste van de armen
Hoofdlijnen
- Wetenschappers werken aan een omkeerbare vorm van genbewerking
- Feiten over Prokaryotic
- Evolutionaire relaties tussen prokaryoten en eukaryoten
- Ontmoet Afrika's vogelmeester van vocale imitatie
- Dierenartsen voeren de eerste bekende hersenoperatie uit om hydrocephalus bij pelsrobben te behandelen
- Natuurbeschermingsgroep zegt dat Japan helpt bij illegale ivoorhandel (update)
- 7 soorten bindweefsel
- Een niet-verslavende opioïde pijnstiller zonder bijwerkingen
- Hoe kan een mutatie in DNA invloed hebben op eiwitsynthese?
- Natuurkundigen bepalen de beloning tussen snelheid en entropie

- Belangrijke ontdekking bij het beheersen van kwantumtoestanden van afzonderlijke atomen

- Een kristal gemaakt van elektronen

- Chiraal nulgeluid gevonden in Weyl-halfmetalen
- Een fotonische curveball heeft voorbeelden uit de echte wereld in voetbal, basketbal

 Discriminerende diëten van vleesetende dinosaurussen
Discriminerende diëten van vleesetende dinosaurussen Vier tips om sneller bediend te worden in de kroeg - nieuw onderzoek
Vier tips om sneller bediend te worden in de kroeg - nieuw onderzoek Hoe nanowetenschap onze gezondheid en ons leven de komende jaren zal verbeteren
Hoe nanowetenschap onze gezondheid en ons leven de komende jaren zal verbeteren New York zou plastic schuimcontainers over de hele staat kunnen verbieden onder het voorstel van Cuomo
New York zou plastic schuimcontainers over de hele staat kunnen verbieden onder het voorstel van Cuomo Wat is 's werelds langste hangbrug?
Wat is 's werelds langste hangbrug?  Japan tyfoon gronden vluchten, verwondt drie
Japan tyfoon gronden vluchten, verwondt drie Bedrijven kunnen vertrouwen opbouwen bij consumenten door gegevens over hun praktijken te ontsluiten
Bedrijven kunnen vertrouwen opbouwen bij consumenten door gegevens over hun praktijken te ontsluiten Levende sensor kan mogelijk milieurampen door brandstofverspilling voorkomen
Levende sensor kan mogelijk milieurampen door brandstofverspilling voorkomen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway | French | Italian |

-
Wetenschap © https://nl.scienceaq.com

