
Wetenschap
Onderzoekers bieden nieuwe natuurkundige regel om mechanische belasting te vinden
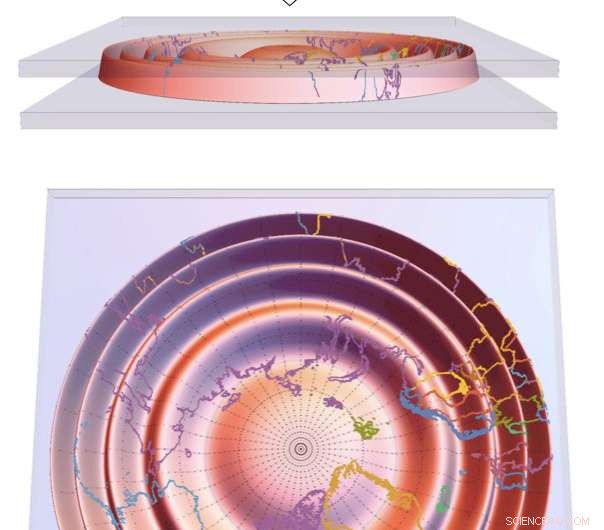
Dit schema laat zien wat er gebeurt als een gebogen elastische schaal, hier afgebeeld als een wereldbol, wordt door opsluiting gedwongen om van bolvormig naar vlak te veranderen. Als het genoeg kreukt, de schaal kan bijna plat worden zonder uit te rekken. De onderste afbeelding laat zien dat de afstandsvervorming die wordt geïntroduceerd bij het platdrukken van een wereldbol - in vergelijking met een vooraf geplette kaart - willekeurig kleiner kan zijn naarmate de schaal dunner en buigzamer wordt. Deze oplossing, ontwikkeld door UMass Amherst-onderzoekers, verzoent kernprincipes en schijnbaar tegenstrijdige principes van geometrie en mechanica. Krediet:UMass Amherst/G. Grason
Een natuurkundig probleem aanpakken dat teruggaat tot Galileo, drie Amherst-onderzoekers van de University of Massachusetts stellen deze week een nieuwe benadering voor van de theorie over hoe dunne vellen kunnen worden gedwongen om zich aan te passen aan "geometrisch onverenigbare" vormen - denk aan het inpakken van een basketbal - die gebaseerd is op het samenweven van twee fundamentele ideeën van geometrie en mechanica die lang als onverenigbaar werden beschouwd.
Theoretisch natuurkundige Benny Davidovitch, polymeerwetenschapper Greg Grason en promovendus Yiwei Sun, schrijven in Proceedings van de National Academy of Sciences , suggereren en demonstreren via numerieke simulaties dat van nature vlakke platen die gedwongen worden hun kromming te veranderen, de geometrisch vereiste spanning kunnen opvangen door microscopische rimpels te ontwikkelen die de plaat buigen in plaats van uit te rekken tot het breekpunt, een oplossing die minder energie kost, ook.
Deze vooruitgang is belangrijk omdat biotechnologen in toenemende mate proberen het spanningsniveau te beheersen dat wordt aangetroffen in dunne films die voldoen aan complexe, gebogen en 3D-vormen van het menselijk lichaam, bijvoorbeeld, in flexibele en draagbare sensoren voor gepersonaliseerde gezondheidsmonitoring, ze leggen uit. Veel van deze apparaten zijn afhankelijk van de elektrische eigenschappen van de film, waarvan is aangetoond dat deze zeer kwetsbaar is voor uitrekken, maar die enige buiging kan verdragen.
Het nieuwe concept is er een van "dicht genoeg, " zegt Davidovitch - afwijkingen die gepaard gaan met buigen zijn zo klein dat in praktische termen, ze kosten bijna geen energie. "Door efficiënte strategieën aan te bieden om de stam te beheren, voorspellen en beheersen, we bieden een nieuw kwantitatief hulpmiddel dat nuttig is voor mensen die de krachten voorspellen die nodig zijn om nanoscopische dunne vellen en schalen op substraten van verschillende vormen te embosseren of te wikkelen, ’ stellen ze.
Hij voegt toe, "Ons werk laat zien dat door kleine rimpels in de verpakking toe te staan, de benodigde hoeveelheid stretching neemt drastisch af. Voor een extreem dunne wikkel zoals die tegenwoordig in laboratoria verkrijgbaar is, het uitrekken kan bijna volledig worden geëlimineerd."
Grason wijst erop, "Ons theoretisch raamwerk biedt een eenvoudig en aanpasbaar hulpmiddel om te begrijpen hoe te controleren en te manipuleren, en idealiter te optimaliseren, het spanningsniveau dat een bepaalde geometrie op een dergelijk apparaat legt, en daardoor de prestaties te verbeteren."
Davidovitch zegt dat er twee soorten wetenschappers zijn die geïnteresseerd zijn in dit al lang bestaande probleem:iemand die minder gemotiveerd is door praktische zaken dan door hoe de natuurwetten van toepassing zijn. Deze denkers zijn bekend met "Galileo's balk, " een mechanisch / natuurkundig probleem waarbij een balk werd voorgesteld die uit een stenen muur steekt en die zal buigen of vervormen wanneer er gewicht aan wordt toegevoegd, merkt hij op. Het voorspellen van de krachten en de belasting ervan vormde een al lang bestaande puzzel.
Galileo heeft niet opgelost hoeveel de straal zal vervormen of hoe dat te voorspellen, hij merkt op, maar dit probleem met betrekking tot spanning werd later onderzocht en gedefinieerd door nieuwe benaderingen van de geometrie van continue objecten door de Duitse wiskundige en natuurkundige Carl Friedrich Gauss. Natuurkundigen en wiskundigen "hebben er door de eeuwen heen veel intellectuele activiteit op gericht, ' zegt Davidovitch.
Na Galileo, Davidovitch zeg, De Zwitserse wiskundige Leonhard Euler ontwikkelde de "elasticatheorie, " die stelt dat besloten voorwerpen knikken om spanning te voorkomen, dat is, enige verandering in lengte. Euler toonde aan dat onder bijzondere omstandigheden een situatie kan ontstaan waarin absoluut niet gestrekt wordt, maar niet in het algemene type opsluiting gedefinieerd door de geometrische beperkingen van Gauss, hij voegt toe.
De nieuwe tool van het UMass Amherst-team laat zien - wanneer een beperking niet perfect kan worden bevredigd, maar bijna tevreden - hoe de fysieke staat of vorm te vinden die het beste past. "Het is een nieuwe tak van variatierekening, " zegt Davidovitch. "Het enige wat ik moet doen is de kromming minimaliseren die bijna alle rekken elimineert, en het laat me degene vinden met de kleinst mogelijke buigenergie."
Ze stellen een nieuw principe voor, de Gauss-Euler elastica, dat de twee hoekstenen van klassieke mechanica en geometrie verzoent die eerder door de werken van Euler en Gauss werden gedefinieerd. Ze roepen een nieuw regime van oplossingen op van de complexe morfologieën van dunne lichamen, een probleem van intense recente interesse van biofysica en materiaalkunde tot toegepaste wiskunde, merkt Grason op.
Hij herinnert zich, "Toen we voor het eerst met deze onderzoekslijn begonnen, we konden ons niet voorstellen hoe het zou aflopen. We probeerden dit probleem niet op te lossen." Maar promovendus Sun, het uitvoeren van enkele computersimulaties, kwam met resultaten die de naïeve aannames tartten dat opsluiting meer energie kost om uit te rekken dan om het laken te buigen. Formules die hij en Grason voorstelden waren "onmogelijk, "Davidovitch zegt, "ze leken fundamentele geometrische stellingen te schenden."
Ze zaten twee jaar vast, totdat ze zich de straal van Galileo herinnerden, wat Davidovitch een ‘gedachtentegenspraak’ noemt, " waardoor de vraag opnieuw werd geformuleerd. Het was "zeer bevredigend" om een nieuw conceptueel hulpmiddel voor het probleem te brengen dat voorheen niet beschikbaar was, hij zegt. Grason voegt toe, "Het is geweldig om een antwoord te hebben op waarom onze eerste simulaties zich zo raar gedroegen, natuurlijk. Maar uiteindelijk leidt het ons ertoe de vraag beter te begrijpen, en hoe het een veel bredere klasse van problemen op een nieuwe manier aanpakt. Ja, dit geeft een goed gevoel."
 Escherichia coli-bacteriën kapen koper, voed je ermee
Escherichia coli-bacteriën kapen koper, voed je ermee Stabiliserende zwavelkathode door enkelvoudig Li-ionkanaalpolymeerbindmiddel
Stabiliserende zwavelkathode door enkelvoudig Li-ionkanaalpolymeerbindmiddel Hittebestendige enzymen zouden meer kosteneffectieve medicijnen kunnen produceren
Hittebestendige enzymen zouden meer kosteneffectieve medicijnen kunnen produceren Stroomafwaartse signalering:Cilia laten ectosomen vrij om belangrijke berichten in de nier af te leveren
Stroomafwaartse signalering:Cilia laten ectosomen vrij om belangrijke berichten in de nier af te leveren Vastestofelektrolyt met lithium-iongeleidbaarheid vergelijkbaar met vloeibare elektrolyten
Vastestofelektrolyt met lithium-iongeleidbaarheid vergelijkbaar met vloeibare elektrolyten
 Microplastics zijn niet alleen een probleem voor de oceanen
Microplastics zijn niet alleen een probleem voor de oceanen Greenpeace vindt koraalrif in boorgebied Totals Amazon
Greenpeace vindt koraalrif in boorgebied Totals Amazon Bericht over kokend water opgeheven uit de stad Texas waar microben werden gevonden
Bericht over kokend water opgeheven uit de stad Texas waar microben werden gevonden Slow recycler Turkije zoekt beter gebruik voor zijn afval
Slow recycler Turkije zoekt beter gebruik voor zijn afval Bijna een op de drie mensen wereldwijd zal in 2030 nog steeds voornamelijk vervuilende kookbrandstoffen gebruiken
Bijna een op de drie mensen wereldwijd zal in 2030 nog steeds voornamelijk vervuilende kookbrandstoffen gebruiken
Hoofdlijnen
- Wat zijn de belangrijkste functionele kenmerken van alle organismen?
- Hoe slaapwandelen werkt
- Wat is een markermolecuul?
- Noordelijke maïsbladziekte-genen geïdentificeerd in nieuwe studie
- Biologen ontdekken tastzin van bacteriën
- Het verschil tussen orthologe en paraloge genen
- Voor een gestreepte mangoest in het noorden van Botswana, communiceren met familie kan dodelijk zijn
- Rechtbank vindt het goed om een soort uil te doden om het effect op andere uilen te zien
- Nieuwe strategie zou bestaande medicijnen in staat kunnen stellen bacteriën te doden die chronische infecties veroorzaken
- Golf van de toekomst:Terahertz zorgt voor een nieuwe manier om door materie te kijken

- Nieuwe neutronenbron in Canada zou innovatie stimuleren, medische behandelingen

- Team verbetert polaire direct drive fusie-neutronenbronnen voor gebruik in laserexperimenten

- Natuurkundigen onderzoeken toename homerun

- Voordelen en nadelen van het bouwen van dammen

 Afstandsonderwijs vormt een uitdaging voor sommige gezinnen van kinderen met een handicap
Afstandsonderwijs vormt een uitdaging voor sommige gezinnen van kinderen met een handicap Rechtbank in Tokio wijst verzoek om borgtocht ex-Nissan-chef Ghosn af
Rechtbank in Tokio wijst verzoek om borgtocht ex-Nissan-chef Ghosn af De uitstoot van lachgas 300 keer krachtiger dan koolstofdioxide brengt de toekomst van de aarde in gevaar
De uitstoot van lachgas 300 keer krachtiger dan koolstofdioxide brengt de toekomst van de aarde in gevaar Overstromingen, stormvloed kan net zo verwoestend zijn als de wind van een orkaan
Overstromingen, stormvloed kan net zo verwoestend zijn als de wind van een orkaan Oncogene: wat is het? & Hoe beïnvloedt het de celcyclus?
Oncogene: wat is het? & Hoe beïnvloedt het de celcyclus?  Wat zijn de overeenkomsten die metalen en niet-metalen gemeen hebben?
Wat zijn de overeenkomsten die metalen en niet-metalen gemeen hebben?  Nieuwe bevindingen beschrijven een methode om de innerlijke werking van sterren in een zeldzame fase te onderzoeken
Nieuwe bevindingen beschrijven een methode om de innerlijke werking van sterren in een zeldzame fase te onderzoeken Brits stadsbos kan evenveel koolstof opslaan als tropische regenwouden
Brits stadsbos kan evenveel koolstof opslaan als tropische regenwouden
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

