
Wetenschap
Een nieuwe oplosser voor geschatte marginale kaartinferentie
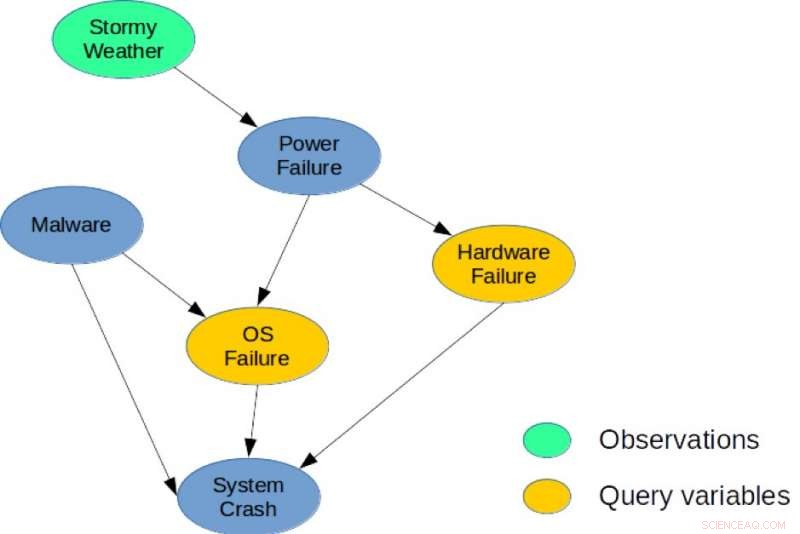
Figuur 1. Een eenvoudig Bayesiaans netwerk voor een systeemdiagnosetaak. Krediet:IBM
Er is een diep verband tussen planning en gevolgtrekking, en in het afgelopen decennium, meerdere onderzoekers hebben expliciete reducties geïntroduceerd die laten zien hoe stochastische planning kan worden opgelost met behulp van probabilistische gevolgtrekking met toepassingen in robotica, het roosteren, en milieuproblemen. Echter, heuristische methoden en zoeken zijn nog steeds de best presterende benaderingen voor planning in grote combinatorische toestands- en actieruimten. Mijn co-auteurs en ik kiezen voor een nieuwe benadering in onze paper, "Van stochastische planning tot marginale MAP" (auteurs:Hao Cui, Radu Marinescu, Roni Chardon), op de 2018 Conference on Neural Information Processing Systems (NeurIPS) door te laten zien hoe ideeën uit de planning kunnen worden gebruikt voor gevolgtrekking.
We ontwikkelden de Algebraic Gradient-based Solver (AGS), een nieuwe oplosser voor geschatte marginale MAP-inferentie. Het algoritme bouwt een benaderende algebraïsche berekeningsgrafiek die marginalen van toestands- en beloningsvariabelen vastlegt onder onafhankelijkheidsaannames. Vervolgens gebruikt het automatische differentiatie en zoeken op basis van gradiënten om de actiekeuze te optimaliseren. Onze analyse toont aan dat de waarde berekend door de AGS-berekeningsgrafiek identiek is aan de oplossing van Belief Propagation (BP) wanneer deze wordt geconditioneerd op acties. Dit zorgt voor een expliciet verband tussen heuristische planningsalgoritmen en benaderende gevolgtrekkingen.
Specifieker, we bekijken het verband tussen stochastische planning en probabilistische gevolgtrekking opnieuw. We stellen voor om voor het eerst een efficiënt heuristisch algoritme te gebruiken dat oorspronkelijk was ontworpen voor het oplossen van planningsproblemen om een centrale inferentietaak voor probabilistische grafische modellen aan te pakken, namelijk de marginale maximale a posteriori kans (MMAP) taak.
Probabilistische grafische modellen zoals Bayesiaanse netwerken of Markov-netwerken bieden een zeer krachtig raamwerk om te redeneren over voorwaardelijke afhankelijkheidsstructuren over veel variabelen. Voor dergelijke modellen is de MMAP-afleidingsquery is een bijzonder moeilijke maar belangrijke taak, overeenkomend met het vinden van de meest waarschijnlijke configuratie (of het maximaliseren van de waarschijnlijkheid) over een subset van variabelen, MAP-variabelen genoemd, na het marginaliseren (of optellen) van de rest van het model.
MMAP-inferentie komt in veel situaties voor, vooral bij diagnose- en planningstaken, waarin de meest natuurlijke specificatie van het model veel variabelen bevat waarvan we de waarden niet belangrijk vinden om te voorspellen, maar die onderlinge afhankelijkheid creëren tussen de variabelen van belang. Bijvoorbeeld, in een modelgebaseerde diagnosetaak, gegeven waarnemingen, we proberen te optimaliseren over een subset van diagnosevariabelen die potentieel falende componenten in een systeem vertegenwoordigen.
Ter illustratie, overweeg het Bayesiaanse netwerk getoond in figuur 1, die een eenvoudig diagnoseprobleem voor een computersysteem weergeeft. Het model legt directe causale afhankelijkheden vast tussen zes willekeurige variabelen die worden gebruikt om dit probleem te beschrijven. specifiek, een systeemcrash kan worden veroorzaakt door een hardwarefout, een OS-fout, of de aanwezigheid van malware in het systeem. evenzo, een stroomstoring kan een veelvoorkomende oorzaak zijn van hardware- en OS-storingen, en stormachtig weer kan de stroomstoring veroorzaken. Een mogelijke MMAP-query zou zijn om de meest waarschijnlijke configuratie van hardware- en besturingssysteemstoringen te berekenen, gezien het feit dat we stormachtig weer observeren, ongeacht de status van de andere variabelen (malware, Systeem crash, of stroomstoring).
Stochastische planningskaders zoals Markov-beslissingsprocessen worden veel gebruikt om planningstaken onder onzekere omstandigheden te modelleren en op te lossen. Eindige horizonplanning kan worden vastgelegd met behulp van een dynamisch Bayesiaans netwerk (DBN) waarin toestands- en actievariabelen bij elke tijdstap expliciet worden weergegeven en de voorwaardelijke kansverdelingen van variabelen worden gegeven door de overgangskansen. Bij offline plannen, de taak is om een beleid te berekenen dat de beloning op lange termijn optimaliseert. In tegenstelling tot, bij online planning krijgen we een vaste beperkte tijd t per stap en kunnen we vooraf geen beleid berekenen. In plaats daarvan, gezien de huidige staat, het algoritme moet binnen tijd t beslissen over de volgende actie. Vervolgens wordt de actie uitgevoerd, een overgang en beloning worden waargenomen en het algoritme wordt gepresenteerd met de volgende status. Dit proces herhaalt zich en de langetermijnprestaties van het algoritme worden geëvalueerd.
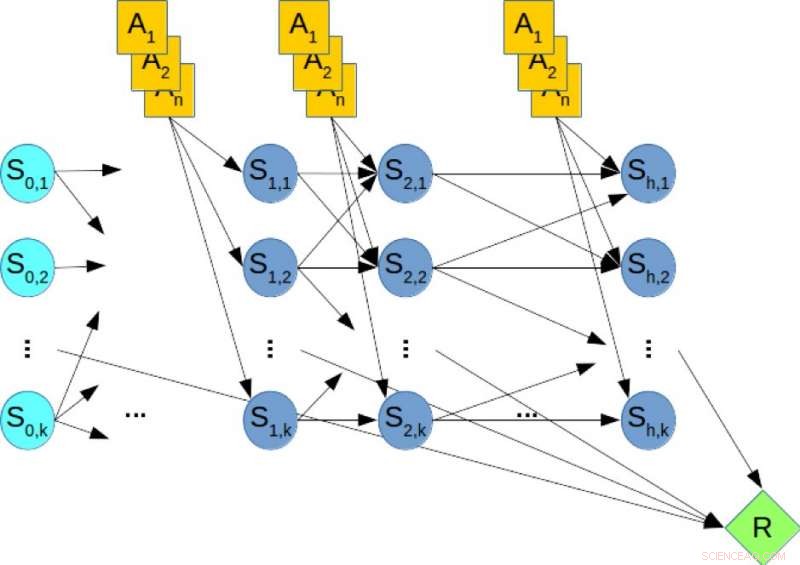
Figuur 2. Een dynamisch Bayesiaans netwerk (DBN) voor stochastische planning. Krediet:IBM
Ter illustratie, overweeg figuur 2, waaruit blijkt dat de DBN overeenkomt met een hypothetisch planningsprobleem, waarbij de oranje knooppunten de actievariabelen vertegenwoordigen, de blauwe knooppunten geven de toestandsvariabelen aan, en het groene knooppunt geeft de cumulatieve beloning aan die moet worden gemaximaliseerd. Daarom, het berekenen van het optimale beleid van het planningsprobleem is gelijk aan het oplossen van een MMAP-query over de DBN, waarbij we de actievariabelen maximaliseren en de toestandsvariabelen marginaliseren.
Onze experimentele evaluatie van moeilijke MMAP-probleemgevallen toont overtuigend aan dat het AGS-schema de prestaties van geavanceerde algoritmen op elk moment verbetert op MMAP-problemen met subproblemen met harde sommatie, soms tot één orde van grootte. Wij zijn van mening dat deze verbanden tussen planning en gevolgtrekking verder kunnen worden onderzocht om verbeteringen op beide gebieden op te leveren.
Dit verhaal is opnieuw gepubliceerd met dank aan IBM Research. Lees hier het originele verhaal.
 Wat zijn spider crickets?
Wat zijn spider crickets?  Is het tijd om de grenzen van het gebouwde omgevingsdenken te overschrijden?
Is het tijd om de grenzen van het gebouwde omgevingsdenken te overschrijden? Waar gaat onbehandeld afvalwater in ontwikkelingslanden naartoe?
Waar gaat onbehandeld afvalwater in ontwikkelingslanden naartoe? Hoe zijn reptielen belangrijk voor de mens?
Hoe zijn reptielen belangrijk voor de mens?  Redactioneel:De wereld had een klap nodig van de klimaatbijeenkomst in Madrid. Het kreeg in plaats daarvan een gejammer
Redactioneel:De wereld had een klap nodig van de klimaatbijeenkomst in Madrid. Het kreeg in plaats daarvan een gejammer
Hoofdlijnen
- Vrijgelaten zeeschildpad draagt as van oceanografen naar zee
- De celstructuur van een ui
- Tekenen van slaap gezien in kwallen
- Cladistics: Definitie, methode en voorbeelden
- Hoe is de katoenplant aangepast om te overleven?
- Duizenden pinguïnkuikens verhongeren op Antarctica
- Onverwachte vondst lost 40 jaar oud cytoskeletmysterie op
- Hoe duplicaten in twee rijen in OpenOffice te verwijderen
- Wetenschappers brengen nieuwe inzichten in de erfelijkheid van de ernst van de hiv-infectie
- Scheepsrampen vermeden met technieken voor big data-statistieken

- Facebook deelde gebruikersgegevens met geselecteerde bedrijven

- Vervanging van natuurlijke koudemiddelen kan de energiekosten verlagen en het milieu sparen

- Je kunt niet zien of een online restaurantrecensie nep is, maar deze AI kan dat wel
- New York City klaagt T-Mobile aan voor het bedriegen van klanten

 Klimaatberekeningen op lange termijn verbeteren
Klimaatberekeningen op lange termijn verbeteren Zelfs zonder het schone energieplan, VS kunnen emissiereducties in de Overeenkomst van Parijs bereiken
Zelfs zonder het schone energieplan, VS kunnen emissiereducties in de Overeenkomst van Parijs bereiken Onderzoek vindt omslagpunt voor grootschalige sociale verandering
Onderzoek vindt omslagpunt voor grootschalige sociale verandering Welk type bodem zijn diamanten in?
Welk type bodem zijn diamanten in?  De verborgen gevaren van antibioticaresistentiegenen in de lucht
De verborgen gevaren van antibioticaresistentiegenen in de lucht 267 miljoen mensen wereldwijd lopen gevaar door zeespiegelstijging
267 miljoen mensen wereldwijd lopen gevaar door zeespiegelstijging Risicoaversie neemt toe bij gewelddadige misdaad
Risicoaversie neemt toe bij gewelddadige misdaad Studie vindt oorzaak van visuele beperking bij astronauten
Studie vindt oorzaak van visuele beperking bij astronauten
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

